Логические задачи для 3 класса

Вместо заключения

Привлечение школьников в подобные викторины позволяет учителю продуктивнее строить уроки, вовлекать всех детей в игровой процесс обучения, повышать интерес к своему предмету и улучшать успеваемость учащихся. Дети могут самостоятельно придумывать вопросы к викторине и задавать их классу, команде или отдельным участникам. На основе наших вариантов вопросов вы тоже можете попытаться составить вопросы к викторине по математике с ответами для вашего класса. Надеемся, что материалы нашей статьи стали полезными для читателей, а педагоги с удовольствием воспользуются ими при организации подобного рода уроков.

Что поможет ребёнку решать задачи

В заключение расскажем о том, как сделать процесс решения задач проще и интереснее:

• Для того чтобы решать задачи, необходимо уметь считать. Следует выучить с ребёнком таблицу умножения, освоить примеры с дробями и простые уравнения.
• Чтобы решение задач не превратилось для ребёнка в рутину, проявите фантазию. Меняйте текст задания в соответствии с интересами ребёнка. Например, решать задачи на движение будет куда интереснее, если заменить банальные поезда трансформерами, летящими навстречу друг другу в эпической схватке. 
• Дети с развитой логикой учатся решать задачи быстрее. Советуем разбавлять чисто математические задания логическими. Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.   

<<Блок перелинковки>>

После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.

Избавление от знака модуля

Пусть нам дано уравнение $\left| f\left( x \right) \right|=a$, причём $a\ge 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:

\

Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого

\

Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:

\

Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.

Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:

\

Опять раскрываем модуль с плюсом и минусом:

\

Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.

Случай переменной правой части

А теперь рассмотрим вот такое уравнение:

\

Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.

Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.

А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».

Таким образом, сформулируем правило для произвольных функций $f\left( x \right)$ и $g\left( x \right)$ :

\

Применительно к нашему уравнению получим:

\

Ну, с требованием $2x\ge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.

Поэтому решим-ка само уравнение:

\

Ну и какой их этих двух корней удовлетворяет требованию $2x\ge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5}\;$. Вот и всё решение.:)

Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:

\

Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:

\

И решается оно точно так же:

\

С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:

\

Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:

\

Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:

\

\

Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.

Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:

\

Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:

\

\

Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3}\;$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:

\

Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:

\

Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:

\

Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.

Задача №5

Мудрецы и колпаки.

Царь решил проверить своих троих мудрецов на мудрость, пригласил их и сказал: «Мудрецы, у меня есть 5 колпаков – 3 из них черные, а 2 белые. Сейчас вы закроете глаза, и я надену на ваши головы эти колпаки, при этом вы не будете знать, колпак какого цвета у вас на голове, но будете видеть колпаки других мудрецов». После осуществленных действий мудрецы открыли глаза и долго-долго молчали. Затем один из мудрецов произнес: «На моей голове черный колпак!» И он был прав.

Вопрос: как мудрец догадался?

Ответ

После того, как мудрецы открыли глаза, они долго-долго молчали, что является ключевой фразой, потому что если бы один из мудрецов увидел на двух других белые колпаки, то он бы сразу понял, что на нем черный колпак. Поэтому первый важный вывод: на головах мудрецов нет двух белых колпаков. Соответственно, есть либо один белый, либо вообще нет.

Далее. Наши мудрецы: А, Б и В. Догадался о том, что на нем черный колпак мудрец А. Проследим ход его мыслей:

«Предположим на мне белый колпак, тогда мудрец Б, глядя на меня рассуждал бы так: «Возможно, на мне белый колпак, получается на мудреце А тоже белый колпак, тогда мудрец В сразу же сказал бы, что на нем черный колпак, но этого не происходит, значит на мне черный колпак», но ведь он не говорит, что на нем черный колпак! Значит, мое предположение неверно, и он не видит на мне белого колпака. Значит мой колпак черный!»

Да, такая вот интересная задача.

Помимо задач хотелось бы предложить загадки с подвохом. По возможности уделите время их решению, это будет увлекательно.

Примеры решений

Решение:

Пусть $x$ — количество монет в мешке, а значит в сундуке: $3x$ монет.
После того, как из мешка переложили $24$ монеты, в сундуке стало: $3x+24$, а в мешке $x-24$. И если в сундуке их стало в $7$ раз больше чем в мешке, то имеем: $3x+24=7(x-24)$.

Ну вот мы и составили уравнение (математическую модель), осталось решить уравнение относительно $x$ и записать ответ.

Решим полученное уравнение: $3x+24=7(x-24)$. Легко увидеть, что уравнение является линейным (узнать как решаются линейные уравнения можно тут.)

Раскроем скобки в правой части уравнения: $3x+24=7x-7\cdot 24$. Перенесём все слагаемые содержащие переменную в правую часть, а всё что не содержит $x$ в левую, получим: $24+7\cdot 24=7x-3x$. После упрощения получили $192=4x$, разделим обе части уравнения на коэффициент при неизвестном, т.е на $4$, тогда получим $x=48$.

Решение:

Пусть в первый мешок насыпали $3x$ кг муки, тогда во второй мешок насыпали $x$ кг. Если сложим количество кг в каждом мешке, то получим $3600$ кг муки. Имеем: $3x+x+800=3600$, решим уравнение классическим методом.

Все слагаемые содержащие $x$ оставим слева, а всё остальное перенесём в правую часть равенства: $3x+x=3600-800$, упростим обе части; $4x=2800$ поделим обе части равенства на $4$ и получим ответ: $x=700$.

Решение:

Пусть во втором мешке $x$ кг картофеля, тогда в первом мешке $4x$ кг. Из первого взяли $40$ кг, тогда в первом стало: $4x-40$. Во второй мешок насыпали $5$ кг и теперь в нём: $x+5$ кг картошки. Нам известно, что после этих изменений количество картофеля в мешках стало поровну, запишем это с помощью линейного уравнения:

$$4x-40=x+5$$

Решим это линейное уравнение. Все слагаемые содержащие переменную перенесём влево, а свободные члены вправо и получим:

$$4x-x=5+40$$

Упростим выражения:

$$3x=45$$

Избавимся от коэффициента при неизвестном и получим ответ:

$$x=15$$

Решение:

Пусть машины едут со скоростью $v$ км/ч, тогда после ускорения первой машины её скорость стала: $v+20$ км/ч, а скорость второй машины после замедления стала: $v-20$ км/ч. Нам известно по условию, что после изменения скоростей машин, первая проходит за два часа ровно столько, сколько вторая за четыре, тогда имеем:

По известной нам формуле $S=vt$ ($S$ — расстояние, $v$ — скорость, $t$ — время)

$$2(v+20)=4(v-20)$$

Сократим обе части равенства на $2$, тогда получим: $v+20=2(v-20)$. Раскроем скобки в правой части уравнения и сгруппируем все переменные в правой части равенства.

$$v+20=2v-2\cdot 20$$

$$v+20=2v-40$$

$$20+40=2v-v$$

$$v=60$$

Решение:

Пусть во вторую бригаду привезли $x$ кг раствора цемента, тогда в первую бригаду привезли $x-50$ кг. Через 3 часа работы у первой бригады осталось $x-50-3\cdot 150$ кг цемента, а у второй $x-3\cdot 200$ кг.

По условию известно, что через 3 часа работы в первой бригаде осталось в 1,5 раза больше цемента, чем во второй, тогда имеем:

$$x-50-3\cdot 150=1,5(x-3\cdot 200)$$

Осталось решить данное уравнение относительно $x$ и истолковать ответ.

Упростим и раскроем скобки в правой части, тогда получим:

$$x-500=1,5x-1,5\cdot 600$$

Если вам неудобно работать с десятичными дробями, то вы всегда можете их переводить в рациональный вид: $1,5=\frac{15}{10}=\frac{3}{2}$.

Запишем с учётом перевода дробей и упростим:

$$x-500=\frac{3}{2}x-\frac{3}{2}\cdot \frac{600}{1}$$

$$x-500=\frac{3x}{2}-\frac{3}{1}\cdot \frac{300}{1}$$

$$x-500=\frac{3x}{2}-900$$

Перенесём слагаемые содержащие переменную в правую сторону, а всё остальное в левую:

$$900-500=\frac{3x}{2}-x$$

$$400=\frac{3x}{2}-\frac{x}{1}$$

$$400=\frac{3x-2x}{2}$$

$$400=\frac{x}{2}$$

Домножим обе части на 2 и получим ответ:

$$x=800$$

Основная формула

Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?

Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:

\

Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:

\

А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $\left| -3 \right|=3$, т.е. требуемое равенство выполняется.

Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $\left| x \right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.

Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $f\left( x \right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:

\

Ну и как такое решать? Напомню: $f\left( x \right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:

\

или:

\

Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет

Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.

А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$\left| 2x+1 \right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $\left| 2x+1 \right|=-\left( 2x+1 \right)=-2x-1$. В первом случае наше уравнение перепишется так:

\

И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:

\

Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.

Теперь разберём случай отрицательного подмодульного выражения:

\

Опа! Снова всё чётко: мы предположили, что $2x+1 \lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:

\

Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $\left| x \right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?

Да, такой алгоритм существует. И сейчас мы его разберём.

Задача №1

Представьте, перед вами четыре стакана, наполненных водой. В каждом стакане находятся предметы. Так:

• в первом стакане – металлические наручные часы;
• во втором стакане – канцелярская скрепка;
• в третьем стакане – металлические ножницы;
• в четвертом стакане – ластик.

При этом уровень воды во всех стаканах одинаковый. Визуально это выглядит следующим образом:

Вопрос: в каком стакане воды больше, чем в остальных?

Ответ

Во втором стакане. Все дело в скрепке, которая по сравнению с другими предметами имеет меньший объём. Соответственно, для необходимого уровня воды требуется больше.

Размялись? Согласитесь, это было несложно. Продолжаем…

Математические задачи на логику для дошкольников

Начиная с 3 летнего возраста малыша, родители должны понемногу заниматься тренировкой логического мышления у своих детей

Детям это очень важно, ведь для них в таком возрасте многие очевидные вещи кажутся сложными, а непонятные для восприятия взрослым, напротив, очевидными. Представим несколько вариантов логических задач для детей 3-5 лет

1. На столе лежит 1 апельсин. Его разрезали на 2 части, сколько апельсинов лежит на столе? Ответ: 1, разрезанный.
2. Собаку привязали к забору веревкой. Длина веревки составляет 10 метров, а собака прошла за день 100 метров. Как ей это удалось? Ответ: Собака ходила вдоль забора туда и обратно и «находила» целых 100 метров.

3. Какой день недели соответствует числу 3? Ответ: среда, т.к. его порядковый номер в неделе – 3.

   Примечание: Про дни недели дошкольникам можно задавать различные варианты вопросов. Это поможет не только в развитии логического мышления, но и поможет скорее выучить дни недели.

4. Посчитать, сколько людей в следующей строке: ты да я, да мы с тобой. Ответ: 2.
5. Папа и сын, дедушка и внук, сын и папа. Сколько всего человек здесь отмечено? Ответ: 3, т.к. папа – сын дедушки, сын папы – внук дедушки.
6. На опушке стояло 3 высоких сосны. На каждой сосне по 3 больших ветки и по 3 маленьких. На каждой маленькой ветке по яблоку. Сколько всего яблок на деревьях? Ответ: 0, на соснах яблоки не растут.
7. Папу Антона зовут Андрей Викторович, а дедушку – Сергей Иванович. Какое отчество у мамы Антона? Ответ: Сергеевна, Потому что Сергей Иванович – это отец мамы Антона. Отца папы Антона зовут Виктор.
8. У двух братьев по одной сестре. Сколько всего детей в семье? Ответ: 3. 2 брата и одна сестра на двоих.

9. Какие камни есть в море? Ответ: мокрые.

   Примечание: аналогичная задача-загадка моет звучать так «Каких камней в море нет?» — ответ: сухих.

10. Вася и Петя играли в морской бой и сыграли по 3 партии. Каждый выиграл по 3 раза. Это правда или ложь? Ответ: ложь. Во время одной партии выиграть может только один.
11. В поле работали 5 тракторов. 2 трактора сломались и остановились. Сколько тракторов в поле? Ответ: 5, т.к. учитываются все тракторы, и рабочие, и сломанные.
12. Одно яйцо варится 5 минут. Сколько времени нужно, чтобы сварить 2 яйца? Ответ: все те же 5 минут.
13. Саша сидит в самолете. Впереди него машина, сзади – лошадь. Где находится Саша? Ответ: катается на карусели.
14. Алена сидит, когда она встанет и уйдет, ее мама так и не сможет сесть на ее место. Где сидит Алена? Ответ: у мамы на коленях.
15. Что все дети на земле делают одновременно? Ответ: взрослеют.

Опираясь на предложенные варианты заданий на развитие логического мышления, родители могут придумывать незамысловатые условия задач самостоятельно.

Задача №2

Давайте немного вспомним арифметические действия и применим их к задаче.

В кафе быстрого питания зашли четыре посетителя. При этом:

• первый посетитель купил три бургера и заплатил 300 рублей;
• второй посетитель купил один бургер и две порции картофеля фри и заплатил 200 рублей;
• третий посетитель купил два куска пиццы и одну порцию картофеля фри и заплатил 90 рублей;
• четвертый посетитель купил один бургер, одну порцию картофеля фри и один кусок пиццы.

Схематично эту ситуацию можно представить так:

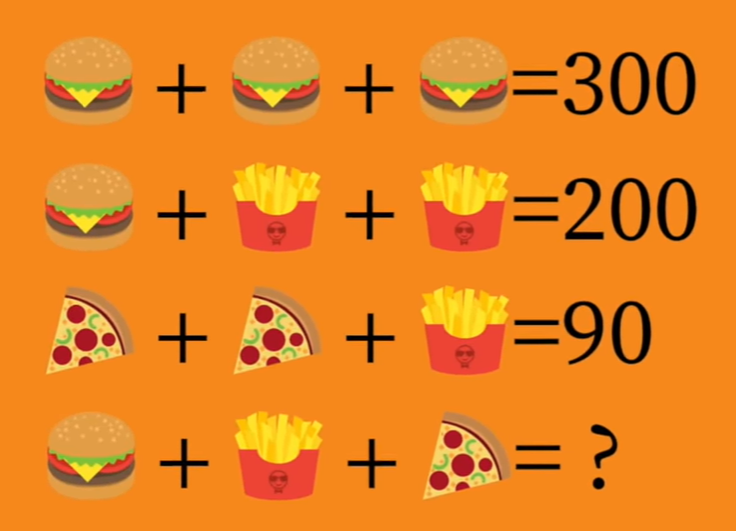
Вопрос: сколько заплатил четвертый посетитель?

Ответ

Если три бургера составили 300 рублей, то один бургер стоит 100 рублей (300/3). Если второй посетитель заплатил 100 рублей за бургер, то еще 100 рублей приходится на две порции картофеля, то есть одна порция картофеля фри стоит 50 рублей (100/2). Если третий посетитель заплатил 90 рублей, потратив 50 рублей на картофель, а сорок рублей на две пиццы, то одна пицца стоит 20 рублей (40/2). Соответственно четвертый посетитель заплатил: 100 + 50 + 20 = 170 рублей.

Блок «Юные математики»

В этом блоке собраны вопросы-задачи, для ответа на которые придется совершать математические действия. В каком формате проводить этот блок, решает учитель. Можно давать задания всей команде или вызывать попарно участников для решения задачи на доске или листочке. Приводим варианты возможных вопросов с ответами.

1. К светофору подъехали: БМВ, Ауди, Фольксваген. В какой последовательности они остановились, если Фольксваген – не первый, а Ауди – не третья и не первая? (правильный ответ – БМВ, Ауди, Фольксваген)
2. Для игры в ручеек дети разбились по парам. Маша увидела три пары слева и восемь пар справа, сколько детей принимает участие в игре? (правильный ответ – 24 ребенка)
3. В бассейне 16 тонн воды. Из него откачали 5 тонн. Сколько тонн воды нужно долить, чтобы в бассейне стало 36 тонн воды? (правильный ответ – 21 тонну)
4. В корзинке сидят десять щенков. Сколько корзин еще нужно взять чтобы рассадить по двое в каждую? (правильный ответ – четыре)
5. На сколько изменится количество ручек, если взять два раза по десять, а положить обратно четыре раза по пять? (правильный ответ – ничего не изменится)
6. Марине родители дали 150 рублей, а Вике в два раза больше. Что нужно сделать Вике чтобы у них стало одинаковое количество денег? (правильный ответ – отдать Маше 75 рублей)
7. Конфета стоит 13 рублей, как расплатиться, если у покупателя только пятирублевые монеты, а у кассира только двухрублевые? (правильный ответ – дать 3 монеты и получить одну сдачи)
8. Из пункта A в пункт B выехали пять машин. Они проехали 200 километров. Какое расстояние проехала каждая из них? (правильный ответ – 40 км.)
9. Кувшин сока весит 2,5 килограмма. Когда половину сока выпили он стал весить 1.5 килограмм. Сколько весит кувшин? (правильный ответ – 500 грамм)
10. За два часа дети съедают двенадцать килограмм торта. Сколько сладкого они съедят за двадцать минут? (правильный ответ – 4 килограмма)
11. У Маши было 5 листочков картона, некоторые из них она разрезала пополам так, что получилось 9. Сколько листов разрезала Маша? (правильный ответ – 4 листа)
12. На столе стоит четыре вазочки с конфетами. Дети съели одну вазочку сладкого и поставили ее обратно. Сколько вазочек стоит на столе? (правильный ответ – четыре)
13. Чемодан весит больше сумки на один килограмм. Сколько весит полный чемодан, если масса сумки с аналогичным содержимым – три килограмма? (правильный ответ – 4 килограмма)
14. Три футбольные команды участвуют в турнире. Каждая из них играет один матч с двумя другими. Сколько игр будет сыграно? (правильный ответ – три игры)
15. В поезде было семь свободных купе. На станции зашло 12 человек. Сколько свободных купе осталось? (правильный ответ – 4 купе)
16. Петя нарисовал две прямые линии, на одной поставил две точки, а на другой три. Общее число точек оказалось равным четырем. Как такое возможно? (правильный ответ – линии пересекаются)
17. Кекс стоит дешевле пирожного, но дороже кусочка торта. Что дешевле пирожное или кусочек торта? (правильный ответ – кусочек торта)
18. В двух комнатах пятьдесят кресел. Из одной из них вынесли десять кресел, и в обеих комнатах количество кресел сравнялось. Сколько посадочных мест было в каждой комнате? (правильный ответ – двадцать в одном и тридцать во втором)
19. Гуляя по лесу, Петя увидел ручеек. Он шел по правому берегу, но три раза перепрыгивал его. На каком берегу в конечном итоге оказался мальчик? (правильный ответ – на левом берегу)
20. Во дворе играют 11 мальчиков и 15 девочек. Сколько детей должно присоединиться чтобы можно было разделиться на 8 равных команд? (правильный ответ – 6 человек)

Тест «Порядок арифметических действий» 4 класс – Математика 4 класс – 4 класс

3 4 6 5 1 2 б) 320 : 8 х 7 + 9 х ( 240 – 60:15) 5. В каком из выражений последнее действие умножение? а) 1001 :13 х (318 +466) :22 б) 391 х37 :17 х (2248:8 – 162) в) 10000 – (5 х 9+56 х 7) х2 6. В каком из выражений первое действие вычитание? а) 2025 :5 – ( 524 – 24 :6) х45 б) 5870 + ( 90-50 +30) х8 -90 в) 5400 :60 х (3600:90 -90)х5 7. Выбери верное высказывание: «В выражении без скобок действия выполняются:» а) по порядку б) х и : , затем + и – в) + и -, затем х и : 8. Выбери верное высказывание: «В выражении со скобками действия выполняются:» а) сначала в скобках б)х и :, затем + и – в) по порядку записи Выбери верный ответ: 9. 90 – ( 50- 40:5) х 2+ 30 а) 56 б) 92 в) 36 10. 100- (2х5+6 – 4х4) х2 а) 100 б) 200 в) 60 11. ( 10000+10000:100 +400) : 100 +100 а) 106 б) 205 в) 0 12. 150 : ( 80 – 60 :2) х 3 а) 9 б) 45 в) 1

Тест «Порядок арифметических действий» 1(1б) 2(1б) 3(1б) 4(3б) 5(2б) 6(2б) 7(1б) 8(1б) 9(3б) 10(3б) 11(3б) 12(3б) 1. Какое действие в выражении сделаешь первым? 560 – (80+20) :10 х7 а) сложение б) деление в) вычитание 2. Какое действие в этом же выражении сделаешь вторым? а) вычитание б) деление в) умножение 3. Выбери правильный вариант ответа данного выражения: а) 800 б) 490 в) 30 4. Выбери верный вариант расстановки действий: а) 3 4 6 5 2 1 4 5 6 3 2 1 320 : 8 х 7 + 9 х ( 240 – 60:15) в) 320:8 х 7+9х(240 – 60 :15)

3 4 6 5 2 1 б) 320 : 8 х 7 + 9 х ( 240 – 60:15) 5. В каком из выражений последнее действие деление? а) 1001 :13 х (318 +466) :22 б) 391 х37 :17 х (2248:8 – 162) в) 10000 – (5 х 9+56 х 7) х2 6. В каком из выражений первое действие сложение? а) 2025 :5 – ( 524 + 24 х6) х45 б) 5870 + ( 90-50 +30) х8 -90 в) 5400 :60 х (3600:90 -90)х5 7. Выбери верное высказывание: «В выражении без скобок действия выполняются:» а) по порядку б) х и : , затем + и – в) + и -, затем х и : 8. Выбери верное высказывание: «В выражении со скобками действия выполняются:» а) сначала в скобках б)х и :, затем + и – в) по порядку записи Выбери верный ответ: 9. 120 – ( 50- 10:2) х 2+ 30 а) 56 б) 0 в) 60 10. 600- (2х5+8 – 4х4) х2 а) 596 б) 1192 в) 60 11. ( 20+20000:2000 +30) : 20 +200 а) 106 б) 203 в) 0 12. 160 : ( 80 – 80 :2) х 3 а) 120 б) 0 в) 1

Блок «Капитанский конкурс»

Каждому капитану дается на решение одна из предложенных задач. Побеждает тот, кто решит ее быстрее других и правильно.

1. На витрине цветочного магазина стоит четыре вазы с цветами. В каждой из них цветы определенного вида: розы, васильки, хризантемы и ромашки. Бабочка садится на букет не более одного раза. Сначала она садится на розы, но с хризантем на ромашки сразу она не перелетает. Сколькими способами бабочка может попить нектар со всех цветов? (правильный ответ – четырьмя)
2. Петя с Леней прошли в финальный этап турнира по шахматам. Перед финалом они решили, что победитель получит пять очков, тот кто проиграет ничего не получит, а в случае ничьи каждый из них получит по два очка. Финал состоял из тринадцати игр и в сумме они набрали 60 очков. Количество очков Пети за выигранные им партии оказалось в три раза больше, чем за сыгранные в ничью. В каком количестве игр победу одержал Леня? (правильный ответ – в двух)
3. Из книги выпало несколько страниц, первая из которых имеет номер 14, а номер последней – из тех же цифр, но в обратном порядке. Сколько страниц выпало из книги? (правильный ответ – 27 страниц)
4. Из емкости взяли 21 ковшик воды, затем долили 24 ковшика и там стало 43 ковшика воды. Сколько ковшиков там было изначально? (правильный ответ – 40 ковшиков)
5. Скорость ласточки составляет десять метров в секунду. Какое расстояние в километрах она пролетит за один час? (правильный ответ – 36 километров)

Немного теории

Итак, поехали

Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $\left| -5 \right|=5$

Или $\left| -129,5 \right|=129,5$.

Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $\left| 5 \right|=5$; $\left| 129,5 \right|=129,5$ и т.д.

Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $\left| -5 \right|=\left| 5 \right|=5$; $\left| -129,5 \right|=\left| 129,5 \right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:

\

Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.

Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:

\

Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.

Таким образом, если рассмотреть функцию $y=\left| x \right|$ и попробовать нарисовать её график, то получится вот такая «галка»:

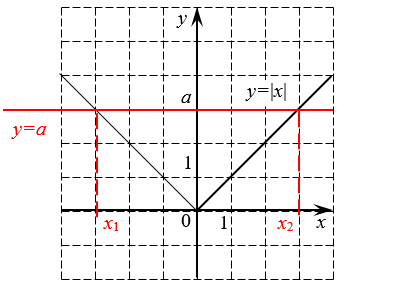График модуля и пример решения уравнения

Из этой картинки сразу видно, что $\left| -m \right|=\left| m \right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)

Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $\left| {{x}_{1}}-{{x}_{2}} \right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:

Модуль — это расстояние между точками на числовой прямой

Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)

Порядок вычисления простых выражений

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7−3+6.

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7−3+6=4+6=10

Ответ: 7−3+6=10.

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 62·83?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17−5·63−2+42.

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке слева направо. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:

17−5·63−2+42=17−10−2+2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17−10−2+2=7−2+2=5+2=7

Ответ: 17−5·63−2+42=7.

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Математика 4 класс. Задачи, решения, ответы.

Задачи по математике 4 класс.

Задание 1:

В магазин привезли 32 коробки конфет, по 9 кг в каждой, и 36 коробок вафель, по 8 кг в каждой. Каких сладостей привезли больше и на сколько килограммов больше?

Решение:1) 32 * 9 = 288 2) 36 * 8 = 288
Ответ: В магазин привезли одинаковое количество конфет и вафель.

Задание 2:

С одного поля собрали 1 т 800 кг картофеля, а с другого — в 3 раза меньше. Весь картофель разложили в мешки, по 40 кг в каждый. Сколько мешков с картофелем получили?

Решение:1)1800 : 3 = 600 (со второго поля) 2) 1800 + 600 = 2400 (всего собрали картофеля) 3) 2400 : 40 = 60(мешков с картофелем получили)
Ответ: 60 мешков.

Задание 3:

• 1) Вычисли периметр и площадь прямоугольника со сторонами 2 см и 4 см.
• 2) Найди длину стороны квадрата, периметр которого равен периметру прямоугольника в задании 1).

Решение:1) 2 + 2 + 4 + 4 = 12 см (периметр прямоугольника), 2 * 4 = 8 квадратных сантиметра
2) 12 : 4 = 3 (длина стороны квадрата)

Задание 4:

Один мастер изготовил 6 ниток бус, по 38 бусинок в каждой, а другой — 7 ниток бус, по 36 бусинок в каждой. Какой мастер использовал больше бусинок и на сколько?

Решение:1) 6 * 38 = 228 (бусинки использовал 1 мастер) 2) 7 * 36 = 252 (бусинки использовал 2 мастер) 3) 252 — 228 = 24
Ответ: Второй мастер использовал на 24 бусинки больше чем первый.

Задание 5:

В первый день в санаторий приехало 900 человек, а во второй — в 9 раз меньше, чем в первый. Всех отдыхающих поселили в комнаты, по 2 человека в каждой. Сколько комнат заняли все отдыхающие?

Решение:1) 900 : 9 = 100 (отдыхающих приехало во второй день) 2) 900 + 100 = 1000 (отдыхающих приехало за 2 дня) 3) 1000 : 2 = 500 (комнат заняли все отдыхающие) Ответ: 500 комнат.

Задание 6:

• 1) Вычисли периметр и площадь прямоугольника со сторонами 7 см и 3 см.
• 2) Найди длину стороны квадрата, периметр которого равен периметру прямоугольника в № 1).

Решение:1) 7 + 7 + 3 + 3 = 20 см (периметр), 7 * 3 = 21 см квадратных (площадь)
2) 20 : 4 = 5(длина стороны квадрата)
Задачи повышенной сложности по математике 4 класс.

Задание 1:

Один токарь за смену изготовил 32 детали. Другой токарь, работая с той же производительностью, изготовил 24 детали. Сколько часов работал первый токарь, если известно, что второй токарь работал на 2 часа меньше, чем первый?

Решение:

Пусть первый токарь работал x часов. Тогда второй токарь работал (x — 2) часов. Первый токарь за час изготавливал (32/x) деталей, а второй токарь (24/(x — 2)). По условию задачи оба токаря работали с одинаковой производительностью. Это значит, что за 1 час они изготавливали одинаковое число деталей, поэтому мы можем записать и решить уравнение: 30/x = 24/(x — 2); 32*(x — 2) = 24 * x; 32x — 64 = 24x; 8x = 64; x = 8.Ответ: первый токарь работал 8 часов.

Задание 2:

Сложная задача по математике для 4 класса: Из двух городов по реке одновременно выплыли навстречу друг другу две моторные лодки. Скорость первой лодки 15км/ч, второй лодки 35км/ч. Первая лодка двигалась по течению реки. Скорость течения реки 5км/ч. Через сколько часов лодки встретились, если расстояние между городами 250км?

Решение:

Пусть до встречи лодок первая проплыла x км. Тогда вторая лодка проплыла (250 — x) км. Учитывая скорость течения реки, скорость первой лодки 15 + 5 = 20км/ч. Соответственно, скорость второй лодки 35 — 5 = 30км/ч. Очевидно, что время в пути до встречи одинаково, поэтому можно записать уравнение: x/20 = (250 — x)/30; x * 30 = 20 * (250 — x); 30x = 5000 — 20x; 50x = 5000; x = 100км.

Первая лодка до встречи со второй прошла 100км. Рассчитаем время: t = x/20 = 100/20 = 5ч.

Для проверки мы можем рассчитать время второй лодки: t = x/20 = (250 — x)/30 = 150/30 = 5ч. Ответ: лодки встретились через 5 часов.

Задания по математике 4 класс:

Тест 1       |       Тест 2       |       Тест 3       |       Тест 4       |       Тест 5