Вычитание и сложение.
Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
Минус на минус даёт плюс
– это правило, которые мы выучили в школе и применяем всю жизнь. А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
С древних времён люди пользуются положительными натуральными числами: 1, 2, 3, 4, 5,… С помощью чисел считали скот, урожай, врагов и т.д. При сложении и умножении двух положительных чисел получали всегда положительное число, при делении одних величин на другие не всегда получали натуральные числа – так появились дробные числа. Что же с вычитанием? С детских лет мы знаем, что лучше к большему прибавить меньшее и из большего вычесть меньшее, при этом мы опять же не используем отрицательные числа. Получается, если у меня есть 10 яблок, я могу отдать кому-то только меньше 10 или 10. Я никак не смогу отдать 13 яблок, потому что у меня их нет. Нужды в отрицательных числах не было долгое время.
Только с VII века н.э.
отрицательные числа использовались в некоторых счётных системах, как вспомогательные величины, которые позволяли получить положительное число в ответе.
Рассмотрим пример
, 6х – 30 = 3х – 9. Чтобы найти ответ, необходимо члены с неизвестными оставить в левой части, а остальные — в правую: 6х – 3х = 30 – 9, 3х = 21, х = 7. При решении этого уравнения нам даже не встретились отрицательные числа. Мы могли бы члены с неизвестными перенести в правую часть, а без неизвестных — в левую: 9 – 30 = 3х – 6х, (-21) = (-3х). При деление отрицательного числа на отрицательное получаем положительный ответ: х = 7.
Что мы видим?
Действия с использованием отрицательных чисел должны привести нас к такому же ответу, что и действия только с положительными числами. Мы можем больше не думать о практической непригодности и осмысленности действий – они помогают нам решить задачу гораздо быстрее, не приводя уравнение к виду только с положительными числами. В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.
Со временем, после проведения длительных опытов и вычислений удалось выявить правила, которым подчиняются все числа и действия над ними (в математике они называются аксиомами). Отсюда и появилась аксиома, которая утверждает, что при умножении двух отрицательных чисел получаем положительное.
www.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
Топ вопросов за вчера в категории Математика
Математика 10.11.2023 08:28 4156 Крупнова Алёна
В магазине было 12 упаковок тетрадей в линейку, по 50 штук в каждой. За день продали 9 упаковок
Ответов: 2
Математика 15.06.2023 22:23 64553 Степовой Влад
Для инфузии медсестра использует капельницу, которая дозирует 20 капель на 1 мл раствора. Сколько
Ответов: 1
Математика 10.07.2023 13:55 1347 Котик Ксения
Составьте для каждого из слов свое множество «электричество», «учебник». Найдите пересечение и
Ответов: 2
Математика 03.06.2023 20:15 635 Дербаремдикер Даня
Ответов: 2
Математика 19.06.2023 07:55 145 Огорельцев Илья
Из 150 девятиклассников школы 30 человек приняли участие в математической олимпиаде. Сколько
Ответов: 2
Математика 09.07.2023 20:35 1818 Візер Андрій
Найдите среднее арифметическое, размах, моду и медиану ряда чисел: 3,8; 4,7; 1,7; 3,8; 2,3. Очень
Ответов: 2
Математика 12.06.2023 21:47 210 Мяус Юля
Какова концентрация полученного русалкой раствора, если она взяла соли в 5.4 раза меньше, чем
Ответов: 2
Математика 28.09.2023 06:29 525 Достоевская Полина
Бутылку налили 3л лимонада. Какой объем у бутылки,если лимонадом заполнили 6/7 её объёма
Ответов: 2
Математика 18.06.2023 09:41 152 Сургутская Кристина
На острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Однажды 35
Ответов: 2
Математика 12.06.2023 08:32 177 Пищаев Глеб
1. a) Составь краткую запись к задаче. Реши задачу. На школьном стадионе в футбол играли 22
Ответов: 3
Скобка в скобке
Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).
Чтобы успешно решать подобные задания, нужно:
— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.
При этом важно при раскрытии одной из скобок не трогать все остальное выражение, просто переписывая его как есть.
Давайте для примера разберем написанное выше задание.
Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).Решение:
|
\(7x+2(5\)\(-(3x+y)\)\()=\) |
Выполнять задание начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относиться – это сама скобка и минус перед ней (выделено зеленым). Всё остальное (не выделенное) переписываем также как было. |
|
| \(=7x+2(5\)\(-3x-y\)\()=\) |
Теперь раскрываем вторую скобку, внешнюю. |
|
| \(=7x+2·5-2·3x-2·y=\) |
Упрощаем получившееся выражение… |
|
|
\(=7x+10-6x-2y=\) |
…и приводим подобные. |
|
|
\(=x+10-2y\) |
Готово. |
Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).Решение:
|
\(-(x+3(2x-1\)\(+(x-5)\)\())\) |
Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается. |
|
|
\(-(x+3(2x-1\)\(+x-5\)\())\) |
Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке. |
|
|
\(=-(x\)\(+3(3x-6)\)\()=\) |
Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него. |
|
|
\(=-(x\)\(+9x-18\)\()=\) |
Вновь приводим подобные. |
|
|
\(=-(10x-18)=\) |
И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные. |
|
|
\(=-10x+18\) |
Готово. |
Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.
Умножение и деление
Многие люди знают, что умножение двух положительных чисел даёт положительное число. Например, 2 умножить на 3 даёт 6.
Но что происходит при умножении или делении чисел со знаком минус? При умножении числа на минус один (-1), результат будет противоположным по знаку. Например, -2 умножить на -1 даёт 2. Это объясняется тем, что умножение на минус один можно рассматривать как смену знака числа.
А что происходит при умножении или делении двух чисел со знаком минус? В данном случае, произведение или частное будет положительным числом. Например, -2 умножить на -3 даёт 6. Это можно интерпретировать так: два отрицательных числа, умноженные друг на друга, дают положительный результат.
Таким образом, можно сделать вывод, что при умножении или делении чисел со знаком минус, результат будет положительным числом. Это правило можно запомнить как «минус на минус даёт плюс».
Произведение отрицательных чисел
Минус на минус даёт плюс
В математике существует правило, которое гласит, что произведение двух отрицательных чисел равно положительному числу. Это правило иногда вызывает путаницу у учащихся, но его можно объяснить простыми словами.
Когда мы умножаем два отрицательных числа, мы фактически находим сумму отрицательных чисел. Например, если у нас есть -2 и -3, умножение их будет эквивалентно сложению: -2 + -2 + -2 = -6. Из этого примера видно, что произведение отрицательных чисел действительно может быть отрицательным числом.
Однако, когда мы умножаем два отрицательных числа друг на друга, мы получаем ситуацию, где минусы «неоднократно» складываются. То есть, каждый раз при умножении мы добавляем множитель минусов, и они сокращаются, в результате чего мы получаем положительное число. Например, (-2) * (-3) = 2 + 2 + 2 = 6.
Это можно представить в виде простой аналогии. Представьте, что у вас есть две группы людей, каждая из которых состоит из отрицательного числа людей. Когда они объединяются, каждая группа, как отрицательное число людей, образует некоторую силу, которая направлена внутрь, к минусовым значениям. Однако, когда группы объединяются, их силы складываются, но сами группы исчезают. В результате, получается положительная сила.
Таким образом, минус на минус действительно даёт плюс, и это правило является основой для дальнейших математических выкладок и рассуждений.
Частное отрицательных чисел
Почему на минусе на минусе получается плюс? Ответ на этот вопрос связан с особенностями математических операций с отрицательными числами. Когда мы вычитаем или делаем частное отрицательных чисел, мы в действительности складываем или умножаем на соответствующее положительное число.
Поскольку отрицательное число означает противоположность положительного, вычитание двух отрицательных чисел эквивалентно сложению положительного числа. То есть, -2 — (-3) можно переписать как -2 + 3, что равно 1. Таким образом, на минусе на минусе получается плюс.
То же самое относится и к делению отрицательных чисел. Если мы делим -6 на -2, то это можно переписать как -6 / (-2), что равно 3. И снова получается плюс.
Эта особенность происходит из логической связи между отрицательными числами и операциями сложения и умножения. При вычитании и делении отрицательных чисел мы фактически изменяем знак одного из чисел и выполняем операцию с положительными числами.
Умножение и деление двух чисел со знаком «-»
Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.
Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.
(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.
Вспомная о правилах работы со скобками, получаем:
1) (-C) х (-V) + (C х V) + (-C) х V = D;
2) (-C) х ((-V) + V) + C х V = D;
3) (-C) х 0 + C х V = D;
Из этого следует, что C х V = (-C) х (-V).
базовых математических символов | Словарь
математика (BrE) | математика (AmE) является сокращенной формой математика
На этой странице перечислены основные математические символы с их названиями и примерами на английском языке.
+ плюс/дополнение
Знак плюс
означает:
а.

положительное
Любое число больше нуля является положительным числом и может быть записано со знаком плюс или без него.
Таким образом, +5 (плюс пять) и 5 (пять) — одно и то же число.
б. операция сложения
3 + 5 = 8 три плюс пять равно восьми пять прибавить к трем, получится восемь три прибавить к пяти, получится восемь
Сложение дает нам сумму . В 3 + 5 = 8 сумма равна восьми.
—
знак минус/знак вычитания
Знак минус означает:
Любое число меньше нуля является отрицательным числом и записывается со знаком минус перед ним.
-3 минус три
б. операция вычитания
8 — 5 = 3 восемь минус пять равно трем пять вычесть из восьми равно трем если из восьми вычесть пять, то получится три если из восьми вычесть пять, то получится три
Вычитание дает нам разницы .
В 8 — 5 = 3 разница три.
×
знак умножения / знак умножения
Знак умножения на означает:
умножение
5 x 6 = 30 пять раз шесть равно тридцати пять умножить на шесть равно тридцати пять шестерок равно тридцати если умножить 5 на 6 получится тридцать
Умножение дает нам произведение . В 5 х 6 = 30 произведение равно 30.
÷ ИЛИ /
знак деления
Знак деления представляет:
подразделение
15 ÷ 3 = 5 15 / 3 = 5 пятнадцать разделить на три равно пяти пять получится пятнадцать трижды если пятнадцать разделить на три получится пять если три разделить на пятнадцать получится пять
Деление
дает нам частное . В 15 ÷ 3 = 5 частное равно пяти.
Подытожим вышеописанные четыре операции следующим образом:
| операция | результат | ||
|---|---|---|---|
| дополнение | «плюс» | 2 + 2 = 4 | сумма |
| вычитание | «минус» | 5 — 3 = 2 | разница |
| умножение | «раз» | 3 х 5 = 15 | товар |
| отделение | «делится на» | 21/7 = 3 | частное |
=
знак равенства
Знак равенства представляет равенство :
3 + 4 = 7 три плюс четыре равно семь
Обратите внимание, что мы обычно говорим, что равно НЕ равно:
- два плюс два равно четыре
-
два плюс два равно четырем
< меньше
3 < 4 три меньше четырех
больше
4 > 3 четыре больше трех
НЕ равно
x ≠ z x не равно z
больше или равно
x ≥ z x больше или равно z
меньше или равно
z ≤ x z меньше или равно x
дробь
см.
.
десятичный разделитель | точка
Десятичный разделитель отделяет целое число от его дробной части справа:
1,23
В английском языке десятичным разделителем обычно является точка (.)
Обратите внимание, что в некоторых языках десятичным разделителем является запятая (,)
см. десятичные дроби
,
разделитель тысяч
В английском языке разделитель тысяч разделяет целые числа на группы по три справа.
10 987 654 321
В английском языке разделителем тысяч обычно является запятая (,)
Обратите внимание, что в некоторых языках разделителем тысяч является точка (.), а иногда и пробел ( )
см. тыс.
%
знак процента
Знак процентов указывает число или отношение в виде доли от 100 ( процентов ).
40% сорок процентов Только сорок процентов людей проголосовали за нее. Какой процент проголосовал за нее? Сорок процентов.

√16 = 4 квадратный корень из шестнадцати равен четырем квадратный корень из шестнадцати равен четырем
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2.
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1. Переходим ко второму выражению в скобках 6−4. Здесь лишь одно действие – вычитание, выполняем его 6−4=2.
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2.
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.
Ответ:
5+(7−2·3)·(6−4):2=6.
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)).
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3). Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5. Подставив найденное значение, получаем 3+1+4·5. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24. Исходное значение, после подстановки этого значения, принимает вид 4+24, и остается лишь закончить выполнение действий: 4+24=28.
Ответ:
4+(3+1+4·(2+3))=28.
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1, то после этого исходное выражение примет вид (4+(4+1)−1)−1. Опять выполняем действие во внутренних скобках, так как 4+1=5, то приходим к следующему выражению (4+5−1)−1. Опять выполняем действия в скобках: 4+5−1=8, при этом приходим к разности 8−1, которая равна 7.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
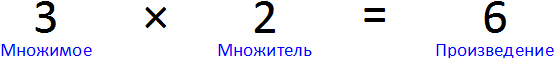
Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим например 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
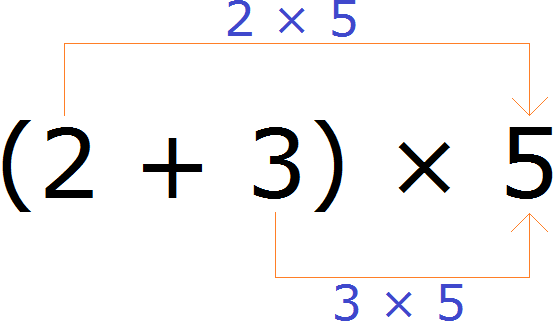
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!
Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.
Плюс как преимущество
Положительное число, которое после прибавления даёт сумму, также называется положительным слагаемым. Однако плюс может иметь и другое значение — преимущество.
В контексте математики, плюс как преимущество означает добавление чего-либо положительного или вычетание отрицательного. Например, если к определенной сумме добавляются дополнительные деньги или вычитается долг, то это плюс как преимущество.
Плюс в данном случае указывает на добавление или вычитание, что приводит к увеличению или уменьшению итогового значения. Использование операции сложения и вычитания позволяет получить разность двух чисел и определить, насколько они отличаются друг от друга.
Таким образом, плюс как преимущество позволяет вносить изменения в значение числа или переменной путем добавления или вычитания определенной величины, что приводит к изменению итогового результата.
Анализ сложной ситуации
Изучение изменений, которые происходят при сложении положительных и отрицательных чисел, помогает понять, что дает плюс на минус при сложении.
Когда мы складываем положительное число с отрицательным числом, то происходит вычитание или, иначе говоря, вычетание отрицательного числа из положительного. Результат такого сложения будет отрицательным числом.
Например, если мы сложим число 5 и -3, то получим сумму 2, которая будет отрицательным числом.
Если же мы складываем отрицательное число с положительным числом, то происходит добавление или прибавление отрицательного числа к положительному. Результат такого сложения будет положительным числом.
Например, если мы сложим число -4 и 2, то получим сумму -2, которая будет положительным числом.
Таким образом, сложение положительных и отрицательных чисел может привести как к получению положительного результата, так и к получению отрицательного результата, в зависимости от знаков складываемых чисел.
| Сложение | Результат |
|---|---|
| Положительное число + Отрицательное число | Отрицательное число |
| Отрицательное число + Положительное число | Положительное число |
Мотивация к развитию
Прибавление и сложение двух положительных чисел дает сумму, которая также будет положительной. Это положительное число может служить мотивацией для людей к развитию и достижению новых целей. Когда мы добавляем что-то положительное к уже имеющемуся, мы получаем еще больше положительности.
Однако, когда мы складываем положительное и отрицательное число, мы получаем разность, которая может быть как положительной, так и отрицательной. В таком случае, мотивация к развитию может возникнуть из стремления изменить отрицательную ситуацию и получить положительные результаты.
Вычетание и вычитание играют важную роль в мотивации к развитию. Когда мы отнимаем что-то от уже имеющегося, мы снижаем нашу запасенную энергию или ресурсы. Это может быть мотивацией для нас, чтобы вложить больше усилий и восстановить потерянное. Получение положительного результата после вычитания может быть сильной мотивацией для продолжения развития и достижения успеха.
Таким образом, добавление и вычитание чисел можно рассматривать не только в математическом смысле, но и в контексте мотивации к развитию. Взаимосвязь между положительными и отрицательными числами может помочь нам преодолевать трудности, стремиться к изменениям и достигать новых высот в нашей жизни.
История открытия закона умножения минус на минус
Происхождение понятия «число»
До развития математики и науки в целом люди пользовались только количественными выражениями, не прибегая к формулированию формул и алгебраических уравнений. Однако уже в древности было замечено, что определенные количества могут быть как положительными, так и отрицательными.
Сначала арифметические действия выполнялись только с положительными числами, но потребность в использовании отрицательных чисел возникла при записи температур, денежных сумм и некоторых других характеристик.
Открытие закона умножения минус на минус
Умножение является одним из наиболее базовых арифметических действий, а знание теоремы может быть полезным для решения многих задач. Математики долгое время боролись с проблемой умножения отрицательных чисел и только в 1202 году легендарный итальянский математик Леонардо Фибоначчи доказал, что минус умножить на минус дает плюс. Эта теорема стала важным шагом в математике. Многие для доказательства использовали аналогию с обычными числами. Например, посмотрев на таблицу, они замечали, что минус на минус не должно давать плюс, но только они забывали, что начинают с минусов, что и создавало путаницу.
Примеры применения закона умножения минус на минус
- Представим себе, что мы машинисты и везем поезд. Если мы отправляемся вперед, тогда на рельсах остается «плюс один», который понятно может означать массу нашего поезда. Если же мы движемся назад, то на рельсах остается «минус один». И если мы еще раз повернемся и пойдем назад, получается «-1» умноженное на «-1» и мы получаем плюс первый наших вагонов.
- Другим примером может быть произведение двух матриц. Здесь каждый элемент матрицы присваивает не только характеристику объекту, но и его знак.
ПЛЮС МИНУС
Плюс и минус — это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками.
При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число.
В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус. Если положительную дробь умножить или разделить на отрицательную дробь получится отрицательное число. Это число может быть целым или дробным. Произведение положительного числа на отрицательное — число отрицательное, частное положительного числа на отрицательное число — отрицательное число. Если числитель дроби положительный, а знаменатель отрицательный — дробь (или целое число) будет отрицательной.
При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный — дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное — число отрицательное, частное отрицательного числа на положительное число — отрицательное число.
Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.
ВОПРОС — ОТВЕТ
«Кто ввел знаки сложения и вычитания в математику?» — первое употребление слов plus (больше) и minus (меньше) как обозначения действия сложения было найдено историком математики Энестремом в итальянской алгебре четырнадцатого века. Вначале действия сложения и вычитания обозначали перввыми буквами слов «p» и «m». Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».
«Минус 6 делить на минус 3 как быть?» — сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс. Теперь прилепливаем полученный плюс к ранее полученной двойке
Впрочем, знак «+» перед числами писать не принято, поэтому красивее и правильнее будет так:
«Если число со знаком минус спереди умножаем на такое же число?» — решение смотри выше.






























