Содержание
-
Слайд 1
правила
по математике
для начальных классов -
Слайд 2
0 1 2 3 4 5 6 7 8 9
Это арабские цифры. Их всего десять.
I II III IV V VI VII VIII IX X …
Это римские цифры.
>больше +плюс -
Слайд 3
3 > 2
2 7
4 -
Слайд 4
Числа, которые делятся на 2, называютсяЧЁТНЫМИ:
2 4 6 8 10…
Числа, которые не делятся на 2, называются НЕЧЁТНЫМИ:
1 3 5 7 9 11…
При сложении чётных чисел получается чётное число, при сложении нечётных тоже получается чётное число:
4+2=6 3+5=8.
Если складывают нечётное число с чётным, то в ответе будет нечётное число:
5+2=7. -
Слайд 5
a + b = c
Прибавить 1 к какому-либо числу – значит назвать следующее за ним по порядку число
1 2 3 4 5 6 7 8 9 . . .
6 + 1 = 7 -
Слайд 6
От перестановки слагаемых сумма не изменяется
a + b = b + a
Если одно из слагаемых равно 0, то сумма равна другому слагаемому
a + 0 = a
0 + a = a -
Слайд 7
Вычесть 1 из какого-либо числа – значит назвать предыдущее число
1 2 3 4 5 6 7 8 9 . . .
7 – 1 = 6 -
Слайд 8
2 = 1 + 1
3 = 1 + 2 = 1 + 1 + 1
4 = 1 + 3 = 2 + 2
5 = 1 + 4 = 2 + 3
6 = 1 + 5 = 2 + 4 = 3 + 3
7 = 1 + 6 = 2 + 5 = 3 + 4
8 = 1 + 7 = 2 + 6 = 3 + 5 = 4 + 4
9 = 1 + 8 = 2 + 7 = 3 + 6 = 4 + 5 -
Слайд 9
Одно из слагаемых надо разложить так, чтобы одна из промежуточных сумм была равна 10.
7+5=7+(3+2)=(7+3)+2= 10+2=12
Таким же способом можно решать примеры на вычитание
15-7= 15-(5+2)=(15-5)-2=10-2=8 -
Слайд 10
Прибавить число к сумме, а также сумму к числу можно, складывая числа в любом порядке
(а + b) + c
(a + b) + c = a + (b + c)
(a + b) + c = (a + c) + b
a + (b + c)
a + (b + c) = (a + b) + c
a + (b + c) = (a + c) + b -
Слайд 11
Вычесть из суммы число можно несколькими способами (a + b) – c(a + b) – c = (a – c) + b(a + b) – c = (b – c) + aЕсли перед скобкой в выражении стоит знак минус, то при раскрытии скобок знаки меняются на противоположныеa – (b + c) = a – b – ca – (b – c) = a – b + c
-
Слайд 12
Сложение можно проверить вычитанием. Для этого надо из суммы вычесть одно слагаемое. Если в результате получится другое слагаемое, значит сложение выполнено верно
a + b = c
c – a = b
c – b = a -
Слайд 13
Вычитание можно проверить сложением. Для этого надо к разности прибавить вычитаемое. Если в результате получится уменьшаемое, значит вычитание выполнено верно
a – b = c
c + b = a -
Слайд 14
2 3 = 6
первый второй произведение
множитель множитель
a b = c
От перестановки множителей произведение не меняется
a b = b a -
Слайд 15
Если один из множителей равен 0, то произведение равно 0.
a 0 = 0
0 a = 0
Если один из множителей равен 1, то произведение равно другому множителюа 1 = а
1 а = а -
Слайд 16
(a + b) c
(a + b) c = a c + b c
a (b + c)
a (b + c) = a b + a c -
Слайд 17
Если произведение двух чисел разделить на один из множителей, то получится другой множитель
a b = c
c : b = a
c : a = b -
Слайд 18
: 3 = 2
делимое делитель частное
a : b = c
Если делитель равен 1, то частное равно делимому
а : 1 = а
Если делимое равно делителю, то частное равно 1
а : а = 1
Если делимое равно 0, то частное равно 0
0 : а = 0
Делить на 0 нельзя! а : 0 -
Слайд 19
На 2 делятся числа, оканчивающиеся на чётную цифру:
28:2=14 174:2=87
На 3 делятся числа, сумма цифр которых делится на 3:
225:3=75 (2+2+5=9. Число 9 делится на 3)
На 4 делятся числа, если двузначное число, образованное двумя последними цифрами, делится на 4:
216:4=54 (две последние цифры делимого составляют число 16, которое делится на 4)
На 5 делятся числа, оканчивающиеся на 5 или 0:
70:5=14 145:5=29 -
Слайд 20
ДЕЛЕНИЕ ЧИСЛА НА ПРОИЗВЕДЕНИЕ
-
Слайд 21
Если делимое разделить на частное, получится делитель
а : b = c
Проверка: а : с = b
Если делитель умножить на частное, получится делимое
a : b = c
Проверка: с b = a -
Слайд 22
Если делимое не делится на делитель, например 7 : 3, то надо подобрать ближайшее число, меньше 7, которое делится на 3 без остатка
7:3(6+1):36:3+12 (остаток1)
Остаток всегда должен быть меньше деления. -
Слайд 23
Увеличить число на несколько единиц – значит прибавить
a + b
Увеличить число в несколько раз – значит умножить
a b
Уменьшить число на несколько единиц – значит вычесть
a – b
Уменьшить число в несколько раз – значит разделить
а : b -
Слайд 24
Х с = а с : Х = а
Х = а : с Х = с : а -
Слайд 25
Периметр– это сумма сторон геометрических фигур (квадрата, прямоугольника и т. д.), обозначается латинской буквой Р.
Единицыизмерения– миллиметры (мм), сантиметры (см), метры (м).
Периметр прямоугольника
Р = a+b+a+b = 2 a+2 b = 2 (a+b)
Периметр квадрата
Р = а+а+а+а = 4 а
Периметр треугольника
Р= a + b + c -
Слайд 26
ПЛОЩАДЬ ФИГУРЫ
Площадь– это внутренняя часть фигуры (прямоугольника, квадрата и т. д.), обозначается латинской буквойS.
Единицы измерения – квадратные километры (км²), квадратные метры (м²), квадратные сантиметры (см²).
Площадь прямоугольника
S= a b
Площадь квадрата
S = a a
Посмотреть все слайды
Деление чисел нацело
Деление чисел нацело – это операция, при которой находят количество целых частей, которыми можно разделить одно число на другое. Например, если мы делим число 12 на число 3, то получаем, что 12 можно разделить на 3 целых части.
Для того чтобы выполнить деление нацело, необходимо полностью разделить делимое число на делитель без остатка. Если при делении остаются остатки, то результат не будет целым.
В математике также используется понятие «остаток от деления». Остаток от деления – это число, которое остается после того, как делимое число разделено на делитель. Остаток может быть равен нулю, если число делится нацело. Если же остаток не равен нулю, то результат деления будет числом с остатком.
В третьем классе ученики учатся выполнять простые задачи на деление нацело и находить остатки от деления.
Работа с линейкой и учебной транспортирной

В третьем классе математики учащиеся начинают знакомство с инструментами, которые помогают измерять длину и углы. Одним из таких инструментов является линейка.
Учащиеся также знакомятся с учебной транспортироной (угольником). Они учатся измерять углы, используя транспортирную.
При работе с транспортироной учащиеся узнают, как измерять углы, как их обозначать и как использовать отметки на транспортироне для измерения углов.
Изучение линейки и учебной транспортировны помогает учащимся развивать навыки измерения, точности в работе и математического мышления, что полезно для дальнейшего изучения математики и общего развития.
Длина, вес, объем
Длина. В 3 классе ученики изучают измерение длины различными единицами измерения: миллиметры, сантиметры, дециметры, метры, километры. Они изучают как переводить и сравнивать длины, решают задачи на сложение и вычитание длинных чисел. Также учатся находить длину отрезка на координатной плоскости.
Вес. В третьем классе изучение массы идет через измерение массы предметов в граммах и килограммах. Учащиеся изучают отношение долей, домножение и деление массы на десятичные дроби и целые числа, решают задачи на сравнение масс, сложение и вычитание массы чисел и использование единиц измерения массы в жизни.
Объем. В 3 классе ученики изучают объем геометрических тел: параллелепипед, куб, призма, цилиндр. Также они изучают как находить объем из метода воды, решают задачи на вычисление объема тел, используя базовые формулы.
- Результатом будет то, что ученики получат основные понятия в измерении длины, массы и объема и узнают о том, как применять эти знания на практике в быту.
- Если в классе есть слабые учащиеся, для них может потребоваться дополнительная помощь и тренировка, чтобы овладеть этим материалом.
Учебная программа по математике для 3 класса | K5 Learning
Темы по математике в 3 классе
Основные математические темы, изучаемые в 3 классе, обычно следующие:
Числа и операции
- Сложение и вычитание в пределах 1000
- разрядное значение единиц, десятков и сотен
- округление чисел до ближайших 10 или 100
- отношение между сложением и вычитанием
- введение в умножение
- введение в раздел
- умножить и разделить в пределах 100
- дроби как части целого
Геометрия
- классификация форм по их свойствам
- разделение фигур на равные части
- площадь и периметр неправильной формы путем подсчета квадратов
- площадь и периметр прямоугольников
Измерение
- оценка и измерение массы
- длины измерения (в том числе в долях дюйма)
- оценка и измерение объемов жидкостей
- определение времени с точностью до минуты и проблемы со словами времени
- Графические изображения и гистограммы для представления данных в нескольких категориях
- Линейные графики
Вы также можете ознакомиться с основными математическими стандартами для 3-го класса.
Рабочие листы по математике для 3-го класса
Выберите из сотен бесплатных математических листов для 3-го класса, организованных по темам:
| Разрядное значение и округление | Дроби и десятичные дроби |
| Порядок работы | Измерение |
| Дополнение | Считать деньги |
| Вычитание | Время и календарь |
| Умножение | Геометрия |
| Отдел | Проблемы со словами |
| Римские цифры |
Рабочие тетради по математике для 3 класса
Наши рабочие тетради по математике для 3 класса перечислены ниже; полная информация доступна в нашем книжном магазине. Рабочие тетради доступны по отдельности или в составе нашего пакета по математике для 1–3 классов.
Все правила: Математика 3 класс
- Производитель: УЛА
- Код товара: 9789662846041
- Наличие: В наличии
26 грн
Кол-во
- Описание
- Характеристики
- Отзывов (0)
Издание “
| ISBN | 9789662846041 |
| Автор | Сикора Ю.О. |
| Возраст | 3 класс |
| Издательство | Ула |
| Кол-во страниц | 36 |
| Серия | Просто. Быстро. Наглядно |
| Тип | справочник |
| Формат, размер | 21×9,5 см. |
| Язык | украинский |
Написать отзыв
Ваше имя
Ваш отзыв
Примечание: HTML разметка не поддерживается! Используйте обычный текст.
Рейтинг
Плохо
Хорошо
Теги:
УЛА
Рекомендуемые товары
Издание “Все правила: Украинский язык 3 класс” охватывает базовый материал по украинскому языку для ..
26.00 грн
Издание “Все правила: Украинский язык 4 класс” охватывает базовый материал по украинскому языку для ..
26.00 грн
Издание “Все правила: Математика 1-2 классы” охватывает базовый материал по математике для учащихся .
26.00 грн
Деньги и их обмен
В третьем классе школьники изучают тему «Деньги и их обмен». В ходе изучения этой темы ребята учаться определять номиналы монет, учатся считать деньги и находить сдачу. Кроме того, дети узнают, как правильно обращаться с деньгами и совершать их обмен.
Одним из важных аспектов, которые изучают в этой теме, является понимание того, что деньги – это средство обмена, а не самоцель. Ребята учатся распознавать различные монеты и банкноты и определять их стоимость.
Школьники также учатся совершать обмен денег, используя различные валюты. Для этого они учитывают курс валюты и правила ее обмена. Также дети знакомятся с терминами «покупка» и «продажа», учатся понимать, что при каждом обмене денег есть покупатель и продавец.
В конце темы «Деньги и их обмен» ребята уже должны уметь выполнять задания, связанные с подсчетом денег, нахождением сдачи и правильным обменом денег. Кроме того, они умеют пользоваться терминами, связанными с обменом валют и понимают, что деньги – это не просто бумажки и монетки, а важный инструмент в нашей жизни.
Знакомство с измерениями: длина, площадь и объем

В третьем классе ученики начинают знакомиться с понятием измерений. Они учатся определять длину, площадь и объем различных объектов.
Длина — это мера расстояния между двумя точками. Ученики учатся измерять длину с помощью линейки или мерной ленты. Они узнают, что длина может быть выражена в сантиметрах, метрах, километрах и других единицах измерения.
Площадь — это мера площади поверхности объекта. Ученики учатся измерять площадь с помощью квадратной сетки или формулы. Они узнают, что площадь может быть выражена в квадратных сантиметрах, квадратных метрах и других единицах измерения.
Объем — это мера занимаемого пространства объекта. Ученики учатся измерять объем с помощью геометрических фигур или формулы. Они узнают, что объем может быть выражен в кубических сантиметрах, кубических метрах и других единицах измерения.
В процессе работы с измерениями ученики учатся сравнивать и оценивать длину, площадь и объем различных объектов. Они также изучают принципы перевода из одной единицы измерения в другую.
Понимание измерений помогает ученикам развивать навыки ориентирования в пространстве, а также абстрактное и логическое мышление. Они учатся применять знания о измерениях в повседневных ситуациях, например при покупках или строительстве.
Таблица умножения

Таблица умножения – это одна из первых математических концепций, которую начинают изучать в начальной школе. Правильное знание таблицы умножения является основой для дальнейшего обучения математике.
Поскольку таблица умножения включает в себя множество цифр, то знать ее можно только через тренировку. Нужно регулярно повторять таблицу умножения и практиковаться в ее использовании, чтобы запомнить все цифры и быстро находить нужные ответы.
Таблица умножения до 10
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Отличное знание таблицы умножения поможет ученикам решать задачи быстрее и точнее в более сложных математических концепциях, таких как деление, применение дробей и работа с процентами.
Основные принципы решения математических задач
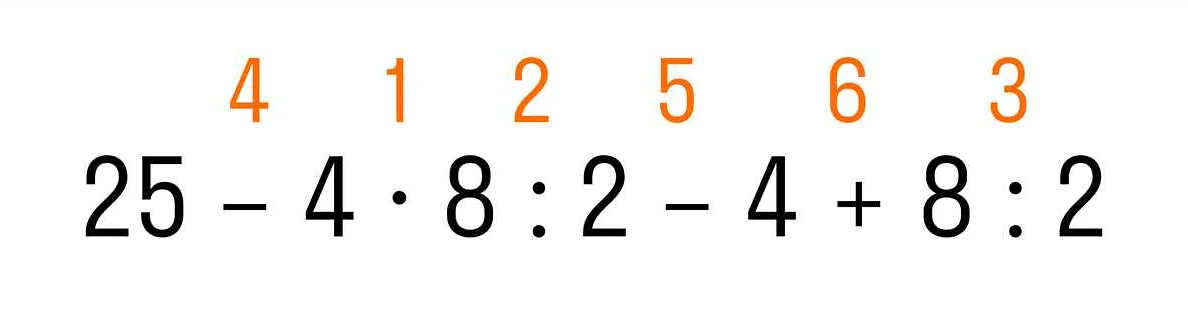
Решение математических задач в 3 классе основывается на нескольких основных принципах
Важно уметь правильно понимать условие задачи и анализировать его. Также необходимо знать основные математические понятия и операции, чтобы выполнять вычисления
Один из основных принципов решения задач — это разбиение задачи на более простые составляющие. Для этого нужно анализировать условие задачи и выделять в нем ключевые слова и фразы. Затем нужно определить, какие математические операции и понятия могут быть применены для решения задачи.
Другой важный принцип — это работа с числами и вычисления. В 3 классе дети уже должны знать основные арифметические операции: сложение, вычитание, умножение и деление. Для решения задач нужно уметь применять эти операции и выполнять вычисления, используя правильный порядок действий.
Также стоит обратить внимание на использование таблиц. Они могут быть полезны при решении задач, связанных с подсчетом и сравнением количества предметов
Таблицы помогут упорядочить информацию и сделать решение задачи более понятным и структурированным.
ОперацияПравила
| Сложение | Сложение чисел в любом порядке дает один и тот же результат. |
| Вычитание | Результат вычитания не зависит от порядка чисел. |
| Умножение | Порядок множителей не влияет на результат умножения. |
| Деление | Результат деления не зависит от порядка чисел. |
Следуя этим принципам и правилам, ребенок сможет успешно решать математические задачи и развивать свои навыки в области математики.
Все правила по математике для начальной школы
Электронная библиотека
- Просмотров: 54110
Говорят Дети
|
«Мам, принеси мне чай в комнату. Я и сама могла бы, но боюсь расплескать, а ты все-таки уже тридцать три года чашки носишь.» — Оля, 9 лет |
Новинки
- Речевые игры с лего
- Нейрологопедические прописи. Учимся читать и развиваем речь
- Стань буквой! Динамические паузы при обучении грамоте дошкольников и младших школьников
- 7 недорогих развивающих подарков детям
- Скорочтение для детей и не только
Прописи для детей
| Подготовка к школе | |
| Развитие моторики рук | |
| Обучение письму | |
| Интересные задания | |
| Современные методики |
Политика конфиденциальности
Числа и цифры
Математика начинается с изучения чисел и цифр. На уроках 3 класса дети знакомятся с числами от 0 до 999 и учатся записывать их в числовой форме и словесной форме.
Основными темами, касающимися чисел и цифр, являются:
- Чтение и запись чисел, состоящих из трех цифр;
- Сравнение чисел и нахождение наибольшего и наименьшего;
- Округление чисел до десятков и сотен;
- Определение четных и нечетных чисел;
- Разложение чисел на разряды и нахождение суммы цифр.
Работать с числами и цифрами помогают занимательные задачи и игры, которые не только развивают математические навыки, но и увлекают детей.
Знания о числах и цифрах пригодятся детям не только в математике, но и в повседневной жизни
Поэтому важно заниматься этой темой внимательно и добросовестно!































