Формула 4 класс

Часть 1

Упражнения

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

87

88

89

90

91

92

93

94

95

96

97

98

99

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

235

236

237

238

239

240

241

242

243

244

245

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

266

267

268

269

270

271

272

273

274

275

276

277

278

279

280

281

282

283

284

285

286

287

288

289

290

291

292

293

294

295

296

297

298

299

300

301

302

303

304

305

306

307

308

309

310

311

312

313

314

315

316

317

318

319

320

321

322

323

324

325

326

327

328

329

330

331

332

333

334

335

336

337

338

339

340

341

342

343

344

345

346

347

348

349

350

351

352

353

354

355

356

357

358

359

360

361

362

363

364

365

366

367

368

369

370

371

372

373

374

375

376

377

378

379

380

381

382

383

384

385

386

387

388

389

390

391

392

393

394

395

396

397

398

399

400

401

402

403

404

405

406

407

408

409

410

411

412

413

414

415

416

417

418

419

420

421

422

423

424

425

426

427

428

429

430

431

432

433

434

435

436

Задания внизу и на полях страницы

стр.5

стр.7

стр.8

стр.9

стр.10

стр.11

стр.12

стр.13

стр.14

стр.15

стр.17

стр.18

стр.19

стр.22

стр.23

стр.24

стр.25

стр.26

стр.27

стр.28

стр.29

стр.30

стр.34

стр.35

стр.36

стр.37

стр.38

стр.40

стр.42

стр.43

стр.44

стр.45

стр.46

стр.47

стр.48

стр.49

стр.50

стр.51

стр.52

стр.55

стр.56

стр.60

стр.61

стр.62

стр.63

стр.64

стр.65

стр.66

стр.67

стр.68

стр.69

стр.71

стр.72

стр.76

стр.77

стр.78

стр.79

стр.80

стр.81

стр.82

стр.83

стр.84

стр.85

стр.86

стр.87

стр.88

стр.89

стр.91

стр.94

Проверяем себя

1

2

3

4

5

6

7

8

9

10

Вариант 2

1

2

3

4

5

6

7

8

9

10

1

2

3

4

5

6

7

8

9

10

Вариант 2

1

2

3

4

5

6

7

8

9

10

Вариант 2

Что узнали чему научились

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

Как найти площадь квадрата

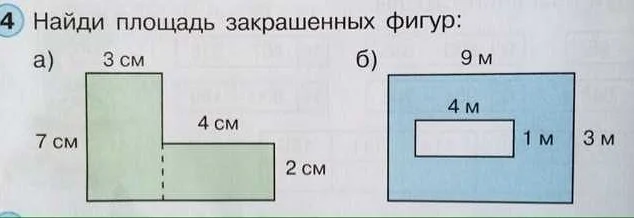
Квадрат — это геометрическая фигура, которая имеет четыре равные стороны и четыре прямых угла. Чтобы найти площадь квадрата, нужно знать длину одной его стороны.

Например, если длина стороны квадрата равна 5 сантиметров, то его площадь будет равна:

S = 5² = 25 сантиметров квадратных

Площадь квадрата всегда выражается в квадратных единицах, таких как сантиметры, метры или километры.

Вычисление площади квадрата может быть полезным не только для математики, но и для повседневной жизни. Например, если вам нужно купить квадратную плитку для пола, то для расчета количества необходимой плитки нужно знать площадь помещения и размерность плитки.

Основные математические формулы

Образование — то, что остается после того, как забыто все, чему учили в школе.

Игорь  Хмелинский, новосибирский учёный, ныне работающий в Португалии, доказывает, что без прямого запоминания текстов и формул развитие абстрактной памяти у детей затруднительно. Приведу выдержки из его статьи  «Уроки образовательных реформ в Европе и странах бывшего СССР»

Незнание таблицы умножения имеет и более серьезные последствия, чем неспособность обнаружить ошибки в расчетах на калькуляторе.

Наша долговременная память работает по принципу ассоциативной базы данных, то есть, одни элементы информации при запоминании оказываются связанными с другими на основе ассоциаций, установленных в момент знакомства с ними.

Далее, вновь поступающая информация попадет из кратковременной памяти в долговременную, если в течение короткого промежутка времени (несколько дней) мы столкнемся с нею многократно, и, желательно, в разных обстоятельствах (что способствует созданию полезных ассоциаций).

Однако при отсутствии в постоянной памяти знаний из арифметики, вновь поступающие элементы информации связываются с элементами, которые к арифметике никакого отношения не имеют – например, личностью преподавателя, погодой на улице и т.п.

Очевидно, такое запоминание никакой реальной пользы учащемуся не принесет – поскольку ассоциации уводят из данной предметной области, то никаких знаний, относящихся к арифметике, учащийся вспомнить не сможет, кроме смутных идей о том, что он вроде бы что-то когда-то об этом должен был слышать. Для таких учащихся роль недостающих ассоциаций обычно выполняют разного рода подсказки – списать у коллеги, воспользоваться наводящими вопросами в самой контрольной, формулами из списка формул, которым пользоваться разрешено, и т.п. В реальной жизни, без подсказок, такой человек оказывается совершенно беспомощным и неспособным применить имеющиеся у него в голове знания.

           Формирование математического аппарата, при котором формулы не заучиваются, происходит медленнее, нежели в противном случае. Почему? Во-первых, новые свойства, теоремы, взаимосвязи между математическими объектами почти всегда используют какие-то особенности ранее изученных формул и понятий.

Концентрировать внимание ученика на новом материале будет сложнее, если эти особенности не смогут извлекаться из памяти за короткий промежуток времени. Во-вторых, незнание формул наизусть препятствует поиску решения содержательных задач с большим количеством мелких операций, в которых требуется не только провести определенные преобразования, но и выявить последовательность этих ходов, анализируя применение нескольких формул на два-три шага вперед

Во-вторых, незнание формул наизусть препятствует поиску решения содержательных задач с большим количеством мелких операций, в которых требуется не только провести определенные преобразования, но и выявить последовательность этих ходов, анализируя применение нескольких формул на два-три шага вперед.

Практика показывает, что интеллектуальное и математическое развитие ребенка, формирование его базы знаний и навыков, происходит значительно быстрее, если большая часть используемой информации (свойства и формулы) находиться в голове. И чем прочнее и дольше она там удерживается, тем лучше.

НАДО ЛИ ВАС ДАЛЬШЕ УБЕЖДАТЬ В ТОМ, ЧТО ФОРМУЛЫ НАДО ЗНАТЬ НАИЗУСТЬ? 

Единицы измерения площади

Площадь — это величина, которая описывает, сколько плоских единиц (квадратных метров, квадратных сантиметров и т. д.) занимает поверхность. В математике используется множество единиц измерения площади, таких как квадратные метры, квадратные сантиметры, квадратные миллиметры, ара, гектар и т.д.

Квадратный метр (м²) — это основная международная единица измерения площади. Она равна площади квадрата со стороной, равной одному метру. Квадратные метры используются для измерения площади земельных участков, зданий и комнат.

Квадратный сантиметр (см²) — это единица измерения площади, которая равна площади квадрата со стороной, равной одному сантиметру. Она используется для измерения площади небольших поверхностей, например, листа бумаги или клетки на листке бумаги.

Ара — это мера площади, которая равна 100 квадратным метрам. Измерение в арах используется в сельском хозяйстве для определения площади полей, садов, угодий.

Гектар — это мера площади, которая равна 10 000 квадратным метрам. Гектар используется для измерения площади больших участков земли, например, ферм и лесных массивов.

• 1 квадратный метр = 10 000 квадратных сантиметров
• 1 квадратный метр = 1 000 000 квадратных миллиметров
• 1 гектар = 100 аров = 10 000 квадратных метров

Знание единиц измерения площади необходимо для решения многих задач в математике и повседневной жизни, таких как мероприятия по обустройству участков земли, строительство домов, покупка мебели и т.д.

Формула нахождения площади прямоугольника

Прямоугольник – это фигура, которая у каждого из своих углов имеет прямой угол. При этом противоположные стороны прямоугольника равны между собой.

Для того чтобы найти площадь прямоугольника, нужно умножить его длину на ширину.

Формула для нахождения площади прямоугольника выглядит так: S = a * b, где S – площадь, а и b – длина и ширина прямоугольника соответственно.

Например, если длина прямоугольника равна 5 см, а ширина – 3 см, то площадь будет равна: S = 5 * 3 = 15 (см2)

Найдя площадь прямоугольника, можно подобрать необходимое количество материала для его покрытия или рассчитать количество травы для укладки на газоне.

Некоторые математические обозначения и сокращения:

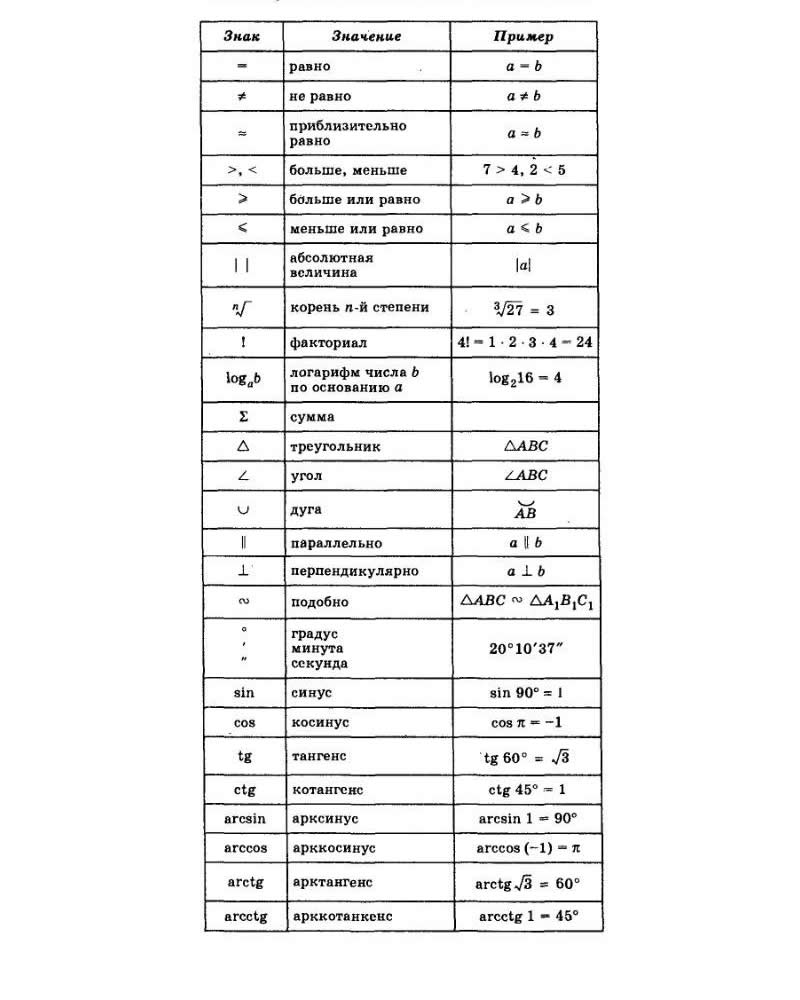
Число, делящееся на «2» без остатка называется чётным, не делящееся – нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, или ноль

Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»

Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и.т.д.)

Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»

Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т.е. числа, оканчивающиеся на «00», «25», «50», «75»

Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули

Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»

Абсолютная величина — формулы (модуль)

|a| ? 0, причём |a| = 0 только если a = 0;
|-a|=|a|
|a2|=|a|2=a2
|ab|=|a|*|b|
|a/b|=|a|/|b|, причём b ? 0;
|a+b|?|a|+|b|
|a-b|?|a|-|b|

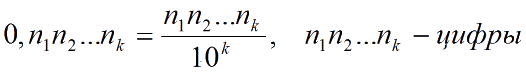
Пропорции

<span «>Два равных отношения образуют пропорцию:

Основное свойство пропорции

ad = bc

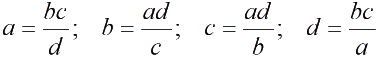
Пропорциипропорции

пропорцияпропорции

Средние величины

Двух величин:

n величин:

Среднее геометрическое
(среднее пропорциональное)

Двух величин:

n величин:

Двух величин:

n величин:

Двух величин:

n величин:

Квадратное уравнение

Определение. Уравнение вида ax2+bx+c=0, где a, b и c – любые действительные числа, причем а≠0, х – переменная, называется квадратным уравнением.

a – первый коэффициент, b – второй коэффициент, c – свободный член.

Решение неполных квадратных уравнений 

• ax2=0 – неполное квадратное уравнение (b=0, c=0). Решение: х=0. Ответ: 0.
• ax2+bx=0 – неполное квадратное уравнение (с=0). Решение: x (ax+b)=0 → x₁=0 или ax+b=0 → x₂=-b/a. Ответ: 0; -b/a.
• ax2+c=0 – неполное квадратное уравнение (b=0); Решение: ax2=-c → x2=-c/a.

Если (-c/a) , то действительных корней нет. Если (-с/а) > 0, то имеем два действительных корня:

Решение полных квадратных уравнений

 ax2+bx+c=0 – квадратное уравнение общего вида 

Дискриминант D=b2— 4ac.

Если D > 0, то имеем два действительных корня:

Если D=0, то имеем единственный корень (или два равных корня) х=-b/(2a).

Если D

 ax2+bx+c=0 – квадратное уравнение частного вида при четном втором

 коэффициенте b

 ax2+bx+c=0 – квадратное уравнение частного вида при условии: a-b+c=0. 

Первый корень всегда равен минус единице, а второй корень равен минус с, деленному на а:

x₁=-1, x₂=-c/a.

 ax2+bx+c=0 – квадратное уравнение частного вида при условии: a+b+c=0. 

Первый корень всегда равен единице, а второй корень равен с, деленному на а:

x₁=1, x₂=c/a.

Решение приведенных квадратных уравнений

x2+px+q=0 – приведенное квадратное уравнение (первый коэффициент равен единице).

Приведенные квадратные уравнения можно решать по тем же формулам, что и полные квадратные уравнения, однако, чаще для решения приведенных квадратных уравнений применяют теорему Виета.

Теорема Виета

Сумма корней приведенного квадратного уравнения x2+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

x₁+x₂=-p;  x₁∙x₂=q.

Теорема Виета для полного квадратного уравнения ax2+bx+c=0.

Сумма корней равна минус b, деленному на а, произведение корней равно с, деленному на а:

x₁+x₂=-b/a;  x₁∙x₂=c/a.

Формула нахождения площади треугольника

Площадь треугольника — это количество плоскости, заключенной между его тремя сторонами. Есть несколько способов найти площадь треугольника, но самый простой из них — использование формулы.

Формула нахождения площади треугольника имеет вид:

S = 0.5 × b × h

где b — длина основания, а h — высота, опущенная на основание.

Чтобы найти площадь треугольника, нужно измерить длину основания и высоту, опущенную на основание. Затем нужно подставить значения этих величин в формулу и выполнить необходимые вычисления.

Запомните формулу нахождения площади треугольника и применяйте ее в своих задачах. Она поможет вам быстро и точно найти площадь треугольника, не затрачивая много времени на решение задачи.

Тригонометрия

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Формулы приведения задаются в виде таблицы:

Как найти площадь круга

Круг — это геометрическая фигура, которую можно описать как множество точек на плоскости, равноудаленных от центра. Чтобы найти площадь круга, нам нужно знать его радиус.

Формула площади круга:

π x R²

где π — это число Пи (округленное до двух знаков после запятой, 3,14)

и R — радиус круга

Таким образом, чтобы вычислить площадь круга, нужно:

• Найти радиус круга
• Возвести радиус в квадрат
• Умножить полученный результат на число Пи

Если не знаете радиус круга, но знаете его диаметр (расстояние между двумя точками на круге, через центр), то радиус можно вычислить, разделив диаметр на 2.

Например, у круга диаметр 10 см, значит его радиус будет 5 см (10/2).

Подставляя значение радиуса в формулу, получим площадь круга:

π x 5² = 78,5 кв. см

Таким образом, мы нашли, что площадь круга с радиусом 5 см равна 78,5 квадратных сантиметров.

Шпаргалка по математике – Математика

1 см = 10 мм

1 дм = 10 см = 100 мм

1 м = 10 дм = 100 см

1 км = 1000 м

1 см = 100 мм

1 дм = 100 см = 10000 мм

1 м = 100 дм = 10000 см

1 км = 1000 000 м

1 км = 100 га = 10000 а

1 а = 100 м = 10000 дм

1 га = 100 а = 10000 м

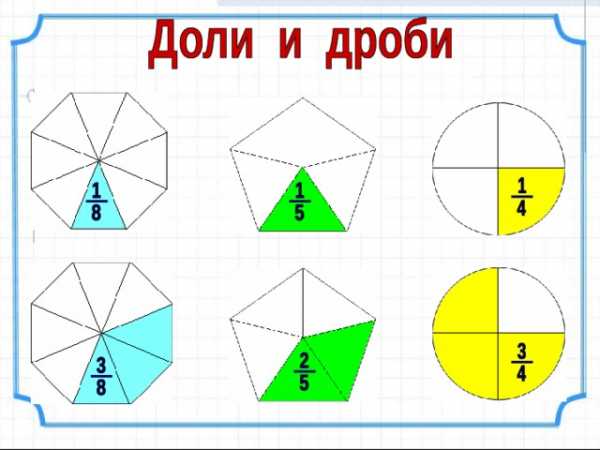
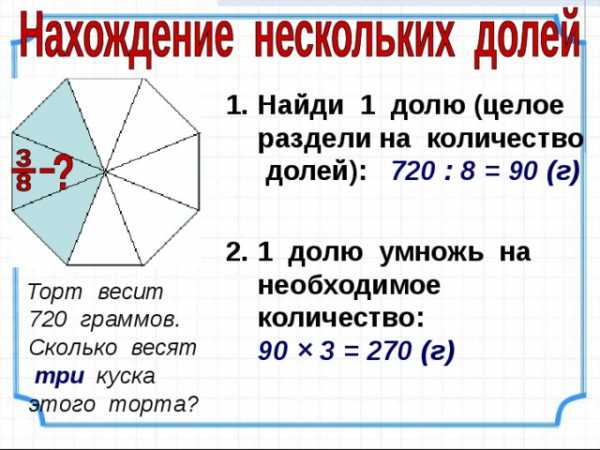
Торт весит 720 граммов. Сколько весят три куска этого торта?

Найди 1 долю (целое раздели на количество долей): 720 : 8 = 90 (г)

1 долю умножь на необходимое количество: 90 × 3 = 270 (г)

1 кг = 1000 г

1 ц = 100 кг

1 т = 10 ц = 1000 кг

1 мин = 60 с

1 ч = 60 мин

1 сут. = 24 ч

1 г. = 12 мес.

1 век = 100 лет

173490 17350

2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда.

3 58 741 2 58 741

6 4 3 74 7 3 74

173 4 90 173 5 00

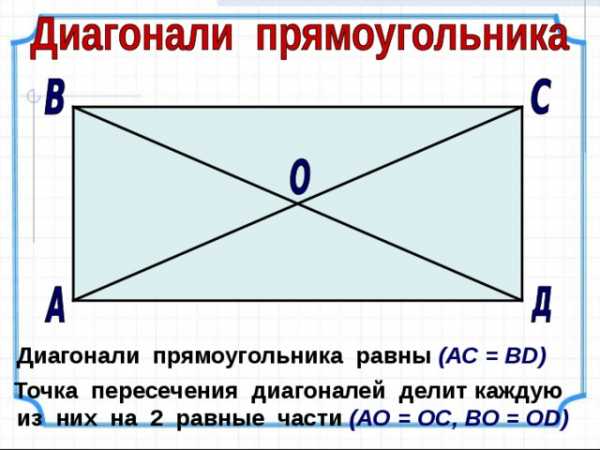
Диагонали прямоугольника равны (АС = В D )

Точка пересечения диагоналей делит каждую из них на 2 равные части (АО = ОС, ВО = О D )

– расстояние

– время

– скорость

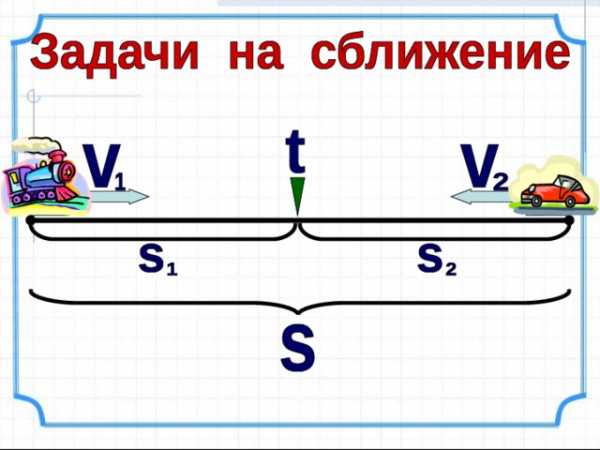
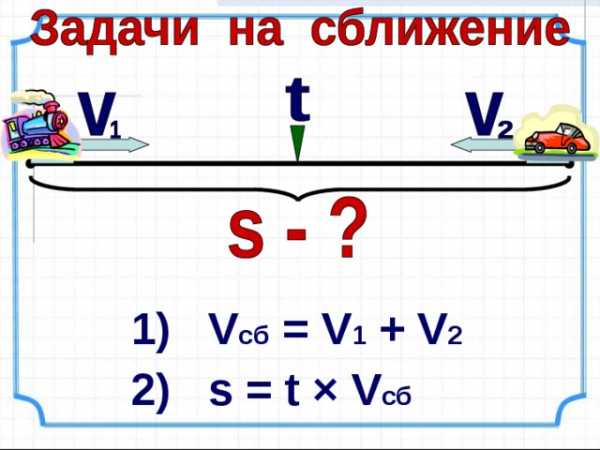
1) V c б = V 1 + V 2

2) s = t × V сб

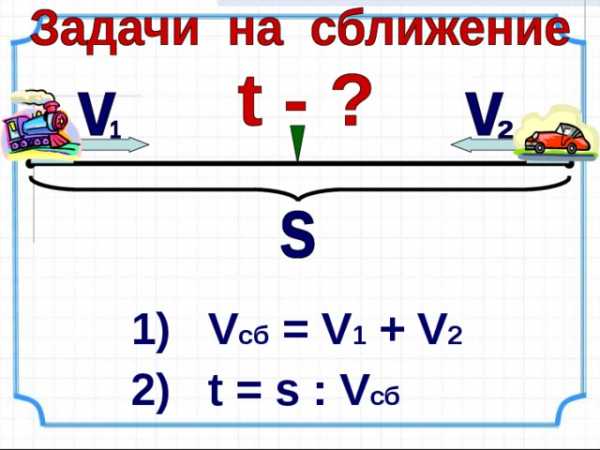
1) V c б = V 1 + V 2

2) t = s : V сб

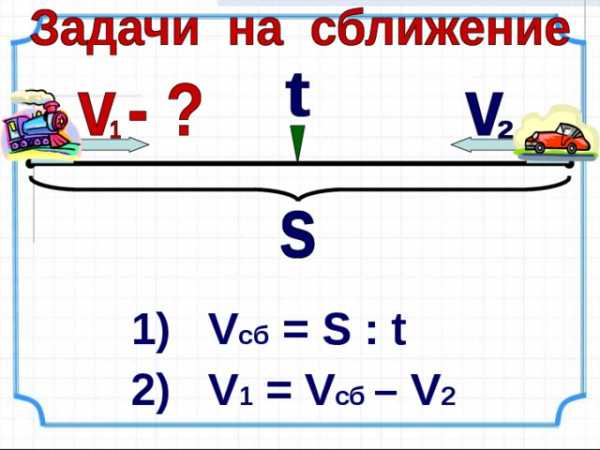
1) V c б = S : t

2) V 1 = V сб – V 2

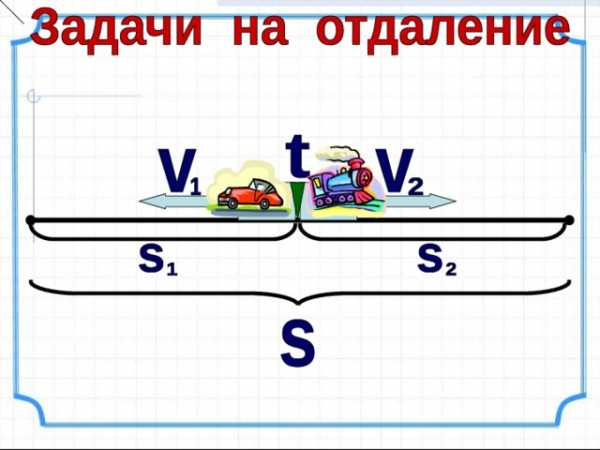
• Умножаем число на единицы, записывая результат так же, как при умножении на 1-зн. число.
• Умножаем число на десятки, начиная записывать результат под десятками.
• Складываем два неполных произведения, соблюдая порядок их записи

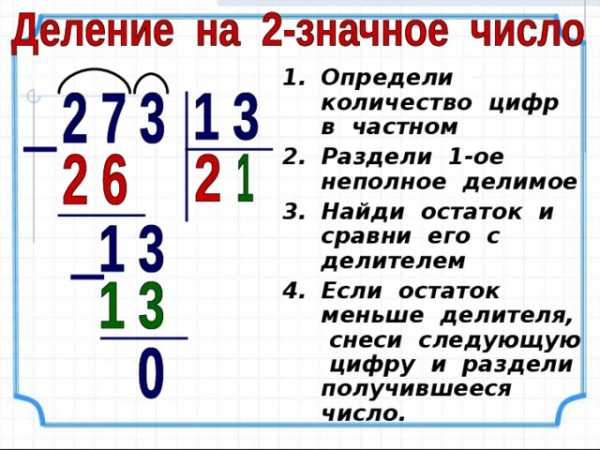
• Определи количество цифр в частном
• Раздели 1-ое неполное делимое
• Найди остаток и сравни его с делителем
• Если остаток меньше делителя, снеси следующую цифру и раздели получившееся число.

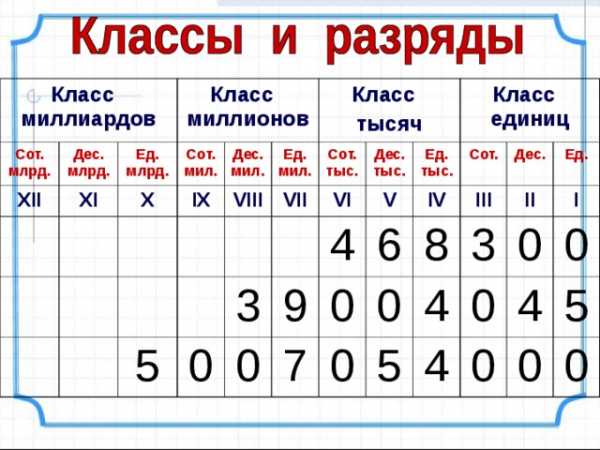
Класс миллиардов

Сот. млрд.

Дес. млрд.

XII

XI

Ед. млрд.

Класс миллионов

Сот.мил.

X

IX

Дес.мил.

Ед. мил.

VIII

тысяч

Сот. тыс.

VII

5

VI

3

Дес. тыс.

4

Класс единиц

Ед. тыс.

V

9

IV

7

Сот.

6

III

8

Дес.

5

3

4

II

Ед.

4

I

4

5

Все формулы по математике — Формулы под рукой

• ФОРМУЛЫ ПО АЛГЕБРЕ
• ФОРМУЛЫ ПО ГЕОМЕТРИИ
• ФОРМУЛЫ ПО ТРИГОНОМЕТРИИ

Обладатель премии Эйнштейна, известнейший британский исследователь в области теоретический физики Стивен Хокинг однажды рассказал, что получил должность профессора математики в Оксфордском университете, не имея специального образования.

На тот момент за его плечами были лишь изрядно подзабытые школьные знания по математике. Царицу наук постигал «на ходу», читая студенческий учебник с опережением программы на две недели.

Впоследствии студенты Хокинга вспоминали его занятия как исключительно познавательные и захватывающие!

Чтобы вспомнить (или освоить!) школьный материал было легче, предлагаем листать не страницы учебников и справочной литературы, а воспользоваться нашим сайтом, где удобная навигация и система поиска позволят быстро отыскать нужную формулу по предметам:

• арифметика;
• алгебра;
• геометрия;
• физика;
• химия.

От теории к практике

Бывает, что и материал знаком, да и формулы, теоремы и аксиомы по нужной теме — вот они, а задачка не поддается. Педагогический «диагноз»: нет опыта. Приобретается этот опыт при помощи решения типовых уравнений и задач. Предлагаем наиболее удачные и интуитивно понятные методики, которые уже помогли не одному ученику овладеть инструментарием точных наук!

Быстрее, выше, сильнее!

Возможно, сейчас ты и считаешь, что выучить все школьные формулы невозможно. Но на самом деле формул, необходимых для решения задач школьного уровня по математике, не более двухсот, а по физике — и того меньше! А это значит, что, заглядывая в наши справочники и освоив принципы решения типовых задач, можно постепенно запомнить все базовые формулы!

Какими бы сложными ни казались тебе задания твоих преподавателей сейчас, через какое-то время школьные, да и институтские стены могут показаться тебе тесными.

На нашем сайте собраны как часто используемые, так и гораздо более сложные формулы. Если захочешь знать больше, чем написано в школьном учебнике, начни с аксиомы — слов Марка Твена, который «никогда не позволял, чтобы школьные занятия мешали образованию!».

Геометрия на плоскости (планиметрия)

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Все математические формулы 1 по 4 класс :: trabursorre

Сочетательное свойство. Памятка «ФОРМУЛЫ». Скачать материал. Разработка урока Окружающий мир в 4 классе в стратегии РИСК.
Категории. Памятки по русскому языку . Памятки по математике . 2)чтобы найти время, надо расстояние разделить на скорость. t = S : V. Формула площади прямоугольника. S = а • b.
Формулы Арифметики: Законы действий над числами. Некоторые математические обозначения. Выбрать Учебник 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс. Разделы Центра.
V = S : t. 2)чтобы найти время, надо расстояние разделить на скорость. T = S : V Деление с остатком a=b*c+r, A-делимое b-делитель c-частное r-остаток Формула стоимости.
На этой странице собраны полезные шпаргалки по математике, алгебре и геометрии для учащихся 5-11 классов. Среди них часто используемые математические формулы, таблицы значений и многое другое.
Мария Петрова — Домашняя работа по математике за 2 класс к учебнику Л. Г. Содержит полный курс математических формул и справочных таблиц за школьный курс по математике, с 5 по 11 классы.
Формулы по математике для учащихся старших классов. Соотношение между натуральным и десятичным логарифмом: ln(N) = log(N) / log(e). Математические средние.
1-4 классы. Набор карточек. Ожидается. Аннотация к книге “Правила по математике в таблицах. Очень удобные с доступно изложенными правилами, формулами. Топ запросов по теме. четырехзначные математические таблицы синусы.
Прикладная математика Cправочник математических формул Примеры и задачи с решениями. Электронный справочник по математике: математические формулы по алгебре и геометрии, высшая математика, математика, математические формулы.
Математические формулы. Шпаргалка для ЕГЭ с математики -best. #математика. Свойства степеней.

Формула

Формула – это одно из важнейших понятий в математике. Основные формулы облегчают расчет и экономят время при решении уравнений. Поговорим о том, что такое формула, откуда они берутся и выделим основные формулы математики.

Формула – это всегда равенства. С левой стороны находится выражение, которое можно преобразовать, а с правой результат преобразования. Правильно использованная формула позволяет пропустить ряд действий, сохранив при этом правильный результат.

Формулу можно использовать в обе стороны. В геометрии это называют обратным действием, но чаще говорят просто: свернуть. Если выражение из левой части формулы превращается в правую, про него говорят, что свернули по формуле. Если наоборот: раскрыли скобки.

Посмотрим на примере. Воспользуемся формулой квадрата суммы: $(a+b)^2=a^2+2*ab+b^2$.

Имеется следующее выражение: $(2a+7b)^2=(2a)^2+2*(2a)*(7b)+(7b)^2=4a^2+28ab+49b^2$ – вот мы и раскрыли скобки по формуле квадрата суммы. Если нам потребуется конечное выражение превратить в начальное, то это будет уже обратное действие формулы.

Основными формулами математики считаются формулы быстрого умножения. Их не так много, поэтому лучше все заучить наизусть. Всего формул семь, каждая из них была выведена, для облегчения счета. Заучивают формулы в 4 этапа.

Первыми идут формулы суммы и разности квадратов. Формулу суммы мы уже знаем.

• $$(a+b)^2=a^2+2ab+b^2$$
• Квадрат разности не сильно отличается.
• $$(a-b)^2=a^2-2ab+b^2$$
• Знак минуса вполне логичен, и его достаточно просто запомнить.

Следующими запоминают куб суммы и куб разности. Они учатся быстрее, просто запоминаясь по аналогии.

$$(a+b)^3=a^3+3a^2*b+3a*b^2+b^3$$

$$(a-b)^3=a^3-3a^2*b+3a*b^2-b^3$$

Дальше идут формулы суммы и разности кубов, а так же разность квадратов. Разность квадратов записывается достаточно легко.

$a^2+b^2=(a+b)(a-b)$ – а вот формулы суммы квадратов нет. В начале курса 5 класса по математике ученики очень часто путаются формулы квадрата разности и разности квадратов. Попробуем научиться их различать.

Что такое разность квадратов? Это два числа в квадрате, из одного вычитается другое. А что такое квадрат разности? Из одного числа вычли другое, а результат возвели в квадрат. Достаточно один раз запомнить, а лучше понять, это объяснение и проблем с этими двумя формулами не будет никогда.

Следующими и последними идут формулы суммы и разности кубов. Они немного сложнее и для облегчения их запоминания придумали понятие неполного квадрата суммы и неполного квадрата разности.

Вспомним формулу квадрата суммы.
$$(a+b)^2=a^2+2ab+b^2$$
Обратим внимание на вторую часть.
$$a^2+2ab+b^2$$ – это и называется полным квадратом суммы. А неполным называется выражение:. $$a^2+ab+b^2$$

Это легко запомнить. По аналогии неполный квадрат разности: $a^2-ab+b^2$

$$a^2+ab+b^2$$. Это легко запомнить. По аналогии неполный квадрат разности: $a^2-ab+b^2$.

• Теперь приведем формулы суммы и разности кубов.
• $$a^3+b^3=(a+b)( a^2-ab+b^2)$$ – сумма кубов это произведение суммы чисел на неполный квадрат разности этих чисел.
• $$a^3+b^3=(a-b)( a^2+ab+b^2)$$ – разность кубов это произведение разности чисел на квадрат суммы этих чисел.

Как показывает практика, последние две формулы проще запомнить в словесной форме. К тому же эти формулы часто встречаются при решении простых уравнений. Поэтому, дабы не бежать каждый раз в интернет – проще их запомнить.

Мы дали определение понятию формулы, привели основные формулы математики и обозначили, что формулой можно пользоваться в обе стороны от знака равенства.

Средняя оценка: 4.6. Всего получено оценок: 145.

Вопрос-ответ:

Как найти площадь прямоугольника, если известны его стороны?

Для этого нужно умножить длину одной стороны на длину другой. То есть: S = a * b, где S — площадь, a и b — стороны прямоугольника.

Как найти площадь параллелограмма?

Площадь параллелограмма можно найти, умножив длину любой стороны на высоту, опущенную на эту сторону. То есть: S = a * h, где S — площадь, a — длина одной стороны, h — высота, опущенная на эту сторону.

Как найти площадь ромба?

Площадь ромба можно найти, умножив длину одной диагонали на длину другой диагонали и разделить полученное число на 2. То есть: S = (d1 * d2) / 2, где S — площадь, d1 и d2 — длины диагоналей.

Как найти площадь квадрата?

Площадь квадрата можно найти, умножив длину одной стороны на длину этой же стороны. То есть: S = a², где S — площадь, a — длина стороны квадрата.

Геометрия в пространстве (стереометрия)

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Часть 2

Упражнения

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

87

88

89

90

91

92

93

94

95

96

97

98

99

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

235

236

237

238

239

240

241

242

243

244

245

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

266

267

268

269

270

271

272

273

274

275

276

277

278

279

280

281

282

283

284

285

286

287

288

289

290

291

292

293

294

295

296

297

298

299

300

301

302

303

304

305

306

307

308

309

310

311

312

313

314

315

316

317

318

319

320

321

322

Страница 56

Задания внизу и на полях страницы

стр.4

стр.5

стр.6

стр.7

стр.12

стр.13

стр.14

стр.15

стр.16

стр.17

стр.20

стр.22

стр.23

стр.25

стр.26

стр.27

стр.28

стр.29

стр.30

стр.31

стр.32

стр.33

стр.34

стр.35

стр.36

стр.37

стр.42

стр.43

стр.44

стр.45

стр.46

стр.47

стр.48

стр.49

стр.50

стр.51

стр.54

стр.55

стр.56

стр.57

стр.58

стр.59

стр.60

стр.61

стр.62

стр.63

стр.64

стр.65

стр.66

стр.67

стр.70

стр.72

стр.73

стр.74

стр.75

стр.76

стр.77

стр.82

стр.83

стр.84

стр.86

стр.87

стр.89

стр.90

стр.91

стр.92

стр.95

стр.98

стр.99

стр.100

стр.101

стр.102

Странички для любознательных

Итоговое повторение

1

2

3

4

5

6

7

8

9

Что узнали чему научились

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

Символы вероятности и статистики

Символ	Название символа	Значение / определение	пример
P ( А )	функция вероятности	вероятность события A	P ( A ) = 0,5
P ( A ⋂ B )	вероятность пересечения событий	вероятность того, что событий A и B	P ( A ⋂ B ) = 0,5
P ( A ⋃ B )	вероятность объединения событий	вероятность того, что событий A или B	P ( A ⋃ B ) = 0,5
P ( A | B )	функция условной вероятности	вероятность события A данное событие B произошло	P ( A | B ) = 0,3
f ( x )	функция плотности вероятности (pdf)	P ( a ≤ x ≤ b ) = ∫ f ( x ) dx
F ( х )	кумулятивная функция распределения (cdf)	F ( х ) = Р ( Х ≤ х )
μ	Средняя численность населения	среднее значение совокупности	μ = 10
E ( X )	ожидаемое значение	ожидаемое значение случайной величины X	E ( X ) = 10
E ( X | Y )	условное ожидание	ожидаемое значение случайной величины X с учетом Y	E ( X | Y = 2 ) = 5
var ( X )	отклонение	дисперсия случайной величины X	var ( X ) = 4
σ 2	отклонение	дисперсия значений совокупности	σ 2 = 4
std ( X )	стандартное отклонение	стандартное отклонение случайной величины X	std ( X ) = 2
σ X	стандартное отклонение	значение стандартного отклонения случайной величины X	σ X = 2
	медиана	среднее значение случайной величины x
cov ( X , Y )	ковариация	ковариация случайных величин X и Y	cov ( X, Y ) = 4
корр ( X , Y )	корреляция	корреляция случайных величин X и Y	корр ( X, Y ) = 0,6
ρ X , Y	корреляция	корреляция случайных величин X и Y	ρ X , Y = 0,6
∑	суммирование	суммирование — сумма всех значений в диапазоне ряда
∑∑	двойное суммирование	двойное суммирование
Пн	Режим	значение, которое чаще всего встречается в популяции
MR	средний диапазон	MR = ( x макс + x мин ) / 2
Мкр	медиана выборки	половина населения ниже этого значения
Q 1	нижний / первый квартиль	25% населения ниже этого значения
2 квартал	медиана / второй квартиль	50% населения ниже этого значения = медиана выборки
3 квартал	верхний / третий квартиль	75% населения ниже этого значения
х	выборочное среднее	среднее / среднее арифметическое	х = (2 + 5 + 9) / 3 = 5,333
с 2	выборочная дисперсия	оценщик дисперсии выборки населения	s 2 = 4
с	стандартное отклонение выборки	Оценка стандартного отклонения выборки населения	s = 2
z x	стандартная оценка	z x = ( x — x ) / s x
X ~	распределение X	распределение случайной величины X	X ~ N (0,3)
N ( μ , σ 2 )	нормальное распределение	гауссово распределение	X ~ N (0,3)
U ( а , б )	равномерное распределение	равная вероятность в диапазоне a, b	Х ~ U (0,3)
ехр (λ)	экспоненциальное распределение	f ( x ) = λe — λx , x ≥0
гамма ( c , λ)	гамма-распределение	f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0
χ 2 ( к )	распределение хи-квадрат	f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2))
F ( k 1 , k 2 )	F распределение
Корзина ( n , p )	биномиальное распределение	f ( k ) = n C k p k (1 -p ) nk
Пуассон (λ)	распределение Пуассона	е ( К ) знак равно λ К е — λ / К !
Геом ( p )	геометрическое распределение	f ( k ) = p (1 -p ) k
HG ( N , K , n )	гипергеометрическое распределение
Берн ( p )	Распределение Бернулли

Признаки делимости на «2»

Число, делящееся на «2» без остатка называется чётным, не делящееся – нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, или ноль

Признаки делимости на «4»

Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»

Признаки делимости на «8»

Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и.т.д.)

Признаки делимости на «3» и на «9»

Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»

Признаки делимости на «25»

Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т.е. числа, оканчивающиеся на «00», «25», «50», «75»

Признаки делимости на «10», «100» и на «1 000»

Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули