Основной порядок выполнение действий для простых выражений
Для простых примеров, не имеющих скобок, существует единый порядок выполнения:
- вычисления выполняются слева направо;
- сначала делаем умножение и деление;
- затем выполняем сложение или вычитание.
Рассмотрим простейшие примеры математического порядка в выражениях с простыми вычислениями, которые легко можно сделать в уме, то есть без использования записи.
Пример 1
Поскольку в данном примере нет скобок, отсутствуют умножение и деление, поэтому выполнение действия производим по единому правилу.
Решение:
- из 7 вычитаем 3 (7 — 3 = 4);
- прибавляем 6 (4 + 6 = 10).
В итоге получается следующее выражение: 7 — 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10
Пример 2
Условие: необходимо вычислить выражение 6 : 2 ⋅ 8 : 3.
Порядок выполнения заключается в применении правил для примеров без скобок. Используется стандартный порядок вычисления, то есть слева направо.
Решение:
- делим 6 на 2 (6 : 2 = 3);
- умножаем результат на 8 (3 ⋅ 8 = 24);
- результат делим на 3 (24 : 3 = 8).
Получаем следующее: 6 : 2 ⋅ 8 : 3 = 3 ⋅ 8 : 3 = 24 : 3 = 8
Ответ: 6 : 2 ⋅ 8 : 3 = 8
Пример 3
Условие: необходимо вычислить, сколько будет 17 − 5 ⋅ 6 : 3 − 2 + 4 : 2.
В данном выражении присутствуют различные виды арифметических действий, включая умножение, деление, деление, вычитание.
Поэтому порядок в математике в данном примере будет следующий:
- выполняем деление и умножение в порядке слева направо;
- выполняем сложение и вычитание в обычном порядке.
Решение:
- 5 умножаем на 6 (5 ⋅ 6 = 30);
- делим 30 на 3 (30 : 3 =10);
- делим 4 на 2 (4 : 2 = 2);
- подставляем полученные цифры в исходное выражение (17 — 10 — 2 + 2 = 7).
В итоге расширенное решение данного примера выглядит следующим образом:
17 − 5 ⋅ 6 : 3 − 2 + 4 : 2 = 17 — 30 : 3 — 2 + 4 : 2 = 17 — 10 — 2 + 2 = 17 — 10 — 2 + 2 = 7 — 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 ⋅ 6 : 3 − 2 + 4 : 2 = 7
Если учеником порядок выполнения еще не усвоен, допускается использовать сверху цифры, полученные в результате промежуточных вычислений.
Математические действия с нулем
Круглый нуль такой хорошенький, Но не значит ничегошеньки.
В примерах нуль как число не встречается, но он может быть результатом какого-либо промежуточного действия, например:
5 × (8 : 2 – 4) = ?
- 8 : 2 = 4;
- 4 – 4 = 0;
- 5 × 0 = ?
При умножении на 0 правило гласит, что в результате всегда получится 0. Почему? Объяснить можно просто: что такое умножение? Это одно и то же число, сложенное с себе подобным несколько раз. Иначе:
0 × 5 = 0 + 0 + 0 + 0 + 0 = 0;
Деление на 0 бессмысленно, а деление нуля на любое число даст в результате всегда 0:
0 : 5 = 0.
Да и как может быть иначе, когда делить-то нечего? Если у вас нет яблок, поделиться с друзьями вам нечем.
Напомним другие арифметические действия с нулем:
а + 0 = а;
0 + а = а (от перестановки слагаемых сумма не меняется);
а – 0 = а;
0 – а = — а (число, противоположное вычитаемому).
Решение примеров
Для решения математических примеров нужно следовать определенному порядку действий. Этот порядок называется «Правило действий для решения примеров». Согласно этому правилу, умножение выполняется перед сложением.
При решении примеров нужно сначала выполнить все операции умножения, а затем сложения. Если в примере нет скобок, то вычислите умножение и сложение в порядке, указанном слева направо.
Например, рассмотрим следующий пример: 3 + 4 x 2.
Согласно «Правилу действий для решения примеров», сначала нужно выполнить умножение: 4 x 2 = 8. Затем выполняем сложение: 3 + 8 = 11.
Получается, что результатом этого примера будет число 11.
Таким образом, следуя правилу выполнения операций, мы можем решать примеры и получать верные результаты.
Дробная черта
Десятичная черта в выражении может быть заменена знаком деления, поэтому все, что выше и ниже десятичной черты, должно быть заключено в скобки. Например:.
| 13 + 2 | = (13 + 2) : (10 — 7). |
| 10 — 7 |
Знак деления в выражении может быть заменен десятичной чертой только в том случае, если не нарушена последовательность операций. Например, следующее выражение.
Замена выражения знаком разделения не допускается, поскольку такая замена нарушила бы последовательность выразительных действий.
| 20 : 4(2 + 3) ≠ | 20 | ; |
| 4(2 + 3) |
| 20 | = 20 : (4(2 + 3)). |
| 4(2 + 3) |
Вертикальная линия в выражении заменяет скобки, это означает, что выражения числителя и знаменателя должны быть вычислены отдельно, и первый результат должен быть разделен на второй результат.
Деление
Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.
Почему умножение первое?
Разберем математические действия на примере. Давайте собирать яблоки у бабушки на даче:
- Мама, папа и дедушка собрали по 50 яблок каждый и выполнили норму.
- Катя и Даша не ходили на уроки математики и помогали взрослым: собрали по 5 ядблок, норму не выполнили, съели 3 яблок, надкусили и испортили еще 6 яблок, 7 яблок было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все яблоки приностили бабушке, она укладывала их по кучкам.
Запишем результат «сбора» урожая в виде выражения:
- 50 + 50 + 50 – это кучки взрослых работников;
- 5 + 5 – это кучки девочек;
- 7 – изъято из карманов
- !!!! испорченное и надкусанное в зачет результата не идет.
Получаем пример для школы, запись учетчика результатов работы:
50 + 50 + 50 + 5 + 5 + 7 =?;
Здесь можно применить группировку: 3 кучки по 50 яблок − это можно записать через операцию умножения: 3 ∙ 50.
Две кучки по 5 – это тоже можно записать через умножение.
И одна кучка 7 яблок.
3 ∙ 50 + 2 ∙ 5 + 1 ∙ 7 =?
И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только яблоки. Нельзя сложить 50 яблок и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки – умножения. Совсем простыми словами – сначала выполняется умножение, а сложение уже потом. Если умножить 3кучки по 50 яблок каждая, то получится 150 яблок. А дальше их уже можно складывать с яблоками из других кучек.
250 + 10 + 7 = 267
При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.
Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.
Решение примеров с использованием действий со степенями

Чтобы решать примеры с использованием действий со степенями, необходимо понимать, что степень числа показывает, сколько раз нужно умножить это число само на себя.
Например, 2 в степени 3 равно 2 * 2 * 2 = 8. Это означает, что число 2 возведено в степень 3, то есть умножено само на себя три раза.
Если нужно перемножить числа, возведенные в степень, то необходимо умножить их обычным способом и получившееся число возвести в степень, равную сумме степеней этих чисел. Например, (2 в степени 3) * (2 в степени 2) = 2 * 2 * 2 * 2 = 16, что равно 2 в степени 5.
При делении чисел, возведенных в степень, нужно разделить числа обычным способом и возвести получившееся число в степень, равную разности степеней этих чисел. Например, (4 в степени 5) / (4 в степени 3) = 4 * 4 * 4 * 4 * 4 / 4 * 4 * 4 = 4 * 4 * 4 = 64, что равно 4 в степени 2.
Однако, если числа в степени свободно перемножать или свободно делить, то можно складывать или вычитать степени. Например, 2 в степени 3 * 2 в степени 2 может быть записано как 2 в степени (3 + 2) = 2 в степени 5.
Также стоит помнить, что возведение числа в отрицательную степень делает его обратным. Например, 2 в степени -2 равно 1 / (2 * 2) = 1 / 4.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок
:
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6
.
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7
отнимаем 3
, получаем 4
, после чего к полученной разности 4
прибавляем 6
, получаем 10
.
Кратко решение можно записать так: 7−3+6=4+6=10
.
Ответ:
7−3+6=10
.
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3
.
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6
делим на 2
, это частное умножаем на 8
, наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2
.
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5
умножаем на 6
, получаем 30
, это число делим на 3
, получаем 10
. Теперь 4
делим на 2
, получаем 2
. Подставляем в исходное выражение вместо 5·6:3
найденное значение 10
, а вместо 4:2
— значение 2
, имеем 17−5·6:3−2+4:2=17−10−2+2
.
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7
.
Ответ:
17−5·6:3−2+4:2=7
.
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Вы спрашивали: Что делать сначала плюс или минус?
Сначала умножение и деление, затем сложение и вычитание В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Почему сначала умножение а потом сложение?
Так всё же почему умножение выполняется первое, а только потом сложение? Ответ довольно прост. При умножении двух разных единиц измерения получается новая единица измерения, при сложении единицы измерения не меняются. При умножении мы получаем эту самую новую единицу измерения.
Что идет первым в скобках?
сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание; затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.
Как решить пример с двумя скобками?
Запомните правило:
- Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. …
- Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
Что значит выражение в математике?
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Как называются числа при умножении?
Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.
Какие действия в примере делаются первыми?
Сначала умножение и деление, затем сложение и вычитание В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Что сначала возведение в степень или умножение?
Для основных арифметических действий установлен следующий порядок: сначала выполняется возведение числа в степень, затем выполняется умножение и деление и в самую последнюю очередь выполняется сложение и вычитание.
Что такое арифметическое действие?
Сложение и вычитание, умножение и деление, возведение в степени и извлечение корня попарно являются обратными действиями. Правила первых четырех действий с целыми числами предполагаются известными.
Что такое двойные скобки?
Двойные скобки избегаются: нужно изменить предложение, чтобы двойных скобок не было, или использовать скобки разного рисунка. … Лопатина, круглые скобки используются для внешнего выделения, квадратные — для внутреннего, например: Виргинские острова, группа мелких о-вов в Вест-Индии.
Зачем нужны двойные скобки в математике?
Скобки для указания порядка выполнения действий Основное предназначение скобок – указание порядка выполняемых действий. Тогда выражение может иметь одну или несколько пар круглых скобок. По правилу всегда выполняется первым действие в скобках, после чего умножение и деление, а позже сложение и вычитание.
Как правильно решить уравнение со скобками?
В данном уравнении перед скобками стоят знаки минус и плюс. Чтобы раскрыть скобки в первом случае, где перед ними стоит знак минус, следует все знаки внутри скобок поменять на противоположные. Перед второй парой скобок стоит знак плюс, который на знаки в скобках никах не повлияет, значит их можно просто опустить.
Порядок действий в выражениях без скобок
Для правильного вычисления выражений, в которых нужно произвести более одного действия, нужно знать порядок выполнения арифметических действий. Арифметические действия в выражении без скобок условились выполнять в следующем порядке:
- Если в выражении присутствует возведение в степень, то сначала выполняется это действие в порядке следования, т. е. слева направо.
- Затем (при наличии в выражении) выполняются действия умножения и деления в порядке их следования.
- Последними (при наличии в выражении) выполняются действия сложения и вычитания в порядке их следования.
В качестве примера рассмотрим следующее выражение:
3 · 42 – 23 : 2 + 20
Сначала необходимо выполнить возведение в степень (число 4 возвести в квадрат и число 2 в куб):
3 · 16 – 8 : 2 + 20
Затем выполняются умножение и деление (3 умножить на 16 и 8 разделить на 2):
48 – 4 + 20
И в самом конце, выполняются вычитание и сложение (из 48 вычесть 4 и к результату прибавить 20):
48 – 4 + 20 = 44 + 20 = 64
Первый способ
- Каждое действие записывается отдельно со своим номером под примером.
- После выполнения последнего действия ответ обязательно записывается в исходный пример.
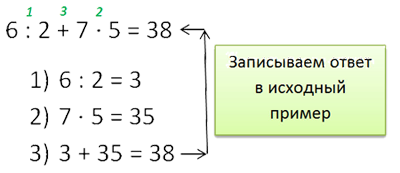
При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.
Второй способ
Второй способ называется запись “цепочкой”. Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.
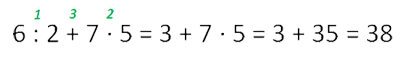
Если выражение содержит скобки, то сначала выполняют действия в скобках.
Внутри самих скобок действует правило порядка действий как в выражениях без скобок.
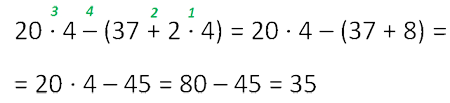
Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.
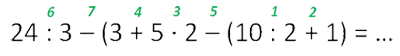

Как правильно решить пример
При вычислении примеров необходимо соблюдать порядок выполнения определенных операций. С помощью следующих правил вы поймете, в каком порядке выполняются действия и зачем нужны скобки.
- сначала выполняем слева направо все действия умножения и деления
- а потом слева направо все действия сложения и вычитания
Рассмотрим следующий пример последовательности действий.
Напомним, что математическая последовательность действий — слева направо (от начала примера к концу). При вычислении значения выражения его можно записать двумя способами.
Первый способ
- Каждое действие записывается отдельно со своим номером под примером.
- После выполнения последнего действия ответ обязательно записывается в исходный пример.
Если вы хотите вычислить результат действия в виде двух- и/или трехзначного числа, обязательно запишите вычисления в столбцах.
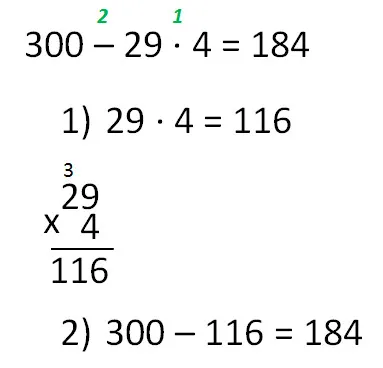
Второй способ
Второй метод известен как «цепное письмо». Все вычисления производятся в точно таком же порядке, но результат записывается сразу после знака равенства.
Операция сложения с положительными числами
Операция сложения с положительными числами осуществляется в математике для того, чтобы получить сумму двух или более положительных чисел.
Сложение выполняется с помощью знака «плюс» (+), который указывает на необходимость сложения чисел.
Операция сложения может быть использована для соединения или объединения двух или более значений. Например:
- Сумма двух положительных чисел всегда будет положительной: 3 + 2 = 5.
- Если число положительное, а второе слагаемое не указано, то результат сложения будет равен первому числу: 7 + хз = 7.
- Если число положительное, а второе слагаемое забыто или неизвестно, то нужно попросить кого-то подсказать: 4 + забыл = подскаите, плиз.
Также имеется простое правило, что сложение положительных чисел дает всегда положительный результат, даже если одно из слагаемых неизвестно или неопределено.
Таблица ниже демонстрирует результаты сложения положительных чисел:
| Первое слагаемое | Второе слагаемое | Результат сложения |
|---|---|---|
| 2 | 3 | 5 |
| 7 | хз | 7 |
| 4 | забыл | подскаите, плиз |
Плюс на плюс дает плюс
В математике, плюс на плюс может дать плюс, минус на плюс может дать минус, а плюс на минус варьируется от плюса до минуса или наоборот в зависимости от контекста и правил математики.
Операция сложения двух положительных чисел называется «плюс на плюс». Когда складываем два положительных числа, результатом будет положительное число, так как два положительных числа в сумме дают положительное число.
Например:
- 2 + 3 = 5
- 10 + 7 = 17
Операция вычитания положительного числа из положительного числа называется «минус на плюс». Когда вычитаем положительное число из положительного числа, результатом может быть как положительное число, так и отрицательное число, в зависимости от конкретных чисел.
Например:
- 5 — 2 = 3
- 10 — 7 = 3
Если одно число положительное, а другое — отрицательное, результат также может варьироваться.
Например, при операции «плюс на минус» и «минус на минус», результат будет:
- -2 + 3 = 1 (при «плюс на минус» результат будет положительным)
- -10 + 7 = -3 (при «плюс на минус» результат будет отрицательным)
- -5 — 2 = -7 (при «минус на минус» результат будет отрицательным)
- -10 — 7 = -17 (при «минус на минус» результат будет отрицательным)
Таким образом, плюс на плюс обычно дает плюс, но в зависимости от контекста операций и чисел, результат может быть разным. Решение конкретной математической задачи может помочь определить, какой будет результат операции плюс на плюс или других операций.
Правила работы с скобками
Скобки являются важным элементом в математике и используются для обозначения порядка выполнения операций. Они помогают определить, какие операции должны быть выполнены первыми. Вот основные правила работы с скобками:
- Правило 1: Скобки решаются внутри
Если внутри скобок находятся операции, то они должны быть выполнены первыми. Например, если есть выражение , то сначала нужно выполнить операцию внутри скобок, то есть сложить 2 и 3, а уже потом умножить результат на 4.
Правило 2: Скобки вписываются друг в друга
В математике можно использовать несколько видов скобок: круглые скобки , фигурные скобки и квадратные скобки . Если в выражении используются несколько видов скобок, то они должны быть вписаны друг в друга и быть правильно расставлены. Например, выражение корректно расставляет скобки по порядку и указывает, что сначала нужно выполнить операцию внутри круглых скобок, затем умножить результат на 4, а затем результат заключить в квадратные скобки и фигурные скобки.
Правило 3: Внешние скобки решаются последними
Если в выражении есть несколько уровней скобок, то сначала решаются внутренние скобки, а затем внешние. Например, если есть выражение , то сначала нужно выполнить операцию , а затем сложить результат с 2.
Правила работы с скобками помогают установить порядок выполнения операций в математическом выражении. Это позволяет избежать неоднозначности и получить правильный результат вычислений.
Решение примеров с использованием процентов
Решение примеров с процентами — это одна из базовых задач математики, которую необходимо уметь выполнять. Для начала, нужно уяснить, что процент — это доля числа, которая приводится к сотой доле (100%).
Чтобы решить пример с процентами, необходимо знать формулу: Часть (P) от целого (W) = Процент (x) / 100.
Например, если имеется число 80, а из него следует вычесть 20% процентов, необходимо выполнить следующие действия:
- Перевести процент в десятичную дробь: 20 / 100 = 0.2;
- Вычислить, какое число составляет 20% от 80: 80 * 0.2 = 16;
- Вычислить результат: 80 — 16 = 64.
Таким образом, из 80 следует отнять 16, что даст итоговый ответ равный 64.
Стоит заметить, что выполнение заданий с процентами сильно зависит от постановки задачи. Иногда требуется найти значение процента от заданного числа, в другой ситуации нужно вычислить процент от доли числа. Поэтому необходимо тщательно разбирать условие задачи и применять соответствующие формулы.
Зубодробительная задачка с очень простой математикой
Эта задача поставит в тупик половину интернета, но не вас.
Вот вам очень простой математический пример:
8 / 2(2 + 2)
Вы удивитесь, но большинство людей не смогут правильно это посчитать. Посчитайте сами и потом смотрите правильный ответ:
В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:
- То, что в скобках, выполняется в первую очередь. Если скобок несколько, они выполняются слева направо.
- При отсутствии скобок математические действия выполняются слева направо, сначала умножение и деление, потом — сложение и вычитание.
- Между множителем и скобкой (или двумя скобками) может опускаться знак умножения.
Разберём подробнее, что это значит в нашем случае.
1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:
8 / 2(2 + 2) → 8 / 2(4)
2. Между числом и скобкой можно опустить знак умножения. У нас перед скобкой двойка, то есть можно сделать такую замену:
3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.
Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:
8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16
Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.
А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами
Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:
«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!
 Та самая цитата.
Та самая цитата.
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки . П. С. Александров и А. Н. Колмогоров предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».
Если апеллировать к Фриде Максовне Шустеф, то выходит, что:
- В. Л. Гончаров говорит так: «Ребята, используйте черту и ставьте скобки, чтобы ни у кого не было вопросов про приоритет».
- Если у нас всё же битва арифметики и алгебры, то, по П. С. Александрову и А. Н. Колмогорову, пример нужно решать слева направо, как обычно. Они, конечно, предложили решать такое по-другому, но научное сообщество их не поддержало.
Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.
 Полная цитата из Шустеф, которая, оказывается, имеет в виду совсем не то.
Полная цитата из Шустеф, которая, оказывается, имеет в виду совсем не то.
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2.
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1. Переходим ко второму выражению в скобках 6−4. Здесь лишь одно действие – вычитание, выполняем его 6−4=2.
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2.
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.
Ответ:
5+(7−2·3)·(6−4):2=6.
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)).
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3). Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5. Подставив найденное значение, получаем 3+1+4·5. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24. Исходное значение, после подстановки этого значения, принимает вид 4+24, и остается лишь закончить выполнение действий: 4+24=28.
Ответ:
4+(3+1+4·(2+3))=28.
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1, то после этого исходное выражение примет вид (4+(4+1)−1)−1. Опять выполняем действие во внутренних скобках, так как 4+1=5, то приходим к следующему выражению (4+5−1)−1. Опять выполняем действия в скобках: 4+5−1=8, при этом приходим к разности 8−1, которая равна 7.
Сложение и вычитание
Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.
Самое простое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.
Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.
![]()
Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно 7. Посчитать можно на счетных палочках, камнях, яблоках– результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.
Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.
Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.
Использование таблицы приоритетов для сложных выражений
При работе с математическими выражениями, особенно со сложными, очень важно соблюдать правильный порядок выполнения операций. Для этого часто используется таблица приоритетов операций
Таблица приоритетов операций определяет порядок выполнения математических операций и помогает избежать ошибок при вычислении сложных выражений.
Вот основные правила, учитываемые при использовании таблицы приоритетов операций:
- Приоритет выполения операций определяется иерархией операций: умножение и деление имеют более высокий приоритет, чем сложение и вычитание.
- Операции с одинаковым приоритетом выполняются слева направо.
- Внутри выражений можно использовать скобки для указания порядка выполнения операций.
Ниже приведена таблица приоритетов операций:
| Операция | Приоритет |
|---|---|
| Скобки | Наивысший |
| Унарный минус | Высокий |
| Умножение, деление | Средний |
| Сложение, вычитание | Низкий |
Пример использования таблицы приоритетов:
- Вычисляем выражение в скобках.
- Выполняем операции с унарным минусом (если есть).
- Выполняем операции умножения и деления.
- Выполняем операции сложения и вычитания.
Используя таблицу приоритетов операций, можно правильно вычислить сложные выражения и избежать ошибок в расчетах.






























