Сложение чисел с разными знаками

Правила умножения минусов и плюсов

При умножении двух чисел, знак произведения зависит от знаков множителей.

• Если оба множителя положительные, то произведение также будет положительным.
• Если оба множителя отрицательные, то произведение также будет положительным.
• Если один из множителей положительный, а другой отрицательный, то произведение будет отрицательным.

Например:

• 2 * 3 = 6 — оба множителя положительные, произведение положительное.
• -2 * -3 = 6 — оба множителя отрицательные, произведение положительное.
• -2 * 3 = -6 — один множитель отрицательный, произведение отрицательное.
• 2 * -3 = -6 — один множитель отрицательный, произведение отрицательное.

Знание правил умножения минусов и плюсов поможет решать математические задачи с эффективностью и точностью.

ПЛЮС МИНУС

Плюс и минус — это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками.

При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число.

В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус. Если положительную дробь умножить или разделить на отрицательную дробь получится отрицательное число. Это число может быть целым или дробным. Произведение положительного числа на отрицательное — число отрицательное, частное положительного числа на отрицательное число — отрицательное число. Если числитель дроби положительный, а знаменатель отрицательный — дробь (или целое число) будет отрицательной.

При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный — дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное — число отрицательное, частное отрицательного числа на положительное число — отрицательное число.

Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.

ВОПРОС — ОТВЕТ

«Кто ввел знаки сложения и вычитания в математику?» — первое употребление слов plus (больше) и minus (меньше) как обозначения действия сложения было найдено историком математики Энестремом в итальянской алгебре четырнадцатого века. Вначале действия сложения и вычитания обозначали перввыми буквами слов «p» и «m». Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».

«Минус 6 делить на минус 3 как быть?» — сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс. Теперь прилепливаем полученный плюс к ранее полученной двойке

Впрочем, знак «+» перед числами писать не принято, поэтому красивее и правильнее будет так:

«Если число со знаком минус спереди умножаем на такое же число?» — решение смотри выше.

Правило «плюс на минус»

Правило «плюс на минус» часто вызывает путаницу и неоднозначность у людей, но на самом деле оно довольно простое и легко запоминается.

Суть правила заключается в следующем: когда перед числом стоит знак «плюс», а затем знак «минус», то можно удалить эти два знака и получить противоположное число.

Например:

• +(-5) = -5
• +(-10) = -10

Это правило особенно полезно при выполнении математических операций с числами. Например, если мы хотим прибавить к числу отрицательное число, то мы можем использовать правило «плюс на минус».

Например:

• 5 + (-3) = 5 — 3 = 2
• 10 + (-7) = 10 — 7 = 3

Также правило «плюс на минус» можно использовать для сокращения записи при выполнении сложных математических выражений.

Например:

• 2 + (-3) + (-4) + 6 = 2 — 3 — 4 + 6 = 1 — 4 + 6 = 3
• 10 + (-2) + (-5) + (-8) + 3 = 10 — 2 — 5 — 8 + 3 = 8 — 5 — 8 + 3 = 3

Таким образом, правило «плюс на минус» помогает нам легко работать с отрицательными числами и выполнять математические операции с минимальной путаницей и ошибками.

двойных отрицаний | Учебник по эффективному письму

Двойное отрицание — это выражение, содержащее два отрицательных слова.

Если в одном предложении используются два отрицания, может быть передано противоположное значение. Во многих британских, американских и других диалектах два или более отрицания могут использоваться с одним отрицательным значением.

Неверно:

Я никого не видел.

Однако английские и американские комментаторы употребления воспринимают двойную отрицательную форму как простоватую, необразованную и нестандартную. Вот более стандартная форма приведенного выше примера:

Правило для запоминания

Двойное отрицание — это утверждение, содержащее два отрицательных слова. Он не является частью стандартного английского языка, и его следует избегать.

Исправление двойных отрицаний

Правильно:

Я никого не видел.

Наиболее часто употребляемые отрицательные слова: нет, не, ничего, никогда, никто, никто, нигде, ни, и никто . Есть некоторые слова, которые имеют отрицательный элемент в своем значении, хотя они не содержат чрезмерно отрицательного аффикса. Эти слова: вряд ли, едва ли, едва, и т. д.

Неправильно:

Я еще не успел подумать об экзамене.

Правильно:

Я едва начал думать об экзамене.

Никто, ничего, никогда считаются эмфатичными. Будьте осторожны, когда используете эти слова. Используйте , а не кого-либо, никогда не используйте вместо этого .

Кто угодно, что угодно, и ever не являются отрицательными и должны использоваться с , а не с , чтобы передать отрицательное значение.

Допустимо использование двух отрицательных слов в предложении.

Правильно:

Я никак не могу навестить маму в этом году.

В приведенном выше предложении двойное отрицание используется эмфатически — «Я должен навестить свою мать».

Рассмотрим другой пример:

Правильно:

Я не был недоволен своей оценкой.

Здесь двойное отрицание используется для обозначения положительного или теплого значения — «Я не был недоволен, но и не был в восторге от своей оценки».

Две отрицательные идеи могут быть выражены союзами не… или и не. .. или . Когда 9За 0042 не следуют два или более глаголов, существительных или прилагательных, к ним присоединяются или .

Правильно:

Он не пьет и не танцует.

Используйте или после фразы, чтобы отделить и подчеркнуть второй глагол, прилагательное или существительное.

Правильно:

Наша главная цель не нефть и не электроэнергия. Это стабильность в регионе.

Мисс имеет отрицательное значение и не требует добавления отрицательного.

Неверно:

Я скучаю по тому, что не вижу его каждый день.

Правильно:

Я скучаю по нему каждый день.

Есть несколько способов исправления двойного отрицания:

Неверно:

Официантка только и делала, что курила.

Правильно:

Официантка только и делала, что курила.

Правильно:

Официантка ничего не делала, только курила.

Неправильно:

К концу дня у покупателя не осталось сил.

Правильно:

К концу дня у покупателя не осталось сил.

Правильно:

К концу дня у покупателя не осталось сил.

Пройди тест

Предыдущий

Раздел 3: Правила вычитания

При выполнении операции вычитания нужно знать, сколько будет плюс на минус. Это означает, что из большего числа необходимо вычесть меньшее число, чтобы получить результат. Правила вычитания включают следующие шаги:

1. Поставьте уменьшаемое (большее число) сверху.
2. Под ним поставьте вычитаемое (меньшее число).
3. Вычитание начинается с крайней правой цифры числа. Если цифра уменьшаемого больше цифры вычитаемого, то результат записывается прямо под ней.
4. Если цифра уменьшаемого меньше цифры вычитаемого, то вместо этой цифры ставится 10.
5. Единицу занимают из следующего старшего разряда, и от его цифры также вычитается 1.
6. Процесс повторяется, пока все цифры не будут вычтены или пока не будет достигнут крайний левый разряд числа.

Правильное применение правил вычитания позволяет получить точный результат и избежать ошибок при выполнении вычислений.

Уменьшаемое (большее число)	Вычитаемое (меньшее число)	Результат
57	28	29
94	61	33
187	95	92

Вычитание положительных чисел

Для выполнения вычитания положительных чисел нужно поставить одно число на место «на» и перед этим числом поставить знак «минус». Затем это число нужно сложить с другим положительным числом, и результатом будет число, которое будет «плюс» или «меньше» исходного числа.

Например, если мы вычитаем число 5 из числа 10, то запись будет выглядеть следующим образом: 10 — 5 = 5. В данном случае 5 будет «плюс», так как результат вычитания положительных чисел всегда будет положительным числом.

Вычитание положительных чисел может быть использовано во многих сферах. Например, оно может быть использовано для вычисления разности между двумя точками на числовой оси или для определения изменения значений в течение определенного периода времени.

Вычитаемое	Уменьшаемое	Разность
5	10	5
7	3	4
15	9	6

Таким образом, вычитание положительных чисел является важной математической операцией, которая позволяет определить разность между двумя положительными числами и использовать эту информацию в различных контекстах

Вычитание отрицательных чисел

Например, если отрицательное число -5 вычесть из отрицательного числа -3, то мы можем представить это как -3 + 5. Получается, что минус у -5 меняется на плюс, и мы складываем -3 с 5. В итоге получаем число 2.

Таким образом, при вычитании отрицательных чисел сначала меняем знак отрицательного числа на плюс, а затем складываем числа как обычно.

Вычитание чисел разных знаков

Для выполнения вычитания чисел разных знаков нужно следовать нескольким простым правилам:

1. Если число с положительным знаком вычитается из числа с отрицательным знаком, то результат будет иметь отрицательный знак.
2. Если число с отрицательным знаком вычитается из числа с положительным знаком, то результат будет иметь положительный знак.
3. Абсолютное значение результата будет равно разности абсолютных значений вычитаемого и уменьшаемого чисел.

Например, сколько будет 5 минус (-3)?

• Первый шаг: меняем знак второго числа. 5 — (-3) = 5 + 3 = 8.
• Ответ: 5 минус (-3) равно 8.

Вычитание чисел разных знаков важно уметь выполнять правильно, так как оно часто используется в реальных ситуациях и в математических задачах

Сложение чисел с разными знаками

Рассмотрим ситуацию.

Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?

Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.

Используем рассмотренный алгоритм при выполнении действий.

Суммируем-3 и 10. Для этого:

• определяем модули: -3=|3|, 10=|10|;
• сравниваем модули, определяя больший: |3|<|10|;
• от большего отнимаем меньший: 10 – 3=7;
• так как по условию 10 – число положительное, то и результат будет числом положительным.

Записывается в таком виде:

-3+10=10 – 3=7.

Выходит, у мальчика стало 7 яблок.

Рассмотрим еще один пример сложения чисел с разными знаками.

Вычислите сумму -28 и 11.

Известные слагаемые имеют разные знаки, то есть -28 является значением отрицательным, а 11–положительным. Чтобы суммировать слагаемые, необходимо воспользоваться ранее рассмотренным алгоритмом. Вначале, определяем модули и сравниваем их.

-28=|28|;

11=|11|;

28>11.

Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:

-28+11=-(28-11)=-17.

Учитывая рассмотренные примеры, можно сказать, что:

любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.

Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.

Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:

-150+50=-(150-50)=-100.

Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:

При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.

-150=|150|;

-100=|100|.

150>100;

-150<-100.

Действительно, при сложении с отрицательным числом уменьшаемое стало только меньше.

Какое действие первое плюс или минус

Приоритет арифметических операций является одним из основных понятий в математике и программировании. Правильное определение порядка выполнения арифметических операций позволяет получить ожидаемый результат вычислений.

В математике и в большинстве программированных языков для определения приоритета операций существуют установленные правила, которые позволяют определить, какое действие выполняется первым: сложение или вычитание.

Приоритет операций может быть описан следующими правилами:

1. Выполняются операции, заключенные в скобки;
2. Выполняются операции умножения и деления;
3. Выполняются операции сложения и вычитания в порядке их появления слева направо.

Таким образом, если в выражении присутствуют операции сложения и вычитания, они выполняются в порядке, в котором они следуют в выражении, начиная с самой левой операции и двигаясь по выражению вправо.

Например, в выражении «5 + 2 — 3» сложение «5 + 2» выполняется первым, а затем результат вычитается из числа 3. Таким образом, результатом этого выражения будет 4.

Если нужно изменить порядок выполнения арифметических операций, можно использовать скобки. Операции, заключенные в скобки, выполняются в первую очередь, а затем уже остальные операции в соответствии с правилами приоритета. Например, в выражении «(5 + 2) — 3» сначала выполняется операция в скобках, то есть сложение «5 + 2», и уже затем вычитание из числа 3. Таким образом, результатом этого выражения будет 4, как и в предыдущем примере.

Правильное определение приоритета арифметических операций позволяет получить верный результат вычислений и избежать путаницы при выполнении сложных выражений. При работе с программами и математическими выражениями всегда следует учитывать и применять правила приоритета операций.

Подтверждение правила

Для подтверждения правила, что при сложении минуса и минуса получается плюс, достаточно рассмотреть примеры из различных областей математики и физики.

1. Алгебра:
   • (-3) + (-2) = -5
   • (-7) + (-4) = -11
   • (-1) + (-1) = -2
2. Арифметика:
   • (-20) + (-10) = -30
   • (-50) + (-50) = -100
3. Физика:
   • Ускорение тела в одном направлении: -5 м/с²
   • Сила, действующая противоположно движению: -10 Н
   • Температурный градус, отнесенный к абсолютному нулю: -273 °C

Во всех перечисленных примерах сумма минусов является отрицательным числом, что подтверждает правило о сложении минуса и минуса, которое в итоге даёт положительный результат.

Произведение целых чисел с разными знаками.

Не важен порядок множителей положительное число умножаем на отрицательное или отрицательное число умножаем на положительное, в результате всегда будет отрицательное целое число.

Правило умножения двух целых чисел с разными знаками:При умножении двух целых чисел с разными знаками, их произведение будет равно целому отрицательному числу.

Если упростить определение то, обычно говорят:
“Минус на плюс дает минус”.
“Плюс на минус дает минус”.

Разберем пример:
Вычислить произведение целых чисел.
-4∙6=-24

А теперь докажем правильность этого решения.
-4+(-4)+(-4)+(-4)+(-4)+(-4)=-4∙6=-24
Шесть раз сложили число (-4).

Такой же ответ будет, если поменять местами числа.
6∙(-4)=-24

Пример:
-34∙2=-68

Как определить основное значениe знака плюс?

Когда знак плюс используется перед числом, он обозначает положительное число. Например, число «+5» означает «плюс пять» или «пять». Основное значение знака плюс в этом случае — это обозначение положительности числа.

Также знак плюс может использоваться в выражении или уравнении для обозначения операции сложения между числами или переменными. В этом случае основное значение знака плюс — это объединение двух или более чисел в одну сумму.

Примеры:

1. Основное значение знака плюс в выражении «2 + 3» — сложение чисел 2 и 3, что дает результат 5.

2. Основное значение знака плюс в числе «+7» — положительное число с величиной 7.

3. Основное значение знака плюс в уравнении «x + y = 10» — сложение переменных x и y со значением 10.

Вычитание отрицательных чисел и чисел с разными знаками

Мы уже знаем, как выполнять сложение и вычитание положительных и отрицательных чисел, но хочется сказать, что именно в этом разделе математики, большую роль играют противоположные числа. Для тех, кто забыл, напоминаем, какие числовые значения называются противоположными:

Если два числа отличаются только знаком, то они являются противоположными:-13 и 13, 141 и -141, 1000 и -1000.

Чтобы понять, какие правила необходимо соблюдать при выполнении вычитания чисел с разными знаками, давайте разберем задание.

Определите, чему будет равно значение выражения: от -510 отнять +210.

На первый взгляд задание очень простое и не вызывает никаких проблем. Но стоит записать разность в виде выражения:

-510-(+210)

Сразу возникает вопрос «Как вычитать, если уменьшаемое со знаком «минус», а вычитаемое со знаком «плюс»?».Чтобы решение подобных выражений не вызывало у вас трудностей, возьмите на заметку правило:

Чтобы выполнить вычитание чисел с разными знаками, нужно уменьшаемое оставить без изменений и прибавить к нему число, противоположное вычитаемому.

Например: -5-(+2).

Минус пять оставляем без изменений. Вычитаемое +2, а противоположное ему -2. Складываем уменьшаемое(-5) и число противоположное вычитаемому(-2): -5+(-2).

По правилу сложения отрицательных чисел, складываем модули(5+2) и ставим знак «-»:

-5+(-2)=-(5+2)=-7

Учитывая данное правило, получается, что к уменьшаемому(-510) необходимо прибавить значение,противоположное вычитаемому(210), таким числом будет -210:

Запишем выражение:

-510-(+210)=-510+(-210). Чтобы вычислить полученное выражение нужно сложить отрицательные значения, согласно правилу сложения отрицательных чисел:

-510-(+210)=-510+(-210)=-(510+210)=-720.

Вычисления окончены.

Рассмотрим следующее задание.

Найдите значение выражения: -248+248.

Используем правило сложения значений с разными знаками.

-248=|248|;

248=|248|;

248 – 248=0.

Следовательно, при сложении противоположных числовых значений в результате всегда будет 0.

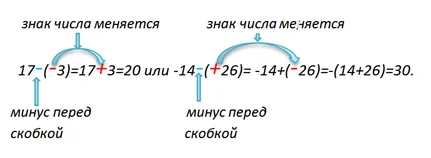
Зная правило вычитания отрицательных чисел, можем сделать вывод, что знаки, стоящие перед скобками, могут менять знак числа, находящегося в скобках.

К примеру, в выражении 19-(-4), при вычислении используем правило, согласно которого, к уменьшаемому прибавляем, число противоположное вычитаемому, то есть знак вычитаемого «-» меняем на противоположный «+». Получим:

Запомни! Если перед скобкой в математическом выражении стоит знак «минус», то знак числа в скобках меняется на противоположный.

Ну а сейчас, разберем задание, в котором перед скобкой стоит знак «плюс».

Вычисли: -36+(-7).

В этом задании воспользуемся правилом сложения отрицательных чисел– сложим модули числовых значений, а перед суммой поставим знак «минус»:

Мы видим, что «плюс» перед скобкой никак не повлиял на знак числа, стоящего в скобках. Запомни! Если перед скобками стоит «плюс», то знак числового значения, стоящего в скобках никак не меняется.

В выполнении рассматриваемых действий нет ничего сложного. Главное запомнить основные требования и придерживаться их в процессе любых вычислений! Если сразу запомнить все правила не получается, заходи на сайт 100уроков.ru и мы всегда с удовольствием напомним нужное правило или алгоритм.

Минутка истории

История математики утверждает, что человечество длительное время не принимало ряд отрицательных числовых значений. Данный вид чисел, казался непонятным и ненужным. Привычных нам знаков «плюс» и «минус» просто не существовало. Если возникала необходимость в записи отрицательно числа, то его записывали следующим образом «долг в 30 монет». И лишь математики Древней Индии и Китая, выполняли записи отрицательных чисел без употребления слова «долг», а просто использовали черные чернила, вместо синих.

Только в 3 веке греческий ученый Диофант, стал обозначать знак «минус» вот таким символом   .

Привычные нам знаки «+» и «-» появились в Германии в конце 15 века. Чешский ученый Ян Видман, отразил данные знаки в своей книге-пособии, помогающей подсчитывать прибыль и убытки чешским купцам. Стоит заметить, что данная книга была написана от руки и имела огромную популярность среди богатых людей того времени.

Раздел 4: Исключения

В предыдущих разделах мы рассматривали, сколько будет плюс на минус при расчете разных значений. Однако, существуют определенные исключения, которые также стоит учесть при проведении расчетов.

Вот некоторые из них:

• Разница между положительным и отрицательным числом может быть больше, чем указано. В этом случае результат будет соответствовать знаку числа с большим модулем.
• Если в выражении присутствует скобка, это может изменить результат вычислений. При вычислении выражения скобки имеют приоритет и выполняются в первую очередь.
• Если в выражении есть операторы с одинаковым приоритетом, они будут выполняться слева направо.
• При делении числа на ноль, получается ошибка, так как математическая операция деления на ноль не определена.

Важно учесть эти исключения при выполнении расчетов, чтобы получить точный и правильный результат

Сложение или вычитание с нулем

Примеры:

• 5 + 0 = 5
• 0 + 7 = 7
• -10 + 0 = -10

То же самое относится и к вычитанию с нулем. Как и при сложении, результатом будет оставшееся число без изменений.

Примеры:

• 8 — 0 = 8
• 0 — 4 = -4
• -3 — 0 = -3

Сложение и вычитание с нулем являются простыми операциями, которые можно использовать для проверки алгоритмов и математических задач.

Расчет с использованием скобок

При выполнении математических операций, включающих операторы плюс и минус, порядок выполнения выражений может существенно влиять на результат. Использование скобок позволяет управлять порядком операций.

Символы скобок используются для выделения групп операндов и операций и указывают, какие операции должны быть выполнены в первую очередь.

Например, выражение «5 + (3 * 2)» будет давать результат 11, так как сначала будет выполнено умножение, а затем сложение. В то же время выражение «5 + 3 * 2» будет давать результат 11, так как операции будут выполнены слева направо.

Использование скобок позволяет задать нужный порядок выполнения операций и получить точный результат расчетов в зависимости от поставленной задачи.

Комплексные расчеты

Комплексные расчеты представляют собой сложные математические операции, которые включают в себя как плюс, так и минус. Они позволяют определить сколько будет результат выражения в случае сочетания данных операций.

При выполнении комплексных расчетов необходимо учитывать порядок операций, так как он может влиять на итоговый результат. Расчеты выполняются по математическим правилам, где плюс увеличивает значение, а минус уменьшает его.

Для определения итогового значения выражения необходимо внимательно анализировать все плюсы и минусы в нем

С каждой операцией, результат может меняться, и поэтому важно правильно применять операции, чтобы получить точный и корректный ответ

Комплексные расчеты широко используются в различных сферах, таких как финансы, математика, физика и другие. Они позволяют проводить сложные вычисления и анализировать данные для принятия решений. Правильное выполнение комплексных расчетов является важным элементом в этих областях и может существенно влиять на полученные результаты.

Примеры решения примеров с минусом и плюсом

1. Сложение с разными знаками: Если нужно сложить два числа с разными знаками (одно положительное, другое отрицательное), то мы вычитаем из большего числа меньшее (без учета знака).

• Пример: -5 + 7 = 2 (7 — 5 = 2, знак остается от положительного числа)
• Пример: 15 + (-3) = 12 (15 — 3 = 12, знак остается от положительного числа)

2. Вычитание с разными знаками: Если нужно вычесть одно число с отрицательным знаком из другого числа с положительным знаком, то мы складываем эти числа (без учета знака).

• Пример: 8 — (-4) = 12 (8 + 4 = 12, знак остается от положительного числа)
• Пример: 21 — (-13) = 34 (21 + 13 = 34, знак остается от положительного числа)

3. Умножение с разными знаками: Если нужно умножить два числа с разными знаками (одно положительное, другое отрицательное), то результат всегда будет отрицательным числом.

• Пример: -6 * 3 = -18 (6 * 3 = 18, знак становится отрицательным)
• Пример: 7 * (-2) = -14 (7 * 2 = 14, знак становится отрицательным)

4. Деление с разными знаками: Если нужно разделить одно число с положительным знаком на другое число с отрицательным знаком (или наоборот), то результат всегда будет отрицательным числом.

• Пример: 21 / (-7) = -3 (21 / 7 = 3, знак становится отрицательным)
• Пример: (-10) / 2 = -5 (10 / 2 = 5, знак становится отрицательным)