Презентация на тему: "урок математики тема: «порядок действий.скобки» 2 класс лобова ольга викторовна моу сош с.васильевка.". скачать бесплатно и без регистрации

Примеры со скобками для 2 класса

Ознакомить учащихся с порядком действий в выражениях со скобками. Задания составлены профессиональными педагогами. Если производить действия в порядке их записи, четыре минус два плюс один, результат будет равен трём. Калининского р на Санкт Петербурга.примеры со скобками.31. ЯКласс — онлайн школа нового поколения. Теоретические уроки, тесты и задания по предмету Выражения со скобками, Порядок действий, 2 класс, Математика. Математика для 2 класса, для детей. Интересные рецензии пользователей на.

2 3 действия со скобками и без них. На конкретных примерах вы научитесь правильно производить вычисления таких выражений. Мои каналы: Математика 1 класс Математика 2 класс. Ознакомление с порядком выполнения арифметических действий в выражениях со скобками, содержащими сложение и вычитание. Развитие внимания, мышления, смекалки, математической речи. Воспитание о. С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки. Задачи для 3.

Задачи2 класс, выражения и примеры со скобками. Примеры с решениями по математике для 3 класса разной степени сложности. Каждое действие записывается отдельно со своим номером под примером. Каждая работа рассчитана на недельную нагрузку. Шимчук Наталья Петровна. Задания для повторения и закрепления.2 класс. В пособии представлены разнообразные задания по математике за курс 2 класса. Если выражение содержит скобки. ГДЗ, решебникМатематика 2 класс Богданович. Задание 202. Тренажер по математике. Цель урока:.

И деление с числами 2 и 3 из таблицы умножения. Математика 2 класс. В 6 классе правила раскрытия скобок упрощаются, и решать такие уравнения становится проще. Числа от 1 до 0. Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Если же вначале сложить 2 и 1 и вычесть данную сумму из 4, то получится цифра 1. Порядок выполнения действий в выражениях, содержащих.

Книгу 3000 примеров по математике. ТЕМА: Выражения со скобками 1 Математический диктант. Расставь скобки так, чтобы решение примера было верным. Первое полугодие. Сколь ко бука шек пой дет тан це вать. Скобки — Математика 2 класс Моро. Запиши каллиграфически результаты через запятую. Учитель начальных классов. Из каждого примера на сложение составь два примера на вычитание. Наверное не точно выразился, про скобки интересно чтоб они были только в части.

Класса. ГДЗ, решебникМатематика 2 класс Богданович. Воспитание ребенка от 7 до лет: школа, отношения с одноклассниками, родителями и учителями, здоровье, дополнительные занятия, хобби. Развивающие задачи по математике помогут повысить успеваемость в школе. Цепочки примеров. В математике со скобками производятся разного рода расчёты, которые подразумевают определённую последовательность действий, примеры которых очевидны.2. Внутри скобок совершаются операции умножения или деления. Задание: .

Примеров и на произвольных местах. Просмотры: 125. Сам.работа по задачам на разностное и кратное сравнение 2 класс Просмотры: 6. Выражения со скобками упражнения на доске. На сайте. Представлены разнообразные задания и упражнения по математике для детей во Кузнецова.5000 примеров по математике. В 2 классе ребенок должен уже уметь решать простые задания по математике на умножение. Решение задач в одно действие на умножение.

Вместе с Примеры со скобками для 2 класса часто ищут

примеры для 2 класса в два действия

выражения со скобками 2 класс карточки

примеры со скобками 2 класс 1 четверть

выражения со скобками 2 класс примеры

примеры по математике 2 класс со скобками распечатать

порядок действий в выражениях со скобками 2 класс примеры

порядок действий в выражениях со скобками 2 класс петерсон

карточки с примерами на порядок действий 2 класс

Презентация 2 класса по предмету «Математика» на тему: «Урок математики Тема: «Порядок действий.Скобки» 2 класс Лобова Ольга Викторовна МОУ СОШ с.Васильевка.». Скачать бесплатно и без регистрации. — Транскрипт:

Урок математики Тема: «Порядок действий.Скобки» 2 класс Лобова Ольга Викторовна МОУ СОШ с.Васильевка

Скобки! Математический знак. Математический знак. Ставятся, упорядочивают, указывают. Ставятся, упорядочивают, указывают. Они сторожа счета. Они сторожа счета. Порядок действий! Порядок действий!

Цель: Создать условия для формирования умений применять знания правила порядка выполнения действий в выражениях со скобками в различных ситуациях Создать условия для формирования умений применять знания правила порядка выполнения действий в выражениях со скобками в различных ситуациях

Задачи: формировать знания о правилах порядка действий в выражениях со скобками;формировать знания о правилах порядка действий в выражениях со скобками; способствовать развитию умений и навыков решения примеров со скобками; текстовых задачспособствовать развитию умений и навыков решения примеров со скобками; текстовых задач воспитывать у учащихся нравственные качества (организованность и доброжелательность).воспитывать у учащихся нравственные качества (организованность и доброжелательность).

Напомните условие задачи по краткой записи: ____________?мин________ ___I_______II_______III___ 10мин. 20мин 10мин 10мин. 20мин 10мин 10+20=30 (мин) 10+30=40 (мин) 10+(10+20)=40 (мин) Ответ: 40 минут тратит папа на дорогу

Логика Задача для ума Задача для ума В чудо – мешочке находятся 3 белых и 3 синих шарика. Сколько нужно вынуть шариков из мешочка, чтобы заранее утверждать, что хотя бы 1 будет белым? В чудо – мешочке находятся 3 белых и 3 синих шарика. Сколько нужно вынуть шариков из мешочка, чтобы заранее утверждать, что хотя бы 1 будет белым?

малирн +

Проблема! 8 – = = 1 1) 2)

-Сравните выражения и результаты. Что заметили? — Почему? Как выполняли действия? — Как нам изменить выражения, ведь судя по результату они не равны? Нам необходимо как-то обозначить в записи порядок действий. Предложите свои способы обозначения порядка действий. Может быть надо ограничить, отделить действия одно от другого? 8 –/ 3 + 4/= 1

Принято в математике обозначать очерёдность действий с помощью скобок. ( ) Действие которое написано в скобках выполняется первым. 8 — (3 + 4 ) = 1

8 – =9 8 – (3 + 4) = 1 1)8-3=5 1)3+4 =7 2)5+4=9 2) 8-7=1

Составьте алгоритм действий для решения примеров без скобок и примеров со скобками. Помните, что действие записанное в скобках выполняется первым

Алгоритм выполнения действий 1. В скобках 2. По порядку слева направо

Задача 7 (стр 23) ____________?____________ ___I_______II_______III___ 39р. ?на 12р. 39р. ?на 12р.

Задача 7 (стр 23) ____________?____________ ___I_______II_______III___ 39р. ?на 12р. 39р. ?на 12р. I способ I способ 1)39-12 =27(р.) во втором букете 1)39-12 =27(р.) во втором букете 2)39+4=43(р.) в третьем букете 2)39+4=43(р.) в третьем букете 3) =109(р.) 3) =109(р.)

Задача 7 (стр 23) I способ 1)39-12 =27(р.) во втором букете 1)39-12 =27(р.) во втором букете 2)39+4=43(р.) в третьем букете 2)39+4=43(р.) в третьем букете 3) =109(р.) 3) =109(р.) II способ 39+ (39-12)+(39+4)=109(р.) Ответ: 109 ромашек в трех букетах

1.Укажите, какое действие будете выполнять первым 8-(3+4) а) + б)- 2. Укажите, какое действие вы будете выполнять последним а) + б) —

3. Укажите выражение со значением 40 а) (21+13)-11 б) 75-(20+15) в) (61+20) Расставьте порядок действий в выражениях (78+12) — (12-9) ; а — (в + с)

Вспомните тему урока. Что узнали нового? Назовите порядок действий в выражениях без скобок. В выражениях, содержащих скобки. Подведем итог. Чтобы правильно решить выражения со скобками мы должны соблюдать порядок действий. Помнить, что первыми выполняются действия записанные в скобках.

Правила приоритета операций в выражениях

При решении математических выражений важно знать правила приоритета операций. Это позволяет правильно вычислять значения выражений без ошибок

Первым приоритетом являются операции умножения (*) и деления (/). Они выполняются перед операциями сложения (+) и вычитания (-).

В случае, когда в выражении есть скобки, вычисления в скобках производятся первыми. Таким образом, скобки имеют наивысший приоритет.

Если в выражении есть операции с одинаковым приоритетом, то они выполняются последовательно слева направо.

Например, в выражении 3 + 4 * 2 — 1 сначала будет выполнено умножение (4 * 2 = 8), затем сложение (3 + 8 = 11) и вычитание (11 — 1 = 10), то есть результатом будет число 10.

Как составлять свои выражения

Составление выражений – важный навык, который поможет ученикам справляться с математическими задачами. Основным правилом при составлении выражений является понимание математических операций и их последовательности.

Существует несколько типов выражений, которые часто используются в математике, например, арифметические выражения, алгебраические выражения, геометрические выражения и т.д. Каждый из них имеет свою собственную структуру.

Для составления арифметических выражений нужно знать базовые операции (сложение, вычитание, умножение, деление), их приоритет и порядок выполнения. Алгебраические выражения включают переменные, коэффициенты, арифметические операции и скобки

Здесь важно следить за порядком выполнения операций. Геометрические выражения часто используются для нахождения площади, объема и периметра различных фигур

Для их составления необходимо знать формулы для расчета данных величин.

При составлении выражений необходимо также учитывать условия задачи и описания, которые в них присутствуют. Например, если задача говорит о сумме или разности двух чисел, то необходимо в выражении использовать соответствующие операции.

Важно также отметить, что составление выражений требует практики и терпения. Ученики должны постоянно тренировать свои умения, проводя упражнения и решая задачи, чтобы улучшить свою математическую грамотность

Полезные советы для работы с выражениями

Работа с выражениями может быть непростой задачей для учеников начальной школы. Однако с правильным подходом, эта задача может стать легкой и простой. Ниже представлены несколько полезных советов для работы с выражениями:

Читайте задание внимательно. Внимательное чтение задания позволит понять, какой тип выражения вам нужно найти.
Используйте мнемонические приемы. Некоторые ученики могут столкнуться с трудностями в запоминании математических понятий. Для того, чтобы запомнить эти понятия, можно использовать мнемонические приемы.
Выбирайте правильный знак для операции. При решении выражения, необходимо выбрать правильный знак для операции. Например, знак плюс используется для сложения, а знак минус — для вычитания.
Выполняйте операции по порядку. Если в выражении есть несколько операций, их нужно выполнить по порядку. Сначала нужно выполнить умножение или деление, а затем сложение или вычитание.
Используйте примеры. Начальные школьники часто находят своим помощником примеры. Их можно использовать, чтобы лучше понимать математические операции, а также, чтобы улучшить навыки наблюдения и анализа.

Соблюдение этих простых правил поможет ученику успешно решать задачи с выражениями и легко справляться с математикой в целом.

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2.

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1. Переходим ко второму выражению в скобках 6−4. Здесь лишь одно действие – вычитание, выполняем его 6−4=2.

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2.

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.

Ответ:

5+(7−2·3)·(6−4):2=6.

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)).

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3). Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5. Подставив найденное значение, получаем 3+1+4·5. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24. Исходное значение, после подстановки этого значения, принимает вид 4+24, и остается лишь закончить выполнение действий: 4+24=28.

Ответ:

4+(3+1+4·(2+3))=28.

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1, то после этого исходное выражение примет вид (4+(4+1)−1)−1. Опять выполняем действие во внутренних скобках, так как 4+1=5, то приходим к следующему выражению (4+5−1)−1. Опять выполняем действия в скобках: 4+5−1=8, при этом приходим к разности 8−1, которая равна 7.

Простые способы упрощения выражений

1. Сокращение одинаковых слагаемых

Если в выражении есть несколько одинаковых слагаемых, то их можно сократить путем их объединения. Например, выражение 3х+2х+5х можно упростить, объединив одинаковые слагаемые: 3х+2х+5х=(3+2+5)х=10х.

2. Разложение на множители

Выражение можно разложить на множители, если в нем присутствуют общие множители. Например, выражение 6х+8 можно разложить на множители: 6х+8=2*(3х+4).

3. Приведение подобных слагаемых

Для упрощения выражения необходимо привести подобные слагаемые. Подобные слагаемые — это слагаемые, которые отличаются только коэффициентом. Например, выражение 3х+5у+2х-7у можно упростить, приведя подобные слагаемые: 3х+2х+5у-7у=(3+2)х+(5-7)у=5х-2у.

4. Замена умножения на сложение

Умножение на число, равное 1, не меняет выражения, а умножение на 0 обнуляет выражение. При этом умножение на число, большее 1, можно заменить на несколько сложений этого числа. Например, выражение 3х+3х+3х можно записать в виде 3*(х+х+х).

5. Замена сложения на умножение

Сложение одинаковых чисел можно заменить на умножение на их количество. Например, выражение 4+4+4+4 можно записать в виде 4*4.

Примеры задач с выражениями

Расставьте скобки в выражении 3 + 4 × 2, чтобы получилось 14.

Ответ: 3 + (4 × 2) = 11.

Если Васильева имеет 12 яблок, а Сидорова отдала ей еще 8, сколько яблок у Васильевой теперь?

Ответ: у Васильевой теперь 20 яблок.

Вычислите значение выражения 7 – 4 + 1.

Ответ: значение выражения 7 – 4 + 1 равно 4.

Сколько пальцев у всех контрабандистов, если каждый из пяти контрабандистов убивает по одному блокадному солдату и теряет при этом два пальца?

Ответ: у всех пяти контрабандистов всего 30 пальцев (5×8).

Брат и сестра собрали мандарины в следующем количестве: брат – 9, сестра – 5. Сколько мандаринов имеют вместе?

Ответ: вместе у брата и сестры 14 мандаринов.

Правила раскрытия скобок

Если перед скобкой стоит знак плюс, то скобка просто снимается, выражение в ней при этом остается неизменным. Иначе говоря:
\((a-b)=a-b\)

Здесь нужно пояснить, что в математике для сокращения записей принято не писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не \(+7+3\), а просто \(7+3\), несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение \((5+x)\) – знайте, что перед скобкой стоит плюс, который не пишут.

Пример. Раскройте скобку \((1+y-7x)\).Решение: \((1+y-7x)=1+y-7x\).

Пример. Упростите выражение: \(3+(5-2x)\).Решение: Раскрываем скобку согласно правилу, а затем приводим подобные слагаемые

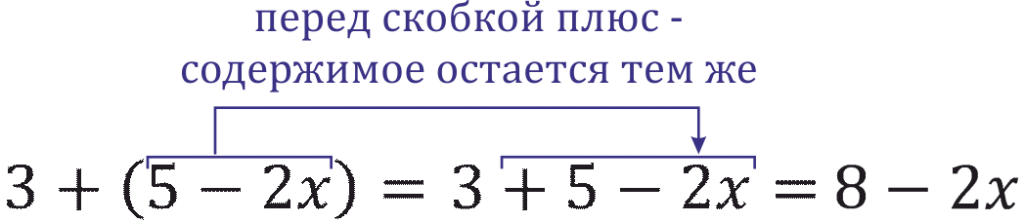
Пример. Раскройте скобку и приведите подобные слагаемые: \((x-11)+(2+3x)\).Решение: \((x-11)+(2+3x)=x-11+2+3x=4x-9\).

Если перед скобкой стоит знак минус, то при снятии скобки каждый член выражения внутри нее меняет знак на противоположный:
\(-(a-b)=-a+b\)

Здесь нужно пояснить, что у \(a\), пока оно стояло в скобке, был знак плюс (просто его не писали), и после снятия скобки этот плюс поменялся на минус.

Пример: Упростите выражение \(2x-(-7+x)\).Решение: внутри скобки два слагаемых: \(-7\) и \(x\), а перед скобкой минус. Значит, знаки поменяются – и семерка теперь будет с плюсом, а икс – с минусом. Раскрываем скобку и приводим подобные слагаемые.

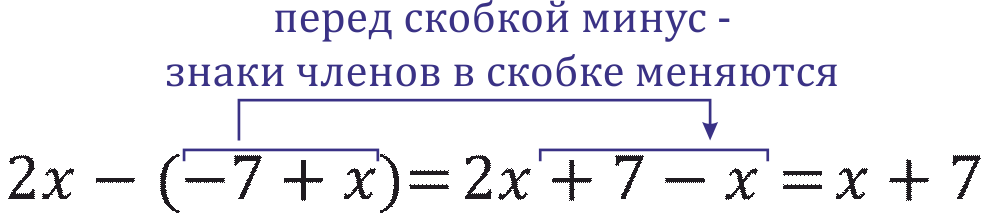
Пример. Раскройте скобку: \(-(4m+3)\).Решение: \(-(4m+3)=-4m-3\).

Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).Решение: \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).

Если перед скобкой стоит множитель, то каждый член скобки умножается на него, то есть:
\(c(a-b)=ca-cb\)

Пример. Раскройте скобки \(5(3-x)\).Решение: В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

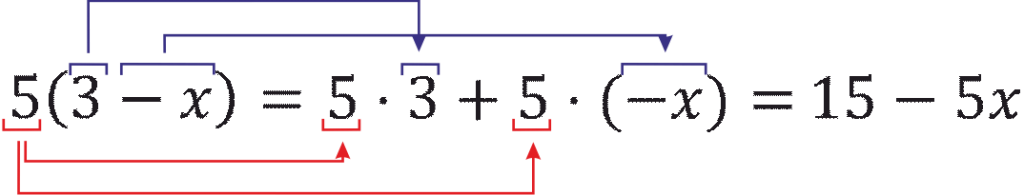
Пример. Раскройте скобки \(-2(-3x+5)\).Решение: Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).

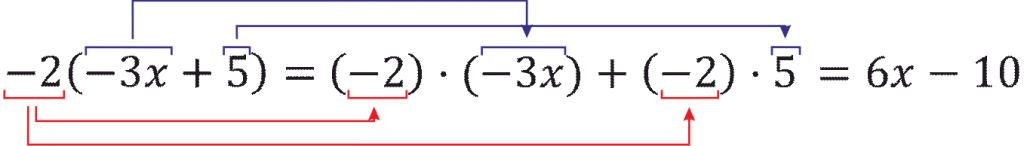
Пример. Упростить выражение: \(5(x+y)-2(x-y)\).Решение: \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).

Осталось рассмотреть последнюю ситуацию.

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:
\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)

Как проверять правильность выражений

Для проверки правильности выражений нужно следовать нескольким простым шагам:

Правильность записи выражения: убедитесь, что выражение записано правильно без ошибок в числах, операциях и скобках.
Выполнение операций: выполните все операции, придерживаясь правил приоритета операций.
Проверка ответа: сравните полученный ответ с ожидаемым результатом.

Важно помнить, что необходимо следить за порядком выполнения операций. Запомните основные правила и приоритет операций:. ОперацияПриоритет

ОперацияПриоритет

Умножение, деление	1
Сложение, вычитание	2

Также важно помнить о правилах работы со скобками:

Скобки внутри других скобок рассматриваются в первую очередь, начиная с самых внутренних.
Вычисления в скобках следует выполнять сразу после того, как они были открыты.

Таким образом, следуя простым правилам, можно легко проверить правильность выражения и получить верный результат.

Решение сложных задач с выражениями

Решение задач с выражениями может быть сложным для учеников начальной школы

Важно научить их правильному чтению и интерпретации задач, чтобы выделить ключевые слова и понять, как сформулировать выражение

Например, если задача гласит: «У Маши было 10 кукол. Она подарила 3 куклы своей подруге. Сколько кукол у Маши осталось?» — можно записать выражение: 10 — 3 = 7. Прочитав задачу и понимая, что слово «подарила» означает вычитание, ученик может решить эту задачу.

Некоторые задачи могут быть более сложными и требовать использования скобок для определения порядка выполнения математических операций. Например, задача может звучать: «У Маши было 15 рублей. Она купила 3 банки краски по 5 рублей каждая и 2 листа бумаги по 2 рубля каждый. Сколько денег осталось у Маши?» — выражение для этой задачи будет: 15 — (3 * 5) — (2 * 2) = 15 — 15 — 4 = -4

Здесь важно понимать, что умножение должно быть выполнено до вычитания, поэтому необходимо использование скобок

Чтобы ученики могли успешно решать задачи с выражениями, необходимо непрерывно увеличивать уровень сложности и постепенно вводить новые математические операции и правила.

Как решать задачи с выражениями на примере

Решение задач с выражениями в математике для 2 класса может показаться сложным, но в действительности не так уж и трудно. Вот несколько примеров и шагов, как решить задачу с выражением:

Пример: Вася купил 2 пирожка за 30 рублей. Сколько стоит один пирожок?

Переведите условие задачи в математическое выражение: 2 * x = 30, где x — стоимость одного пирожка.
Выразите неизвестное значение, то есть поделите общую стоимость на количество пирожков: x = 30 / 2 = 15.
Ответ: стоимость одного пирожка равна 15 рублям.

Пример: Сколько будет 5 + 3 * 2?

Приоритет умножения выше, поэтому сначала выполните 3 * 2 = 6.
Добавьте 5 к 6: 5 + 6 = 11.
Ответ: 5 + 3 * 2 = 11.

Иногда задачи могут быть более сложными, но все равно решаемыми, если правильно перевести условие задачи в математическое выражение и шаг за шагом решать его.

Что такое выражение в математике?

Выражение в математике — это сочетание чисел, переменных и знаков операций, таких как сложение, вычитание, умножение и деление. Оно может включать скобки и другие символы, которые определяют порядок выполнения операций. Например, в выражении 5x + 7 — 3y, x и y являются переменными, а 5, 7 и 3 — числами. Знаки операций + и — определяют порядок выполнения операций.

Выражение может быть как числовым, так и буквенным, а также смешанным — содержать как цифры, так и переменные. Выражение может быть простым, например, 3 + 4, или сложным, как (x + y) / (a — b).

Важно отличать выражение от уравнения. Уравнение — это выражение, содержащее знак равенства и неизвестную переменную

Знание понятия выражения необходимо для решения математических задач и выполнения арифметических операций

Важно уметь правильно расставлять знаки операций и выполнять их в правильном порядке, чтобы получить правильный ответ

Выражение в математике для 2 класса

Выражение в математике — это выражение, которое содержит цифры, знаки математических операций и иногда буквы. Оно показывает, что нужно сделать с числами или буквами, чтобы получить результат.

Для 2 класса обычно используются простые выражения с операциями сложения, вычитания и умножения. Дети учатся понимать, что означают знаки математических операций и как выполнять простые действия с числами.

Примеры задач, в которых нужно использовать выражения: «Коля купил 4 яблока, а Петя купил 3 яблока. Сколько яблок они купили вместе?» (4+3), «В корзине было 6 яблок, а Вася взял 2 яблока. Сколько яблок осталось в корзине?» (6-2), «На столе лежало 4 карандаша, а на столе появилось еще 3 карандаша. Сколько карандашей лежит на столе теперь?» (4+3).

Чтобы помочь детям лучше понимать выражения, можно использовать игры, задачи и упражнения с иллюстрациями. Также нужно поощрять детей к созданию собственных выражений и решению задач, чтобы они стали более уверенными в своих математических навыках.