Формулы сокращенного умножения с примерами

Тригонометрия

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

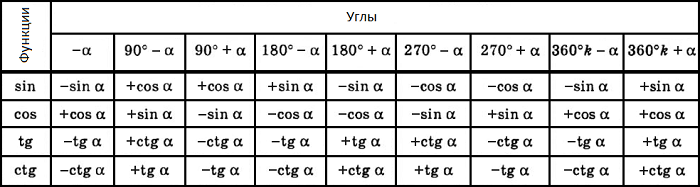
Формулы приведения задаются в виде таблицы:

Основные математические формулы

Здесь вы найдете исчерпывающий список основных математических формул, обычно используемых при выполнении основных математических вычислений.

_{1 2 3 n}

Процент:

Процент в дробь: x% = x/100

Формула процента: Ставка/100 = процент/основание

Ставка: процент. База: Сумма, от которой вы берете процент. Процент: Ответ, полученный путем умножения основания на скорость

Формулы дробей:

Преобразование неправильной дроби в смешанное число:

Формула пропорции:

В пропорции произведение крайностей (ad) равно произведению средних (bc),

Таким образом, ad = bc

Математические формулы для потребителей:

Скидка = прейскурантная цена × ставка дисконта

Цена продажи = прейскурантная цена − скидка

Ставка дисконтирования = скидка ÷ прейскурантная цена

Налог с продаж = цена товара × налоговая ставка

Проценты = основная сумма × процентная ставка × время

Чаевые = стоимость еды × ставка чаевых

Комиссия = стоимость обслуживания × ставка комиссии

Геометрические формулы:

Периметр :

Периметр квадрата : s + s + s + s s: длина одной стороны

Периметр прямоугольника : l + w + l + w l: длина: ширина

Периметр треугольника : a + b + c

Площадь:

Площадь квадрата : s × s s: длина одной стороны

Площадь a прямоугольник : l × w l: длина w: ширина

Площадь треугольника : (b × h)/2 b: длина основания h: длина высоты

Площадь трапеции : (b ₁ + b ₂ ) × h/2 b ₁ и b ₂ : параллельные стороны или основания h: длина высота

объем:

объем куба : s × s × s s: длина одной стороны

объем коробки : l × w5 l : 9003 длина w: ширина h: высота

Объем сферы : (4/3) × pi × r 3 pi: 3,14 r: радиус сферы

Объем треугольной призмы : площадь треугольника × высота = (1/2 основания × высота) × высота основание: длина основания треугольника height: высота треугольника Height: высота треугольной призмы

Объем цилиндра :pi × r 2 × высота pi: 3,14 r: радиус окружности основания Высота: высота цилиндра

Есть вопросы по основным математическим формулам? Отправить мне письмо здесь
и задайте мне любые вопросы об этих основных математических формулах

1. Квадратичная формула: простые шаги

   26, 23 января 11:44

   Узнайте о квадратичной формуле, дискриминанте, важных определениях, связанных с формулой, и приложениях.

   Подробнее

2. Формула площади — список важных формул

   25, 23 января 05:54

   Что такое формула площади для двумерной фигуры? Вот список тех, которые вы должны знать!

   Подробнее

Переместительный закон сложения

Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:

5 + 2 = 7

2 + 5 = 7

Если на одну чашу весов положить пакет, в котором 10 килограмм яблок, и на другую чашу так же положить пакет, в котором 10 килограмм яблок, то весы выровнятся, и не важно что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм

От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес

Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.

Таким образом,  между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:

5 + 2 = 2 + 5

7 = 7

Полагаем что вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:

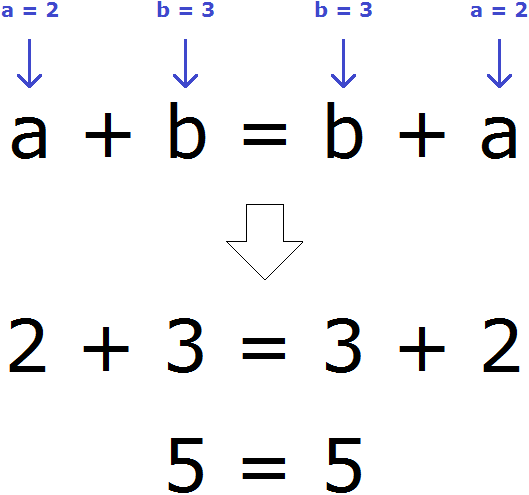
a + b = b + a

Записанный переместительный закон сложения будет работать для любых чисел. Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b

Арифметическая прогрессия

Определение арифметической прогрессии

Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом d, называют арифметической прогрессией. Число d называют разностью арифметической прогрессии. В арифметической прогрессии {a_n}, т. е. в арифметической прогрессии с членами:  a₁, a₂, a₃, a₄, a₅, …, a_n-1, a_n, …   по определению:  a₂=a₁+d; a₃=a₂+d; a₄=a₃+d; a₅=a₄+d; …; a_n=a_n-1+d; …

Свойства арифметической прогрессии

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов:

a_n=(a_n-1+a_n+1):2;

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому равноотстоящих от него членов:

a_n=(a_n-k+a_n+k):2.

Преобразование (конструирование) графиков функций

• График функции y=- f(x) получается из графика функции y=f (x) зеркальным отражением от оси абсцисс.
• График функции y=|f(x)| получается зеркальным отражением от оси абсцисс той части графика функции y=f (x), которая лежит ниже оси абсцисс.
• График функции y=f(|x|) получается из графика функции y=f (x) следующим образом: оставляют часть графика справа от оси ординат и отображают эту же часть симметрично ей самой относительно оси ординат.
• График функции y=A∙f(x) получается из графика функции y=f (x) растяжением в А раз вдоль оси ординат. (Ордината каждой точки графика функции y=f (x) умножается на число А).
•  График функции y=f(k∙x) получается из графика функции y=f (x) сжатием в k раз при k > 1 или растяжением в k раз при 0
•  График функции y=f(x- m) получается из графика функции y=f (x) параллельным переносом на m единичных отрезков вдоль оси абсцисс.
•  График функции y=f(x)+n получается из графика функции y=f (x) параллельным переносом на n единичных отрезков вдоль оси ординат.

Квадратное уравнение

Определение. Уравнение вида ax2+bx+c=0, где a, b и c – любые действительные числа, причем а≠0, х – переменная, называется квадратным уравнением.

a – первый коэффициент, b – второй коэффициент, c – свободный член.

Решение неполных квадратных уравнений 

• ax2=0 – неполное квадратное уравнение (b=0, c=0). Решение: х=0. Ответ: 0.
• ax2+bx=0 – неполное квадратное уравнение (с=0). Решение: x (ax+b)=0 → x₁=0 или ax+b=0 → x₂=-b/a. Ответ: 0; -b/a.
• ax2+c=0 – неполное квадратное уравнение (b=0); Решение: ax2=-c → x2=-c/a.

Если (-c/a) , то действительных корней нет. Если (-с/а) > 0, то имеем два действительных корня:

Решение полных квадратных уравнений

 ax2+bx+c=0 – квадратное уравнение общего вида 

Дискриминант D=b2— 4ac.

Если D > 0, то имеем два действительных корня:

Если D=0, то имеем единственный корень (или два равных корня) х=-b/(2a).

Если D

 ax2+bx+c=0 – квадратное уравнение частного вида при четном втором

 коэффициенте b

 ax2+bx+c=0 – квадратное уравнение частного вида при условии: a-b+c=0. 

Первый корень всегда равен минус единице, а второй корень равен минус с, деленному на а:

x₁=-1, x₂=-c/a.

 ax2+bx+c=0 – квадратное уравнение частного вида при условии: a+b+c=0. 

Первый корень всегда равен единице, а второй корень равен с, деленному на а:

x₁=1, x₂=c/a.

Решение приведенных квадратных уравнений

x2+px+q=0 – приведенное квадратное уравнение (первый коэффициент равен единице).

Приведенные квадратные уравнения можно решать по тем же формулам, что и полные квадратные уравнения, однако, чаще для решения приведенных квадратных уравнений применяют теорему Виета.

Теорема Виета

Сумма корней приведенного квадратного уравнения x2+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

x₁+x₂=-p;  x₁∙x₂=q.

Теорема Виета для полного квадратного уравнения ax2+bx+c=0.

Сумма корней равна минус b, деленному на а, произведение корней равно с, деленному на а:

x₁+x₂=-b/a;  x₁∙x₂=c/a.

Стандартный вид числа.

Очень большие и очень малые числа принято записывать в стандартном виде: a∙10n, где 1≤а  и n  (натуральное или целое) – есть порядок числа, записанного в стандартном виде.

•  Выражения, которые составлены из чисел, переменных и их степеней, при помощи действия умножения называются одночленами.
•  Такой вид одночлена, когда на первом месте стоит числовой множитель (коэффициент), а за ним переменные с их степенями, называют стандартным видом одночлена. Сумму показателей степеней всех переменных, входящих в состав одночлена, называют степенью одночлена.
•  Одночлены, имеющие одинаковую буквенную часть, называются подобными одночленами.

Логарифм числа b по основанию a

Логарифмом числа b по основанию а (log_ab)  называют показатель степени, в которую нужно  возвести число а, чтобы получить число b.

log_ab=n, если an=b. Примеры: 1) log₂8=3, т. к. 23=8;

2) log₅(1/25)=-2, т. к. 5-2=1/52=1/25;                         3) log₇1=, т. к. 7=1.

Под знаком логарифма могут быть только положительные числа, причем, основание логарифма — число а≠1. Значением логарифма может быть любое число.

Основное логарифмическое тождество

Это тождество следует из определения логарифма: так как логарифм – это показатель степени (n), то, возводя в эту степень число а, получим число b.

Примеры.

Десятичный логарифм

Логарифм по основанию 10 называют десятичным логарифмом и при написании опускают основание 10 и букву «о» в написании слова «log».

lg7=log₁₀7,        lg7 – десятичный логарифм числа 7.

Натуральный логарифм

Логарифм по основанию е (Неперово число е≈2,7) называют натуральным логарифмом.

ln7=log_e7,          ln7 – натуральный логарифм числа 7.

Свойства логарифмов справедливы для логарифмов по любому основанию.

log_a(x∙y)=log_ax+log_ay

Логарифм произведения равен сумме логарифмов сомножителей.

Логарифм частного

log_a(xy)=log_ax— log_ay

Логарифм частного равен разности логарифмов делимого и делителя.

Основание логарифма и число под знаком логарифма можно поменять местами по формуле:

log_ab=1log_ba   Логарифм числа b по основанию а равен единице, деленной на логарифм числа а по основанию b.

Общая формула перехода к логарифму по другому основанию

log_ab=log_cb/log_ca

Логарифм числа b по основанию а равен  логарифму числа b по новому основанию с, деленному на логарифм старого основания а по новому основанию с.

log_abk=k∙log_ab    Логарифм степени (bk) равен произведению показателя степени (k) на логарифм основания (b) этой степени.

Логарифм числа br по основанию ar.

log_arbr=log_ab   или  log_ab=log_arbr

Значение логарифма не изменится, если основание логарифма и число под знаком логарифма возвести в одну и ту же степень.

Правило встречается в следующих упражнениях:

1 класс

Страница 8. Урок 5,
Петерсон, Учебник, часть 2

Страница 43. Урок 22,
Петерсон, Учебник, часть 2

Страница 45. Урок 23,
Петерсон, Учебник, часть 2

Страница 49. Урок 25,
Петерсон, Учебник, часть 2

Страница 9. Урок 5,
Петерсон, Учебник, часть 3

Страница 15. Урок 8,
Петерсон, Учебник, часть 3

Страница 22. Урок 12,
Петерсон, Учебник, часть 3

Страница 29. Урок 15,
Петерсон, Учебник, часть 3

Страница 35. Урок 18,
Петерсон, Учебник, часть 3

Страница 44. Урок 23,
Петерсон, Учебник, часть 3

2 класс

Страница 41,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 55,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 33,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 48,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 36. ПР 5. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 4. Урок 1,
Петерсон, Учебник, часть 2

Страница 45. Урок 17,
Петерсон, Учебник, часть 2

Страница 100. Повторение,
Петерсон, Учебник, часть 3

Страница 104. Повторение,
Петерсон, Учебник, часть 3

Задание 106. Повторение,
Петерсон, Учебник, часть 3

3 класс

Страница 57,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 70,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 107,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 17. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 22. Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 11. Урок 3,
Петерсон, Учебник, часть 1

Страница 18. Урок 6,
Петерсон, Учебник, часть 1

Страница 93. Урок 35,
Петерсон, Учебник, часть 1

Страница 21. Урок 9,
Петерсон, Учебник, часть 2

4 класс

Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 60,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 5. ПР. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 74,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 27. Урок 9,
Петерсон, Учебник, часть 1

5 класс

Задание 429,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1334,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1534,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 922,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

Номер 244,
Мерзляк, Полонский, Якир, Учебник

Номер 254,
Мерзляк, Полонский, Якир, Учебник

Номер 255,
Мерзляк, Полонский, Якир, Учебник

Номер 256,
Мерзляк, Полонский, Якир, Учебник

Номер 432,
Мерзляк, Полонский, Якир, Учебник

Номер 1127,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 331,
Мерзляк, Полонский, Якир, Учебник

Номер 401,
Мерзляк, Полонский, Якир, Учебник

Номер 967,
Мерзляк, Полонский, Якир, Учебник

Номер 981,
Мерзляк, Полонский, Якир, Учебник

Номер 1037,
Мерзляк, Полонский, Якир, Учебник

Номер 1064,
Мерзляк, Полонский, Якир, Учебник

Номер 1096,
Мерзляк, Полонский, Якир, Учебник

Номер 1097,
Мерзляк, Полонский, Якир, Учебник

Номер 1106,
Мерзляк, Полонский, Якир, Учебник

Задание 1118,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 315,
Мерзляк, Полонский, Якир, Учебник

Номер 316,
Мерзляк, Полонский, Якир, Учебник

Номер 480,
Мерзляк, Полонский, Якир, Учебник

Номер 481,
Мерзляк, Полонский, Якир, Учебник

Номер 906,
Мерзляк, Полонский, Якир, Учебник

Номер 1040,
Мерзляк, Полонский, Якир, Учебник

Номер 1071,
Мерзляк, Полонский, Якир, Учебник

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Номер 3,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Номер 46,
Мерзляк, Полонский, Якир, Учебник

Номер 47,
Мерзляк, Полонский, Якир, Учебник

Номер 229,
Мерзляк, Полонский, Якир, Учебник

Номер 391,
Мерзляк, Полонский, Якир, Учебник

Номер 392,
Мерзляк, Полонский, Якир, Учебник

Урок математики 3 класс. Л.Г.Петерсон. Тема “Формула работы”

I. Организационный момент.

– Сейчас урок математики.

II. Мотивация к учебной деятельности.

– Давайте прочитаем хором высказывание

Человек лишь тогда чего-то добивается, когда он верит в свои силы. (немецкий философ Андреас Фейербах)

– О каких качествах идет речь?

– Как эти качества могут нам пригодиться?

III. Актуализация знаний.

– В математике часто используются формулы.

– Какие формулы вы знаете?

– А зачем они нужны? (Чтобы решать похожие и обратные задачи)

– Рассмотрите таблицу. О каких величинах можно составить задачи.

– Составьте задачи по данным таблицы.

s	v	t
	60 км/ч	4ч
540 км		6ч
57км	19км/ч

S=v•t t=s:v v=a•b•c s= a•b v=s:t

– Какие формулы вы будете использовать для решения этих задач? Подчеркнем их и прочитаем.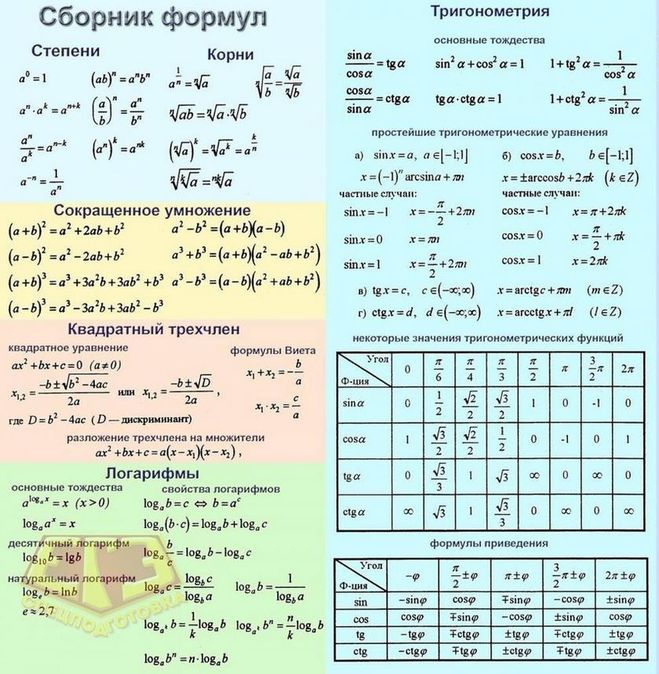

– Запишите в тетради только ответы этих задач.

– Давайте проверим с помощью сигнальных кругов.

-Те, кто не ошибся в решении задач, поставьте на полях +.

IV. Пробное действие.

– Запишите формулу, для решения следующей задачи.

«Одна швея за 5ч сшила 20 фартуков, другая за 4ч сшила 16 таких же фартуков. Какая швея работает быстрее?»

– Какие формулы записали? А кто не записал никакой формулы?

– В чем трудность? (Не могу записать формулу для такой задачи)

– Почему возникло затруднение? (Не знаем такой формулы)

– О чем эта задача? (о работе)

– Какие величины есть в задаче? (время работы, скорость работы)

– Какая новая величина? (работа)

– Как же можно назвать эту формулу? (формула работы)

V.Сообщение темы урока и постановка целей.

– Итак тема урока «Формула работы»

– Какие же цели мы поставим на сегодняшний урок?

Цели урока:

1. Узнать формулу работы.

2. Научиться решать задачи по формуле работы.

VI. Решение учебной задачи. Открытие нового знания.

– Заполнимтаблицу к задаче.

– О каких величинах идет речь в этой задаче?

(о времени, количестве выполненной работы)

– Если сказано «быстрей», то о какой величине идет речь?

– Какие задачи напоминает? (задачи на движение)

– Как же найти скорость работы? (всю работу разделить на время)

– В математике скорость работы принято обозначать v, так же, как и в задачах на движение.

Вся выполненная работа – А,

Время, затраченное на работу – t, так же, как и в задачах на движение.

– Попробуйте сами записать формулу, по которой можно найти скорость работы.v=At

– А теперь выведем формулу работы.

– Чем является А? (А – делимое, чтобы найти делимое, нужно частное умножить на делитель)

– Прочитайте получившуюся формулу.A=v•t

– Какую еще формулу можно вывести?t= Av

– А теперь сверим с текстом на доске.

– Что нового узнали, почитав текст?

(Скорость еще называют производительностью)

– Что же мы подразумеваем под словом работа?

VII. Физминутка.

– Объясните, как вы понимаете смысл следующих высказываний? (с. 44 № 1)

– Давайте еще раз озвучим цели урока.

– Узнали формулу работы? Прочитайте ее.

– Какие формулы вывели?Прочитайтеих.

VIII. Первичное закрепление.

– Какой была вторая цель?

(Научиться решать задачи по формуле работы.)

– Предлагаю выполнить следующие задания:

1.  Составить и решить задачи по таблице.

A	v	t
	4 детали/мин	5 мин
160 скворечников		8 дней
120 шт.	60 шт/ч

A=v•tv=Att= Av

– Запишите решение этих задач.

-Проверим решение задач через документ-камеру.

– Какую формулы выбрали для решения задач?

– Покажите, какую формулу использовали для нахождения неизвестной величины.

– Те, кто не ошибся в решении задач, поставьте на полях +.

2. Практическая работа (индивидуальные карточки с примерами)

– А сейчас вы попробуете вычислить производительность своего умственного труда.

– Будем решать на время примеры, а данные заносить в таблицу.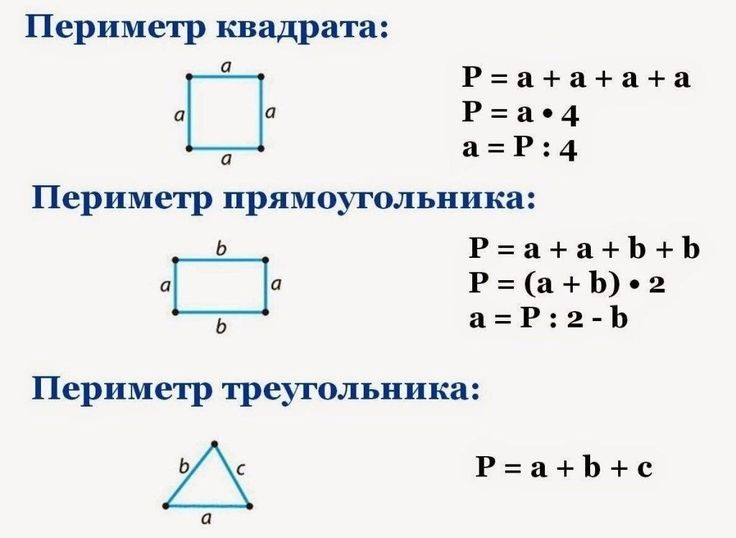

Вся работа A	Производительность V	Время работы t
…		2мин

3. Взаимопроверка

– Давайте проверим правильность решения.

– Запишите количество правильных ответов в таблицу.

– Если количество правильных ответов не меньше 10 – поставьте себе +

– Как узнать производительность? Какой формулой воспользуемся?(v=A: t)

– Вычислите свою производительность.

(количество правильных примеров разделить на 2 мин)

-Где в жизни может пригодиться умение находить производительность, объем работы, время работы?

IX. Контроль достижения целей.

– А теперь вернемся к задаче, которая вызвала затруднение.

– Какую же формулу выберем?

– Запишите самостоятельно решение этой задачи в тетрадь.

– Проверим решение.

– Те, кто правильно решил задачу, поставьте на полях +.

X. Рефлексия.

– Итак, какой была тема урока?

– Какие цели мы поставили на урок? Прочитайте формулу работы.

– Достигли этих целей?

– Помогли ли нам в достижении поставленных целей те качества, о которых мы говорили в начале урока.?

XI. Д/з с. 44 № 4, № 5.

Основные формулы математики

Основными формулами математики считаются формулы быстрого умножения. Их не так много, поэтому лучше все заучить наизусть. Всего формул семь, каждая из них была выведена, для облегчения счета. Заучивают формулы в 4 этапа.

Первыми идут формулы суммы и разности квадратов. Формулу суммы мы уже знаем.

$$(a+b)^2=a^2+2ab+b^2$$

Квадрат разности не сильно отличается.

$$(a-b)^2=a^2-2ab+b^2$$

Знак минуса вполне логичен, и его достаточно просто запомнить.

Следующими запоминают куб суммы и куб разности. Они учатся быстрее, просто запоминаясь по аналогии.

$$(a+b)^3=a^3+3a^2*b+3a*b^2+b^3$$

$$(a-b)^3=a^3-3a^2*b+3a*b^2-b^3$$

Дальше идут формулы суммы и разности кубов, а так же разность квадратов. Разность квадратов записывается достаточно легко.

$a^2+b^2=(a+b)(a-b)$ – а вот формулы суммы квадратов нет. В начале курса 5 класса по математике ученики очень часто путаются формулы квадрата разности и разности квадратов. Попробуем научиться их различать.

Что такое разность квадратов? Это два числа в квадрате, из одного вычитается другое. А что такое квадрат разности? Из одного числа вычли другое, а результат возвели в квадрат. Достаточно один раз запомнить, а лучше понять, это объяснение и проблем с этими двумя формулами не будет никогда.

Следующими и последними идут формулы суммы и разности кубов. Они немного сложнее и для облегчения их запоминания придумали понятие неполного квадрата суммы и неполного квадрата разности.

Вспомним формулу квадрата суммы.

$$(a+b)^2=a^2+2ab+b^2$$

Обратим внимание на вторую часть. $$a^2+2ab+b^2$$ – это и называется полным квадратом суммы

А неполным называется выражение:

$$a^2+2ab+b^2$$ – это и называется полным квадратом суммы. А неполным называется выражение:

$$a^2+ab+b^2$$. Это легко запомнить. По аналогии неполный квадрат разности: $a^2-ab+b^2$.

Теперь приведем формулы суммы и разности кубов.

$$a^3+b^3=(a+b)( a^2-ab+b^2)$$ – сумма кубов это произведение суммы чисел на неполный квадрат разности этих чисел.

$$a^3+b^3=(a-b)( a^2+ab+b^2)$$ – разность кубов это произведение разности чисел на квадрат суммы этих чисел.

Как показывает практика, последние две формулы проще запомнить в словесной форме. К тому же эти формулы часто встречаются при решении простых уравнений. Поэтому, дабы не бежать каждый раз в интернет – проще их запомнить.

Что мы узнали?

Мы дали определение понятию формулы, привели основные формулы математики и обозначили, что формулой можно пользоваться в обе стороны от знака равенства.

1. /5

   Вопрос 1 из 5

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число или число на сумму.

Рассмотрим следующее выражение:

(3 + 5) × 2

Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:

(3 + 5) = 8

В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:

8 × 2 = 16

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:

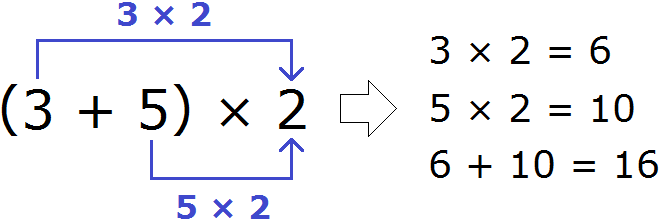
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:

(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16

Или ещё короче:

(3 + 5) × 2 = 6 + 10 = 16

Теперь запишем распределительный закон умножения с помощью переменных:

(a + b) × c = a × c + b × c

Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.

Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×

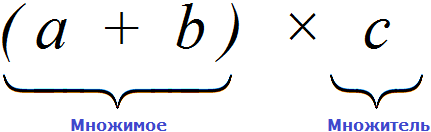
Из мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:

c × (a + b) = c × a + c × b

Пример 2. Найти значение выражения 5 × (3 + 2)

Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:

5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25

Пример 3. Найти значение выражения 6 × (5 + 2)

Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:

6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42

Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.

Пример 4. Найти значение выражения 5 × (6 − 2)

Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20

Пример 5. Найти значение выражения 7 × (3 − 2)

Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7