Основные задачи и действия на обыкновенные дроби

Содержание

• Слайд 1

  Действия над ними

• Слайд 2

  В жизни нам нередко приходится пользоваться не только целыми числами, но и их частями (долями).Доли — это равные части целого.

  Число, стоящее над дробной чертой, называется числителем. Числитель показывает, сколько долей взяли (закрасили) у целого.
  Число, стоящее под дробной чертой, называется знаменателем. Знаменатель показывает, на сколько равных долей разделено целое.

• Слайд 3

  Некоторые обыкновенные дроби имеют особые названия. Знать, как называются такие дроби, надо наизусть.

• Слайд 4

  С помощью дробей одну и ту же часть целого предмета можно записать разными способами.

  А чтобы получить 4/8, мы числитель и знаменатель 1/2 умножили на 4.
  Дробь 2/4 мы получили из дроби 1/2, умножив её числитель и знаменатель на 2.

• Слайд 5

  Дробь, равную данной, можно получить, если числитель и знаменатель дроби одновременно разделить на одно и то же число, не равное нулю.Такое преобразование дроби называют сокращением дроби.

  Сокращение дроби обычно записывают следующим образом.
  Числитель и знаменатель зачёркиваются чёрточками, и рядом с ними записываются результаты деления (частные) числителя и знаменателя на одно и то же число.
  Число, на которое делили числитель и знаменатель, держим в уме.

• Слайд 6

  Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
  Запишем это свойство в виде буквенных выражений.
  ,где a, b и k — натуральные числа.

• Слайд 7

  Сравнение дробей с одинаковыми числителями
  Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

• Слайд 8

  Правило выше легче понять, если представить, что у вас в руках куски торта. В первом случае торт разделили на 2 части (знаменатель дроби равен 2), и у вас в руках половина торта, а во втором — торт поделили на 8 частей, и у вас в руках маленькая часть торта.

• Слайд 9

  Сложение дробей с одинаковыми знаменателями

  Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.
  Пример.

  Вычитание дробей с одинаковыми знаменателями
  При вычитании дробей
  с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.
  Пример.

• Слайд 10

  Вычитание правильной дроби из единицы

  Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.
  Пример.

  Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную дробь 7/7 и вычитают по правилу вычитания дробей с одинаковыми знаменателями.

• Слайд 11

  Чтобы найти дробь (часть) от числа, нужно это число умножить на данную дробь
  Пример. Рассмотрим задачу.
  В книге 160 страниц. Юра прочитал 4/5 книги. Сколько страниц прочитал Юра?
  Прежде всего найдём в задаче целое. Это — вся книга и в ней всего 160 страниц.
  Посмотрим на дробь (часть) от целого: 4/5. Знаменатель равен 5, значит, целое разделили на 5 частей и мы можем найти сколько страниц составляет 1/5 часть.
  Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.

• Слайд 12

  Если известно сколько составляет часть от целого, то по известной части можно «восстановить» целое.

  Чтобы найти число по его части, выраженной дробью, нужно данное число разделитьна дробь.
  Пример. Рассмотрим задачу.
  Поезд прошёл 240 км, что составило 15/23 всего пути. Какой путь должен пройти поезд?
  Решение. 240 км — часть всего пути. Эти же километры выражены дробью 15/23 от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части, и 15 таких частей составляют 240 км (числитель дроби равен 15).
  Значит, можно найти, сколько составляет 1/23 часть пути.
  240 : 15 = 16 (км).
  Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью 23/23.
  Значит, чтобы найти весь путь (23 части, каждая из которых по 16 км) нужно:
  16 • 23 = 368 (км)
  Кратко запись решения такой задачи можно сделать следующим образом.

• Слайд 13

  Математическую операцию деление вы уже знаете хорошо. До сих пор мы делили большее число на меньшее, а можно ли меньшее число разделить на большее. Рассмотрим пример из жизни. 

• Слайд 14

  ПРИ ДЕЛЕНИИ МЕНЬШЕГО НАТУРАЛЬНОГО ЧИСЛА НА БОЛЬШЕЕ, МЫ ПОЛУЧАЕМ ДРОБЬ, ГДЕ В ЧИСЛИТЕЛЕ ЗАПИСАНО ДЕЛИМОЕ, А В ЗНАМЕНАТЕЛЕ ДЕЛИТЕЛЬ

• Слайд 15

Посмотреть все слайды

Урок математики в 4 классе «Решение задач на нахождение числа по дроби и дроби по числу»

Тема урока: «Решение задач на нахождение числа по дроби и дроби по числу»

Цели урока: 1.Учиться решать задачи на нахождение числа по дроби и дроби по числу.

2. Повторить и закрепить сложение, вычитание, умножение и деление

многозначных чисел, решение составных уравнений.

3

Развивать внимание, мышление, воображение, речь, память, интерес. к математике

к математике.

Оборудование: числовое табло; цветные таблицы на развитие логического мышления,

периметра и площади.

Ход урока

1. Организационный момент

2. Актуализация знаний

1.Сведения о Республике Марий Эл

На карте России наша республика занимает небольшую площадь – 23000 кв. км.Протяженность Республики Марий Эл с запада на восток – 275 км.

Протяженность с севера на юг – 150 км.

Общая длина границ – 1200 км.

Протяженность всех рек республики – 7500 км.

Население Республики Марий Эл на 1 января 2009 г. – 700 000 человек.

23000 275 150 1200 7500 700 000

• Что можно сказать о числах? / Кратны 5/

• Какое число лишнее? Почему? / 275, оно не круглое/

• По какому принципу можно провести классификацию / 6, 5, 4, 3-х значные числа/

2. Высота полета птиц:

• Лебеди, журавли – 2400 м

• Кряква – 6300 м

• Коноплянка — 3000 м

• Орлы – 6000 м

• Грифы – 6900 м

2400 6300 3000 6000 6900 Найдите 1% от каждого числа.

24 63 30 60 69 Найдите 1/3 от этих чисел.

8 21 10 29 23

3. Запишите меры массы в порядке убывания

Т Ц КГ Г

10 100 1000

• Какие старинные меры массы вы знаете? / пуд, фунт и т.д./

• Найдите дробь от числа: 1/5 от 1т, ½ от 1ц, 1/10 от 1кг

2ц 50кг 100г Какие это числа? / 1, 2, 3-х значные, кратные 2, два – круглые/

верблюд, если 1/7 его массы равна 100кг / 700кг=7ц/

дельфин — 1/5 — 80кг /400кг=4ц/

тигр — 1/3 — 90кг /270кг /

Из них: 1/8 – занимается легкой атлетикой /24:8=3 чел./

½ — плаванием /24:2=12 чел./

1/6 — танцами /24:6=4 чел./

¼ — музыкой /24:4=6 чел./

Сколько человек занимается л/а, плаванием, танцами, музыкой?

3. Постановка задачи

дроби от числа. /

4. «Открытие» детьми нового знания

• Откройте учебник на стр. 77 задание 1, прочитайте обе задачи.

• Сравните задачи и скажите, чем они похожи? / Одинаковые данные: 12 и ¼ /

• Чем отличаются? / Содержанием и выбором действия при решении /

• Решите задачи 1 и 2. Сделайте вывод.

5. Физкультминутка

• Прочитайте число: 1 359 827 640

• Сколько единиц в разряде десятков миллионов – Хлопните! /5 /

• Сколько единиц в разряде сотен тысяч — Прыгните! / 8 /

• Сколько единиц в разряде единиц миллионов — Присядьте! / 9 /

• Что общего в словах: сложение, вычитание, умножение, деление ?

/Все обозначают действия над числами, средний род, ед. число, окончание — е /

39 : 3 200 x 3 80 : 5

+ 37 — 400 — 4

: 5 : 20 x 5

x 11 + 70 + 40

: 55 — 78 : 50

/2/ /2/ /2/

6. Первичное закрепление

1. Задача 2(а) стр.77 – выполняется коллективно.

   

   

   

   

   

   

   

   

   

   

2. Задача 2(б) стр.77 – в парах.

7. Самостоятельная работа

Задача 3(а) стр.77 – 1 вариант

Задача 3(б) стр.77 – 2 вариант

8. Решение задачи 4 стр. 78 под руководством учителя.

9. Повторение

1. Задание № 7 стр.76. / 1/120, 1% , 1/75, 1/9, 1/5 / — в учебнике.

2. Задание № 9 стр.78 – в тетради.

3. Решение уравнений: № 7 стр.78 (устно)

4. Запишите меры длины в порядке возрастания.

мм см дм м км

10 10 10 1000

/верста, миля, сажень, аршин, сотка, вершок/. Первые единицы длины как в России, так и в других странах были связаны с размерами частей тела человека: сажень, локоть, пядь.

В Англии и США до сих пор используется «ступня» — фут – 31см, «большой палец» — дюйм -25мм и даже «ярд» — 91см – единица длины, появившаяся 900 лет назад.

5. Составьте 4 равенства и объясни геометрический смысл:

a x b = S S : а = b

b x a = S S b = а

6. Решение задач на нахождение периметра, площади у доски (индивидуальная работа).

а = 90м а = 35м а = 30м

в = ? – 1/3 в = 20м , 1/10 от S — овощи S= 960м

P= ?, S= ? S овощей = ? в= ?, Р= ?

7. Решение задачи на смекалку № 12* стр.78.

10. Итог урока

• Чему учились на уроке?

• Как найти дробь от числа?

• Как найти число по дроби?

• Что нового узнали на уроке?

• Как оцениваете свою работу?

Домашнее задание: № 11, № 8 стр.78

Дополнительный материал к уроку: цветные таблицы на развитие логического мышления.

Как делить десятичные дроби на 10, 100, 1000 и т.д?

Для того, чтобы разделить десятичную дробь на 10, 100, 1000, …, надо перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит после единицы в делителе.

При этом иногда приходится сначала написать перед целой частью нуль или несколько нулей.

Например:

374,5 : 100 = 3,745

5,021 : 1000 = 0005,021 : 1000 = 0,005021

0,1 : 100 = 000,1 : 100 = 0,001

В этом онлайн тренажере необходимо выбрать правильный ответ и нажать на него. В случае правильного ответа он загорится зеленым цветом, если ответ неверный — красным. В этом случае попробуйте найти правильный ответ, а затем нажмите кнопку «Дальше».

Онлайн тренажер по математике из раздела «Умножение и деление десятичных дробей»

Закрепляющие файлы для работы.

Менталар желает Вам легкой плодотворной усвояемой работы над собой.

Верьте в себя и у вас все получится!!!

Ваш сайт Менталар.

Сложение смешанных чисел или смешанных дробей.

Сложение смешанных дробей происходит по закону сложения.

У смешанных дробей складываем целые части с целыми и дробные части с дробными.

Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.

Сложим смешанные числа \(3\frac{6}{11}\) и \(1\frac{3}{11}\).

Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.

Выполним сложение смешанных чисел \(7\frac{1}{8}\) и \(2\frac{1}{6}\).

Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь \(7\frac{1}{8}\) на дополнительный множитель 3, а вторую дробь \(2\frac{1}{6}\) на 4.

Вопросы по теме:Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби. В зависимости от типа выражения переходим к алгоритму решения.

Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.

Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.

Пример №1:
Может ли сумма двух правильных дробей в результате получить правильную дробь? Неправильную дробь? Приведите примеры.

Решение:

Дробь \(\frac{5}{7}\) это правильная дробь, она является результатом суммы двух правильных дробей \(\frac{2}{7}\) и \(\frac{3}{7}\).

Дробь \(\frac{58}{45}\) является неправильной дроби, она получилась в результате суммы правильных дробей \(\frac{2}{5}\) и \(\frac{8}{9}\).

Ответ: на оба вопроса ответ да.

Пример №2:
Сложите дроби: а) \(\frac{3}{11} + \frac{5}{11}\)  б) \(\frac{1}{3} + \frac{2}{9}\).

а) \(\frac{3}{11} + \frac{5}{11} = \frac{3 + 5}{11} = \frac{8}{11}\)

б) \(\frac{1}{3} + \frac{2}{9} = \frac{1 \times \color{red} {3}}{3 \times \color{red} {3}} + \frac{2}{9} = \frac{3}{9} + \frac{2}{9} = \frac{5}{9}\)

Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) \(1\frac{9}{47}\)   б) \(5\frac{1}{3}\)

а) \(1\frac{9}{47} = 1 + \frac{9}{47}\)

б) \(5\frac{1}{3} = 5 + \frac{1}{3}\)

Пример №4:
Вычислите сумму: а) \(8\frac{5}{7} + 2\frac{1}{7}\)  б) \(2\frac{9}{13} + \frac{2}{13}\)  в) \(7\frac{2}{5} + 3\frac{4}{15}\)

Решение:

а) \(8\frac{5}{7} + 2\frac{1}{7} = (8 + 2) + (\frac{5}{7} + \frac{1}{7}) = 10 + \frac{6}{7} = 10\frac{6}{7}\)

б) \(2\frac{9}{13} + \frac{2}{13} = 2 + (\frac{9}{13} + \frac{2}{13}) = 2\frac{11}{13} \)

в) \(7\frac{2}{5} + 3\frac{4}{15} = 7\frac{2 \times 3}{5 \times 3} + 3\frac{4}{15} = 7\frac{6}{15} + 3\frac{4}{15} = (7 + 3)+(\frac{6}{15} + \frac{4}{15}) = 10 + \frac{10}{15} = 10\frac{10}{15} = 10\frac{2}{3}\)

Задача №1:
За обедам съели \(\frac{8}{11}\) от торта, а вечером за ужином съели \(\frac{3}{11}\). Как вы думаете торт полностью съели или нет?

Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.

Ответ: весь торт съели.

Режимы счёта

На странице настроек режима можно задавать необходимые параметры генерации примеров с дробями для любого класса.

Онлайн тренажер «Дроби» позволяет генерировать примеры с любыми видами дробей, с любым из четырёх арифметических действий: «сложение – вычитание» или «умножение – деление».

Кнопки на панели настроек работают по принципу «Вкл/Выкл». Если цвет кнопки зелёный — значит в примерах будут использоваться дроби того типа, который описывает кнопка. Если же цвет серый — этот тип дробей использоваться не будет.

В приложении отсутствуют режимы «Уравнение» и «Сравнение» из-за их избыточной сложности. Работа проходит только в режиме «Пример» с возможным использованием следующих типов дробей:

Разные знаменатели — в примере будут появляться обыкновенные дроби с разными знаменателями.

Неправильные дроби — в примере будут появляться обыкновенные неправильные дроби (числитель больше знаменателя).

Смешанные числа — в примере будут появляться смешанные числа (числа, состоящие из целой и дробной частей).

Десятичные дроби — в примере будут появляться дроби в десятичной записи.

Также имеется возможность включить обязательную проверку ответа на сокращение дробной части числа и выделение целой части числа (если имеется). Понять, нужно ли сокращать ответ можно по красному индикатору * на странице настроек и странице ввода ответа.

Все изменения настроек сразу применяются и Вы тут же можете увидеть как будет выглядеть новый пример в графе «Например». Когда подбор нужных характеристик окончен, нажмите на кнопку ПОЕХАЛИ.

Процесс счёта

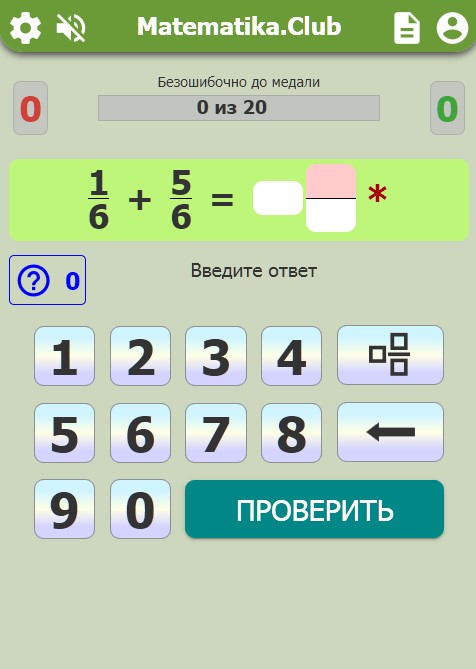
Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звуковые уведомления или перейти к Подробному решению текущего примера.

Вы решаете заданый пример, вводите ответ по частям (целое, числитель, знаменатель) в соответствующие поля с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки ответа Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.

Количество правильных, неправильных ответов и число подсказок можно увидеть в соответствующих индикаторах.

Подробное решение примеров

В любой момент работы с тренажером вы можете перейти в разделу «Подробного решения примера», если обычной подсказки в виде верного ответа вам не достаточно. Для этого кликните на соответствующую иконку сверху, либо перелестнув страницу вниз.

Здесь вы сможете посмотреть подробное решение примера с дробями со всеми преобразованиями, сокращениями и упрощениями.

Дополнительная информация

Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:

домен сайта + раздел приложения + кодировка данного режима

например: matematika.club/drobi/#60101

Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.

Три вида задач на дроби

Задачи на дроби бывают следующих видов:

1. На отыскание указанной части (дроби) данного числа;
2. На отыскание числа, если известна часть (дробь) этого числа;
3. На отыскание части (дроби), которую составляет одно число от другого.

Задачи на дроби удобно решать следующим образом.

1. Делается рисунок. На этом рисунке:

а) отмечается произвольный отрезок прямой, который изображает «целое» – отрезок, длина которого известна или является искомой величиной по условию задачи;б) приблизительно отмечается известная или неизвестная часть этого целого;в) над отрезком и над частью указываются известные или неизвестные величины, которые они изображают; под ними – соответствующие им известные или неизвестные дроби.

2. Находится, чему равна одна часть целого.

3. Находится искомая величина, записывается ответ.

Пример 1.

Найдём 3/8 от 72 метров.

Решение.

Решаем задачу, используя указанный алгоритм.

Выполним чертёж к задаче: сначала изобразим произвольный отрезок. Пусть его длина будет якобы равна 72 м. Нам необходимо найти длину 3/8 этого отрезка. Отметим на данном отрезке отрезок, приблизительно равный 3/8 от 72 м. Длина этого отрезка неизвестна: обозначим его буквой  m.

Далее найдём, чему равна одна восьмая часть целого. Каждая из 8 равных частей данного отрезка будет равна 72 : 8 = 9. Другими словами, 1/8 числа 72 – это 72 : 8 = 9.

Теперь мы можем найти искомую величину:

3/8 от 72 – это (72 : · 3 = 27.

Ответ: 27 м.

Пример 2.

Найдём число, если 11/7 этого числа равны 77.

Решение.

Изобразим произвольный отрезок. Будем считать, что его длина соответствует неизвестному числу k.

В условии задачи говорится об известном числе 77, которое составляет 11/7 неизвестного числа k. Чтобы изобразить его на рисунке, необходимо разделить отрезок k на 7 равных частей и отложить 11 таких частей.

Далее найдём, чему равна одна часть целого. Для этого воспользуемся тем, что 11/7 числа составляют 77. Каждая из 11 равных частей, на которые разделён отрезок, имеет длину 77 : 11 = 7. Теперь мы можем найти искомую величину:

k = (77 : 11) · 7 = 49.

Ответ: 49.

Пример 3.

Купили провод длиной 23 метра. Израсходовали 20 метров. Какая часть купленного провода израсходована?

Решение.

Начертим отрезок, изображающий длину купленного провода. Отметим на отрезке длину израсходованного провода.

Если мысленно разделить отрезок длиной 23 метра на отдельные метры, то каждая такая часть составляет 1/23 часть всего провода: 23 м составляют 23/23, 20 метров составляют 20/23.

Ответ: 20 м = 20/23 от 23 метров.

Остались вопросы? Не знаете, как решить задачу?Чтобы получить помощь репетитора – зарегистрируйтесь.

blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Сложение дробей

Самый простой вариант, когда дроби, которые надо сложить, имеют одинаковый знаменатель. 

Ты же еще не забыл, что это такое, правда?

Например, \( \displaystyle  2/5+1/5\). Вспомнив пример с кусочками пирога, думаю, ты без проблем догадаешься, что если складывать равные дольки одного пирога, то знаменатель меняться не будет, а складываются лишь числители.

Сложение будет выглядеть следующим образом: \( \displaystyle  \frac{2}{5}+\frac{1}{5}=\frac{2+1}{5}=\frac{3}{5}\). Не сложно догадаться и как складывать смешанные дроби.

Отдельно складываются целые и дробные части:

\( \displaystyle  2\frac{2}{3}+4\frac{1}{3}=6\frac{2+1}{3}=6\frac{3}{3}=7\).

А что, если знаменатели у дробей разные, а? Например, \( \displaystyle  2/3+1/2\).

И тут ты сразу вспоминаешь, что мы проходили приведение дробей к общему знаменателю, и, наконец, становится понятно, зачем это было учить!

В данном примере общим знаменателем будет число \( \displaystyle  6\), как наименьшее общее кратное чисел \( \displaystyle  2\) и \( \displaystyle  3\). \( \displaystyle  \frac{2}{3}+\frac{1}{2}=\frac{4}{6}+\frac{3}{6}=\frac{7}{6}=1\frac{1}{6}\).

Поскольку ты теперь умеешь приводить неправильную дробь к смешанной дроби, то открою тебе секрет, что это является не просто хорошим тоном, но и обязательным действием при упрощении выражений, после получения ответа избавиться от неправильных дробей.

С десятичными дробями все еще проще. 

Сложение делается, как и с обычными числами, только не забывай про запятую. Вот тебе пример: \(\displaystyle15,2+2,91\).

Я предлагаю решать так: удобнее всего вычитать в столбик, расположив одну дробь под другой, но при этом запятая должна стоять строго под запятой вне зависимости от количества знаков до и после нее.

Как ты видишь, у второй дроби после запятой было на один знак больше. Для достижения одинакового количества знаков, я добавил еще один ноль в конце первой дроби.

Прогресс и достижения

Приложение также предусматривает небольшой соревновательный момент через получение медалей за безошибочность — правильное решение N примеров подряд.

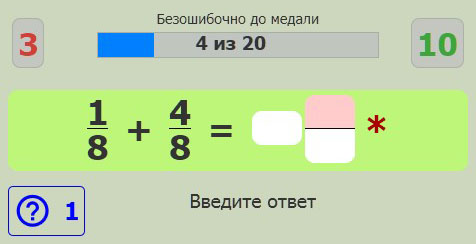
Если во время решения была использована подсказка, то верный ответ не идет в зачет прогресса. Ошибка же сразу обнуляется весь прогресс. Поэтому будьте максимально осторожны, если хотите получить медаль — один неверный шаг и придется начинать все с начала.

Узнать, получили ли Вы уже медаль за конкретный режим можно на странице «Статистика» в профиле или в самом приложении.

Такой интерфейс делает процесс решения математических примеров более интересным, являясь также простой мотивацией для детей.

Приведение дробей к общему знаменателю

Представляешь, любые две дроби можно привести к общему знаменателю! Ну, если тебя это не поразило, ты, наверное, не понял о чем я. Вот смотри. Есть две дроби \( \displaystyle  1/3\) и \( \displaystyle  3/5\).

Тебе надо изменить эти дроби так, чтоб значение дробей не поменялось, но в знаменателе у обеих стало одно и то же число. Подскажу лишь, что для этого нужно воспользоваться основным свойством дроби.

Ладно, так и быть, покажу сам: \( \displaystyle  1/3=5/15\); \( \displaystyle  3/5=9/15\). Как ты видишь в знаменателе у обеих дробей \( \displaystyle  15\), и при этом, если сократить дроби, первую на \( \displaystyle  5\), а вторую на \( \displaystyle  3\), то получатся те же \( \displaystyle  1/3\) и \( \displaystyle  3/5\)!

Сказать, как это делается? Так и быть, тебе сегодня везет, читай ниже.

дробей в четвертом: как научить складывать и вычитать

Купить сейчас

Купить сейчас

Купить сейчас

Купить сейчас

15 февраля 2021 г. Оставить комментарий

Четвертый класс действительно фокусируется на закреплении идеи о том, что дроби — это части целого, которые можно складывать или разбивать. Учащиеся работают исключительно с одинаковыми знаменателями до 9.0021 складывать, вычитать, моделировать, писать уравнения и обосновывать свое мышление . Учащиеся должны уметь делать это со смешанными числами и дробями, а также использовать визуальные средства для решения текстовых задач. Как мне выполнить все, что вы спрашиваете?

Сложение дробей с одинаковыми знаменателями

Шаблоны и числовые ряды идеально подходят для четвероклассников, поскольку они обеспечивают согласованные знаменатели.

При использовании шаблонов учащиеся могут заменять дробные имена фигурами.

1 ромб + 2 ромба = 3 ромба. 1 треть + 2 трети = 3 трети.

Числовые ряды тоже хороши, и ничего страшного, если учащиеся не будут точны при делении своих числовых рядов. Сетчатая бумага поможет сохранить их работу аккуратной, но это не обязательно. В этом примере вы можете увидеть, как числовые линии также могут показать, как в сумме дроби могут составлять более одного целого.

Вычитание дробей с одинаковыми знаменателями

Не используйте эти шаблоны для вычитания дробей. Учащиеся, которым сложно, оценят возможность использовать кубики шаблона для построения дроби, а затем вынимать часть за частью, чтобы вычесть и посмотреть, что осталось. Здесь мы начинаем с 5/6 и вычитаем 3/6, чтобы показать, что осталось 2/6.

Некоторым учащимся также будет полезен обратный отсчет по числовой строке , чтобы показать, как вычитать. Когда вы начинаете с 1 1/3 и вам нужно вычесть 2/3, некоторые ученики застрянут, так как у них нет 2/3 для вычитания. При использовании числовой строки они могут отсчитывать 1/3 за раз, чтобы показать, что осталось 2/3.

Решайте текстовые задачи на профессиональном уровне

Ключ к решению текстовых задач заключается в том, чтобы убедиться, что вы действительно понимаете, о чем идет речь. Если учащийся не может объяснить задачу, не глядя на нее, он, вероятно, не понимает ее достаточно хорошо, чтобы решить ее… пока. Перечитывание проблемы и рисование картинки — бесценные инструменты для достижения успеха.

Вот пример того, как вы можете помочь своим учащимся понять дроби с помощью текстовых задач. Ожидается, что студенты моделируют и объясняют свое мышление .

Занятия по математике для 3-го класса: распечатка и цифровая математика

Получите доступ к ТРЕМ печатным и цифровым математическим играм для повторения дробей!

Я хочу эту халяву!

Вам также могут понравиться эти посты

Получите мгновенный доступ ко всем ресурсам Math Tech Connections!

Вступай в Клуб!

Привет, друзья!

Меня зовут Мариэла! Я преподаватель и основатель Math Tech Connections. Я начал создавать ресурсы для своих учеников, когда увидел, что обучение по учебнику не работает. Студентам нужны увлекательные, практические занятия! Моя цель — сэкономить ваше время с помощью качественных, соответствующих стандартам ресурсов, которые делают математику увлекательной.

Оставайтесь на связи!

Управление согласием

Распространенные ошибки и на что следует обратить внимание. Тренажер

Давайте возьмем пример, сложив вместе ¾ и ⅙.

Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.

Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.

Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.

Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.

Другие распространенные ошибки включают:

Оставляйте знаменатель неизменным во время вопросов, касающихся умножения или сложения.

Десятичные дроби

Существует еще один вид дробей, уверен ты его знаешь. Бери калькулятор и дели \( \displaystyle  11\) на \( \displaystyle  2\), например. Что пишет, \( \displaystyle  5,5\)? Что за штука такая?

Читается это как пять целых и пять десятых, равносильно \(\displaystyle5\frac{5}{10}\). Иными словами \( \displaystyle  11/2=5,5=5\frac{5}{10}\), все это одно и то же.

Дроби типа \( \displaystyle  5,5;\text{ }42,02;\text{ }0,122\) – все это десятичные дроби – это те же самые обыкновенные дроби, но в так называемой десятичной записи.

Десятичная запись используется для дробей со знаменателями \( \displaystyle  10\), \( \displaystyle  100\), \( \displaystyle  1000\) и т. д. В десятичных дробях так же есть целая и дробная части.

Для ясности возьмем вот такую дробь \( \displaystyle  12,856\):

• до запятой – целая часть (\( \displaystyle  12\));
• первый знак после запятой – десятые доли (\( \displaystyle  8/10\));
• второй – сотые доли (\( \displaystyle  5/100\));
• третий – (\( \displaystyle  6/1000\)).