Четные и нечетные числа для дошкольников

Четность чисел — Сайт rmomatematik!

·        
Четные числа — это те, которые делятся на 2 без остатка (например, 2, 4, 6 и т.п.). Каждое такое число можно записать в виде 2K,
подобрав подходящее целое K (например, 4 = 2 х 2, 6 = 2 х 3, и т.д.).

·        
Нечетные числа — это те, которые при делении на 2 дают в остатке 1 (например, 1, 3, 5 и т.п.). Каждое такое число можно записать в виде 2K + 1, подобрав подходящее целое K (например, 3 = 2 х 1 +
1, 5 = 2 х 2 + 1, и т.д.).

Сложение и вычитание:

• • Чётное ± Чётное = Чётное
  • Чётное ± Нечётное = Нечётное
  • Нечётное ± Чётное = Нечётное
  • Нечётное ± Нечётное = Чётное
• Умножение:
• • Чётное × Чётное = Чётное
  • Чётное × Нечётное = Чётное
  • Нечётное × Нечётное = Нечётное
• Деление:
• • Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат целое число,
    то оно может быть как чётным, так и нечётным)
  • Чётное / Нечётное -­— если результат целое число,
    то оно Чётное
  • Нечётное / Чётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
  • Нечётное / Нечётное —если результат целое число,
    то оно Нечётное

  
       Сумма любого числа четных чисел –
четно.

          Сумма нечетного
числа нечетных чисел – нечетно.

          Сумма четного
числа нечетных чисел – четно.

          Разность двух
чисел имеет ту же четность, что и их сумма.(напр. 2+3=5 и 2-3=-1 оба нечетные)

          Алгебраическая (со знаками + или -) сумма целых чисел имеет ту же четность, что и их сумма.(напр. 2-7+(-4)-(-3)=-6 и 2+7+(-4)+(-3)=2 оба четны)

        Идея
четности имеет много разных применений. Самые простые из них:

1. Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их четное число (и каждого вида поровну).

2. Если в некоторой цепочке чередуются объекты двух видов, а начало и конец цепочки разных видов, то в ней четное число объектов,
если начало и конец одного вида, то нечетное число. (четное число объектов соответствует нечетному числу
переходов между ними и наоборот !!!)

2′. Если у объекта чередуются два возможных состояния, а исходное и конечное состояния различны, то периодов пребывания объекта в том или ином состоянии — четное число, если исходное и конечное состояния совпадают — то нечетное.
(переформулировка п.2)

3. Обратно: по четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.

3′. Обратно: по числу периодов пребывания объекта в одном из двух возможных чередующихся состояний можно узнать, совпадает ли
начальное состояние с конечным. (переформулировка п.3)

4. Если предметы можно разбить на пары, то их количество четно.

5. Если нечетное число предметов почему-то удалось разбить на пары, то какой-то из них будет парой к самому себе, причем такой
предмет может быть не один (но их всегда нечетное число).

(!) Все эти соображения можно на олимпиаде
вставлять в текст решения задачи, как очевидные утверждения.

Примеры:

Задача 1. На плоскости
расположено 9 шестеренок, соединенных по цепочке (первая со второй, вторая с третьей … 9-я с первой). Могут ли они вращаться одновременно?

Решение: Нет, не могут. Если бы
они могли вращаться, то в замкнутой цепочке чередовалось бы два вида шестеренок: вращающиеся по часовой стрелке и против часовой стрелки (для решения задачи не имеет никакого значения, в каком именно направлении вращается первая шестеренка !) Тогда  всего должно быть
четное число шестеренок, а их 9 штук?! ч.и.т.д. (знак «?!» обозначает получение противоречия)

Задача 2. В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки + и -, чтобы
получилось выражение, равное нулю?Решение: Нет, нельзя. Четность
полученного выражения всегда будет совпадать с четностью суммы 1+2+…+10=55, т.е. сумма всегда будет нечетной. А 0
— четное число?! ч.т.д.

Общие сведения

Определения терминов в математике занимают первое место, поскольку только формулировки дают понять основную суть какого-либо компонента. Следует отметить, что числа (значения) и цифры существенно отличаются между собой, как по логике, так и по сфере применения.

Чтобы понять основную суть значений и цифр, необходимо ознакомиться с их определениями. Число — некоторая математическая количественная характеристика, обозначающая конкретное значение. Цифра — математический элемент (символ), используемый для формирования численных величин. Он не является количественной характеристикой.

Иными словами, четные компоненты образуют соответствующее множество, а именно: {0,2,4,6,8}. Если конвертированную цифру невозможно разделить на два без остатка, то значит она является нечетной.

Графы

Мы определим граф как набор точек (вершин), некоторые из которых соединены между собой линиями (ребрами). Количество ребер, выходящих из данной вершины, мы будем называть ее степенью. Вершина графа, имеющая нечетную степень, называется нечетной, а имеющая четную степень — четной.

Теорема. Число нечетных вершин любого графа — четно.

Задачи

2.1. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля — Меркурий, Плутон — Венера, Земля — Плутон, Плутон — Меркурий, Меркурий — Венера, Уран — Нептун, Нептун — Сатурн, Сатурн — Юпитер, Юпитер — Марс и Марс — Уран. Можно ли добраться с Земли до Марса?

2.2. В Солнечном городе есть 9 домов с номерами 1, 2, 3, 4, 5, 6, 7, 8, 9. Незнайка обнаружил, что два дома соединены дорогой в том и только том случае, если двузначное число, составленное из номеров этих домов, делится на 3, и никакие 2 дороги не пересекаются. Можно ли добраться из дома № 1 в дом № 9?

2.3. Доска имеет форму креста, который получается, если из квадратной доски 4 × 4 выкинуть угловые клетки. Можно ли обойти ее ходом шахматного коня и вернуться на исходное поле, побывав на всех полях ровно по одному разу?

2.4. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?

2.5. В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 — по 4 друга, а 10 — по 5 друзей?

2.6. В городе Маленьком все еще 15 телефонов. Можно ли их соединить проводами так, чтобы было 4 телефона, каждый из которых соединен с тремя другими, 8 телефонов, каждый из которых соединен с шестью, и 3 телефона, каждый из которых соединен с пятью другими?

2.7. У короля 19 баронов-вассалов. Может ли оказаться так, что у каждого вассального баронства 1, 5 или 9 соседних баронств?

2.8. Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог?

2.9. Джон, приехав из Диснейленда, рассказывал, что там на заколдованном озере имеются 7 островов, с каждого из которых ведет 1, 3 или 5 мостов. Верно ли, что хотя бы один из этих мостов выходит на берег озера?

2.10. Докажите, что число людей, когда-либо живших на Земле и сделавших нечетное число рукопожатий, четно.

2.11. Можно ли на плоскости нарисовать 9 отрезков так, чтобы каждый пересекался ровно с тремя другими?

Сумма, произведение, частное четных (нечетных) чисел

Утверждение 1. Сумма двух четных чисел — четное число.

Доказательство. Пусть числа m и n являются четными. Докажем, что число r = m + n также четно. m=2k, n=2p, где k и p — целые числа. Тогда r = m + n = 2k + 2p = 2(k + p) = 2s. Если числа k и p являются целыми, то их сумма s — тоже целое число. Мы доказали, что число r может быть представлено в виде произведения двойки и целого числа. Доказательство завершено.

Утверждение 2. Сумма двух нечетных чисел — четное число. Докажите самостоятельно.

Утверждение 3. Сумма четного и нечетного чисел — нечетное число. Докажите самостоятельно.

Утверждение 4. Произведение двух нечетных чисел — нечетное число.

Доказательство. Пусть числа m и n являются нечетными. Докажем, что число r = m • n также нечетно.
m = 2k + 1, n = 2p + 1, где k и p — целые числа.
Тогда r = m • n = (2k+1) • (2p+1) = 4kp + 2k + 2p + 1 = 2(2kp + k + p) + 1 = 2s + 1.
Если числа k и p являются целыми, то число s = 2kp + k + p — тоже целое число.
Мы доказали, что число r может быть представлено в виде r = 2s + 1, следовательно, является нечетным. Ч. т. д.

Утверждение 5. Произведение двух четных чисел — четное число. Докажите самостоятельно.

Утверждение 6. Произведение четного и нечетного чисел — четное число. Докажите самостоятельно.

А если мы поделим четное число на четное (не равное нулю)? Что получим: чет или нечет? Естественно, однозначного ответа дать нельзя. Например, при делении 12 на 4 мы получаем нечетный результат, а при делении 32 на 4 — четный.

Если вы уже заскучали, переходите ко 2-й части статьи. Потом всегда сможете вернуться. Если же все эти теоретические построения вас не слишком утомили, давайте продолжим.

А почему, собственно, мы рассматриваем только два числа. Давайте мыслить шире!

Утверждение 7. Сумма любого количества четных чисел четна.

Доказательство. Пусть числа M₁, M₂, …, M_N являются четными, тогда их можно представить в виде 2K₁, 2K₂, … , 2K_N, где K₁, K₂, …, K_N — целые числа.
Тогда: M₁ + M₂ + … + M_N = 2K₁ + 2K₂ + … + 2K_N = 2( K₁ + K₂ + … + K_N) = 2S, где S-целое число. Четность доказана.

Утверждение 8. Сумма четного количества нечетных чисел четна. Сумма нечетного количества нечетных чисел нечетна. Докажите самостоятельно.

Утверждение 9. Произведение может быть нечетным только в том случае, если все сомножители нечетны. Докажите самостоятельно.

Так, сумма 2+4+6+…+1022+1024 четна, поскольку все слагаемые четны. Сумма 1+3+5+7+9 нечетна, т. к. содержит 5 нечетных слагаемых. Произведение 2*3*4*…*1001*1002 четно уже хотя бы по той причине, что первый сомножитель является четным.

Задание 4. Четными или нечетными будут следующие выражения: а) 2+12+22+…+1002+1012+1022, б) 1+11+111+…+111111+1111111, в) 3*13*23*…*10003*10013*10023, г) 2*3*4*…*12357891 ?

Задание 5. Докажите, что произведение всех простых чисел, не превосходящих 1000000, четно. Докажите, что произведение любого количества простых чисел, каждое из которых больше 100, нечетно. Напомню, что натуральное число называется простым, если делится только на себя и на 1.

Чётные числа

Общеизвестно, что чётные числа
— те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.

А что означают чётные числа
относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.

У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».

А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.

Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?

Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.

Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.

История и культура [ править | править код ]

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь», а нечётные — «ян» .

В разных странах существуют связанные с количеством даримых цветов традиции. Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье. В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.

Как наглядно представить четные и нечетные числа?

Задача объяснить ребенку понятия «четные» и «нечетные» числа может быть вызовом для многих родителей. Давайте рассмотрим игру, которая поможет вашему ребенку лучше понять эти понятия.

Возьмите большой лист бумаги и нарисуйте на нем несколько кружков. Пусть каждый кружок представляет собой число. Теперь объясните своему ребенку, что если число делится на 2 без остатка, то оно является четным числом.

Например, если вы нарисовали 6 кружков и сказали ребенку, что это представляет число 6, то можно продемонстрировать, что это число делится на 2 без остатка, поскольку его можно разделить на две группы по 3 кружка в каждой.

Теперь рассмотрим нечетное число. Если число не делится на 2 без остатка, то оно является нечетным числом. Например, если нарисовать 7 кружков и сказать, что это число 7, то невозможно разделить эти кружки на две равные группы, так как останется один кружок без пары.

Игра с кружками поможет ребенку визуально представить понятия «четные» и «нечетные» числа. Она позволит ему лучше понять, что число, которое делится ровно на 2, является четным, а число, которое не делится на 2 без остатка, является нечетным. Таким образом, ваш ребенок сможет легко запомнить и различать эти понятия в математике.

Зрительная аналогия для четных чисел

Задача родителя объяснить понятие четного числа ребенку может быть сложной, особенно если он только начинает учить математику. Для того чтобы сделать объяснение более понятным и интересным, можно использовать зрительную аналогию.

Представьте, что мы играем в игру. У нас есть несколько ребят, и мы хотим их разделить на две команды. И чтобы это было честно, мы хотим, чтобы в каждой команде было одинаковое число ребят. Но как это сделать, если у нас нечетное число ребят?

Здесь на помощь приходят четные числа. Четное число можно представить себе в виде двух одинаковых групп. Если у нас, например, 6 ребят, мы можем сделать две команды по 3 ребят в каждой. В каждой команде будет одинаковое и справедливое количество участников.

Таким образом, четное число можно представить как две равные части, которые можно поделить между разными группами или командами.

Используя эту зрительную аналогию, вы можете объяснить понятие четных чисел ребенку и сделать учение математике интересным и игровым процессом.

3 ребят	3 ребят
1 команда	2 команда

Зрительная аналогия для нечетных чисел

Ребенку иногда сложно понять математические понятия, такие как «четное» и «нечетное». Чтобы объяснить ребенку нечетные числа, мы можем использовать зрительную аналогию.

Давай представим, что у тебя есть задача. Ты должен разделить своих игрушки поровну между собой и своим другом. Если у тебя четное количество игрушек, то они разделятся поровну, и каждому из вас достанется одинаковое количество игрушек.

Игрушки	Твои	Друга
2	1	1
4	2	2
6	3	3

Теперь, давай представим, что у тебя нечетное количество игрушек. Как ты думаешь, будут ли они делиться поровну?

Когда у тебя нечетное количество игрушек, их нельзя разделить поровну между тобой и твоим другом. Одна игрушка останется без пары.

Игрушки	Твои	Друга
1	1
3	2	1
5	3	2

Таким образом, нечетные числа имеют остаток, который не может быть разделен поровну. Эта зрительная аналогия поможет ребенку лучше понять понятие нечетных чисел.

Четность

Все знают, что числа бывают четные и нечетные. Четные числа — это те, которые делятся на 2 без остатка (например, 2, 4, 6 и т. п.). Каждое такое число можно записать в виде 2k, подобрав подходящее целое k (например, 4 = 2 × 2, 6 = 2 × 3, и т. д.). Нечетные числа — это те, которые при делении на 2 дают в остатке 1 (например, 1, 3, 5 и т. п.). Каждое такое число можно записать в виде 2k + 1, подобрав целое подходящее k (например, 3 = 2 × 1 + 1, 5 = 2 × 2 + 1, и т. д.).

Четные и нечетные числа обладают замечательными свойствами:

а) сумма двух четных чисел четна;

б) сумма двух нечетных чисел четна;

в) сумма четного и нечетного чисел — нечетное число.

Задачи

1.1. Докажите приведенные выше свойства а) — в).

1.2. Какой (четной или нечетной) будет сумма нескольких

а) четных чисел;

б) нечетных чисел?

1.3. Докажите, что

а) произведение двух четных чисел четно;

б) произведение двух нечетных нечетно;

в) произведение четного и нечетного чисел — четное число.

1.4. Каким (четным или нечетным) будет произведение нескольких

а) четных чисел;

б) нечетных чисел?

1.5. Придумайте четыре целых числа, сумма и произведение которых являются нечетными числами.

1.6. Гости на дне рождения великого русского художника Валентина Серова сидели за круглым столом и ели персики. Когда персики закончились, гости посчитали персиковые косточки, и оказалось, что у каждой пары сидящих рядом гостей количество косточек отличалось на 1. Могло ли за столом сидеть а) 3; б) 4; в) 98; г) 99 гостей?

1.7. В карманных часах Наполеона было 7 шестеренок, соединенных по цепочке (см. рис.). Кутузов, посмотрев на это, сказал, что они не могут вращаться одновременно. Прав ли великий русский полководец?

1.8. Петька купил журнал «Работа & Зарплата» объемом 136 листов со страницами, пронумерованными по порядку числами от 1 до 272. Василий Иванович вырвал из этого журнала 25 листов и сложил все 50 номеров страниц. Могло ли у него получиться 1990?

1.9. В дружине Дядьки Черномора 100 богатырей, и каждый вечер трое из них идут за пивом. Может ли через некоторое время оказаться так, что каждый с каждым ходил за пивом ровно один раз?

1.10. 25 гусар и 25 воспитанниц пансиона благородных девиц сидят за круглым столом. Докажите, что у кого-то из сидящих за столом оба соседа — гусары.

1.11. Улитка ползет по плоскости с постоянной скоростью, каждые 15 минут поворачивая под прямым углом. Докажите, что вернуться в исходную точку она сможет лишь через целое число часов.

1.12. Три черепахи играют на прямой в чехарду. Каждый раз одна из них прыгает через другую (но не через двух сразу!). Могут ли они после 1991 прыжка оказаться на прежних местах?

1.13. В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки «+» и «-» так, чтобы значение полученного выражения было равно нулю?

1.14. Дан осесимметричный выпуклый 101-угольник. Докажите, что ось симметрий проходит через одну из его вершин. Что можно сказать в случае 10-угольника?

1.15. В парламенте страны Зям-Лям две палаты, имеющие равное число депулямов

В голосовании по важному вопросу приняли участие все депулямы, причем воздержавшихся не было. Когда председатель сообщил, что решение принято с преимуществом в 23 голоса, лидер оппозиции заявил, что результаты голосования сфальсифицированы

Как он это понял?

1.16. На доске написаны числа 0, 1, 0, 0. За один шаг разрешается прибавить 1 к любым двум из них. Можно ли, повторяя эту операцию, добиться, чтобы все числа стали равными?

Что такое четные и нечетные числа?

Прежде чем приступать к знакомству с четными и нечетными числами, следует убедиться в том, что малыш хорошо знает последовательность цифр. Используйте для проверки игровой формат «Мои и твои цифры». У игры очень простые правила: вы называете цифру 1, ребёнок называет следующую. Затем снова ваша очередь (цифра 3), а потом очередь ребенка (цифра 4) и так далее до десяти или до двадцати. На следующем этапе можно поменять последовательность: числовой ряд начинает ребенок, а вы его продолжаете. Это хорошая тренировка для памяти и внимательности.

Теперь можно объяснить ребёнку, что такое чётные и нечётные числа. Итак, четные числа – это те, которые делятся на два без остатка. Нечетные разделить пополам нельзя. Малышу будет проще понять этот принцип на наглядном примере:

Возьмём три апельсина и попробуем разделить их поровну между тобой и другом. Как это сделать и сколько апельсинов достанется каждому из вас?

Наверняка ребёнок придёт к выводу, что разделить фрукты ровно пополам не получится. Кому-то достанется больше, а кому-то – меньше. Или же один апельсин придётся разрезать, то есть каждому достанется по одному целому фрукту и ещё по половинке.

А если вам дали четыре апельсина? Вы с другом сможете поделить их поровну?

В этом случае ребенок разделит витаминный запас так, чтобы никому не было обидно: каждому достанется по два апельсина.

Также следует объяснить ребенку, что четные и нечетные числа в последовательном ряду чередуются друг с другом:

, 1, 2, 3, 4, 5, 6, 7, 8, 9.

И ещё несколько правил, которые необходимо запомнить:

Все числа, оканчивающиеся на 0, 2, 4, 6, 8, являются четными.

Числа, оканчивающиеся на 1, 3, 5, 7, 9 – нечетные.

Эти правила применяются как к простым однозначным числам, так и к двузначным. Понимание сути поможет ребенку в дальнейшем справляться со сложными математическими задачами.

Графы

Мы определим граф как набор точек (вершин), некоторые из которых соединены между собой линиями (ребрами). Количество ребер, выходящих из данной вершины, мы будем называть ее степенью. Вершина графа, имеющая нечетную степень, называется нечетной, а имеющая четную степень — четной.

Теорема. Число нечетных вершин любого графа — четно.

Задачи

2.1. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля — Меркурий, Плутон — Венера, Земля — Плутон, Плутон — Меркурий, Меркурий — Венера, Уран — Нептун, Нептун — Сатурн, Сатурн — Юпитер, Юпитер — Марс и Марс — Уран. Можно ли добраться с Земли до Марса?

2.2. В Солнечном городе есть 9 домов с номерами 1, 2, 3, 4, 5, 6, 7, 8, 9. Незнайка обнаружил, что два дома соединены дорогой в том и только том случае, если двузначное число, составленное из номеров этих домов, делится на 3, и никакие 2 дороги не пересекаются. Можно ли добраться из дома № 1 в дом № 9?

2.3. Доска имеет форму креста, который получается, если из квадратной доски 4 × 4 выкинуть угловые клетки. Можно ли обойти ее ходом шахматного коня и вернуться на исходное поле, побывав на всех полях ровно по одному разу?

2.4. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?

2.5. В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 — по 4 друга, а 10 — по 5 друзей?

2.6. В городе Маленьком все еще 15 телефонов. Можно ли их соединить проводами так, чтобы было 4 телефона, каждый из которых соединен с тремя другими, 8 телефонов, каждый из которых соединен с шестью, и 3 телефона, каждый из которых соединен с пятью другими?

2.7. У короля 19 баронов-вассалов. Может ли оказаться так, что у каждого вассального баронства 1, 5 или 9 соседних баронств?

2.8. Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог?

2.9. Джон, приехав из Диснейленда, рассказывал, что там на заколдованном озере имеются 7 островов, с каждого из которых ведет 1, 3 или 5 мостов. Верно ли, что хотя бы один из этих мостов выходит на берег озера?

2.10. Докажите, что число людей, когда-либо живших на Земле и сделавших нечетное число рукопожатий, четно.

2.11. Можно ли на плоскости нарисовать 9 отрезков так, чтобы каждый пересекался ровно с тремя другими?

“Четные и нечетные числа”

Урок 3 7. Четные и нечетные числа

Цели: познакомить с понятиями четные и нечетные числа; повторить табличные случаи умножения и деления на 2 до 20; совершенствовать умение решать задачи.

Планируемые результаты: учащиеся научатся определять четные и нечетные числа; осуществлять подведение под понятие на основе распознавания объектов, выделения существенных признаков и синтеза; проводить сравнение, классификацию по заданным критериям; принимать и сохранять учебную задачу; учитывать установленные правила в планировании и контроле способа решения; владеть диалогической формой коммуникации; контролировать действия партнера.

Ход урока

1. Организационный момент

Звонок прозвенел —

Он позвал на урок.

Пора! Тишина!

К нам наука идет!

1. Актуализация знаний

2. Игра кленовые листья. (На каждый ряд дается кленовый листок, на котором написаны примеры. Ребята решают их. Побеждает тот ряд, который решил быстрее и не допустил ошибок)

1. Математический диктант

Взаимопроверка

1. Какое число нужно разделить на 6, чтобы получилось 2? (12.)

2. 2.На сколько 18 меньше, чем 32? (На 14.)

3. Найдите частное чисел 14 и 7. (2.)

4. Я задумала число, умножила его на 10 и получила 20. Какое число я задумала? (2.)

5. Уменьшите 10 в 2 раза.

   (5.)

6. Умножьте произведение чисел 2 и 3 на 2. (12.)

7. Из какого числа вычли 15 и получили 15? (30.)

8. Какое двузначное число в таблице умножения на 2 оканчивается цифрой 6. (16.)

9. 9) На сколько нужно умножить 4, чтобы получилось 8? (На 2.)

10. Сколько прибавили к произведению чисел 3 и 6, если получили 20? (2.)

11. На сколько нужно умножить 2, чтобы получилось 18? (На 9.)

12. Сколько вычли из произведения чисел 5 и 20, если получили 30? (70.)

(Взаимопроверка по образцу. Взаимооценка с помощью знаков «!»,«+»,«—».)

Самоопределение к деятельности

(Учитель записывает на доске числа от 1 до 10 в ряд через запятую.)

Какие из этих чисел делятся на 2? (2, 4, 6, 8и 10.)

Те числа, которые делятся на 2, называются четными, а те, которые не делятся на 2, называются нечетными.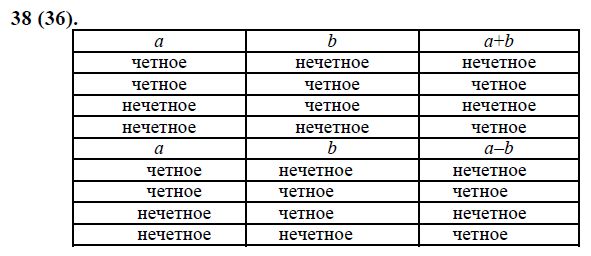

(Учитель подчеркивает четные числа.)

• Назовите все нечетные числа от 1 до 10. (I, 3, 5, 7и 9.) (Учитель записывает на доске числа от 11 до 20.)

• Какие из этих чисел делятся на 2?

• Какие числа не делятся на 2?

(Сформулируйте задачи урока. (Узнать, какие числа называются четными и нечетными, учиться их определять.)

1. Работа по теме урока

Числа которые делятся на 2, называют четными.

Числа которые не делятся на 2 нечетные.

• Сделайте вывод: почему число 10 четное?

• Почему число 7 нечетное?

№1

В «Юнионе» 23 октября стоится премьера сказки «Конек горбунок». Начало сеанса в 11 часов. Продолжительность 2 часа. Путь от дома до «Юниона» занимает 20 минут. В какое время надо выти из дома чтобы успеть за 10 минут до начала.

№2

Мама вам дала 100 руб на покупку молока, хлеба и сметаны. Хватит ли денег, если молоко стоит 35 руб, хлеб 34 руб, сметана 38? Хватит ли денег на покупку?

1. Физкультминутка

А теперь, ребята, встали.

Быстро руки вверх подняли,

В стороны, вперед, назад.

Повернулись вправо, влево.

Тихо сели, вновь за дело.

Учебник стр 45 №4

Выполни вычисления. Подчеркни значения выражений, которые являются четными числами.

9-2        3-2        14:2        18:9

2-6        8-2        20:2        8:4

(Самопроверка по образцу.)

1. Подведение итогов урока

• Какие знания вы сегодня получили?

• Что интересного случилось на уроке?

Домашнее задание

Учебник:

Способы получения нечетных и четных цифр

Для получения четных и нечетных цифр от 1 до 1000 через запятую можно использовать различные способы. Вот несколько из них:

1. Использовать цикл для перебора всех чисел от 1 до 1000 и проверки их на четность или нечетность. Четные числа можно сохранить в отдельную переменную или массив и затем вывести их через запятую. Аналогично можно поступить с нечетными числами.
2. Разделить все числа от 1 до 1000 на две группы: четные и нечетные. Для этого можно использовать операцию деления по модулю на 2. Если результат операции равен 0, то число является четным, иначе — нечетным. Полученные группы чисел можно вывести отдельно, перечислив их через запятую.
3. Воспользоваться таблицей умножения. Четные числа получаются при умножении четного числа на четное число, а нечетные — при умножении четного числа на нечетное число. Таким образом, можно создать таблицу умножения и выделить в ней четные и нечетные результаты умножения.

Независимо от выбранного способа можно получить нечетные и четные цифры от 1 до 1000, через запятую, указав условия проверки четности при написании программного кода или использовании таблицы умножения.

Ручной подсчет

Если вы заинтересованы в разделении четных и нечетных цифр от 1 до 1000, вы можете провести ручной подсчет, чтобы получить результаты. Для этого вам понадобится тетрадь с карандашом (или компьютер и текстовый редактор), терпение и внимательность.

Вы можете начать с единицы и последовательно перебирать все числа до 1000. Для каждого числа вы будете определять, является ли оно четным или нечетным. Чтобы это сделать, вы должны проверить, делится ли число на 2 без остатка.

Например, для числа 1 проверка выглядит следующим образом: 1 / 2 = 0 с остатком 1. Остатком является число, которое остается после деления. Если остаток равен 0, значит, число четное, в противном случае — нечетное.

Вы можете записывать результаты в таблицу, используя теги таблицы HTML. В первом столбце таблицы выписывайте числа от 1 до 1000, а во втором столбце отмечайте, является ли число четным или нечетным.

Число	Четное/Нечетное
1	Нечетное
2	Четное
3	Нечетное
4	Четное
…	…

Продолжайте этот процесс, пока не переберете все числа от 1 до 1000. В результате получите полный список четных и нечетных чисел в пределах от 1 до 1000, перечисленных через запятую.

Таким образом, ручной подсчет позволяет детально изучить свойства чисел от 1 до 1000 и понять, какие из них являются четными, а какие — нечетными.

Использование программного кода

Для получения списка четных и нечетных цифр от 1 до 1000 можно использовать программный код. Ниже приведен пример кода на языке Python:

Программный код выше создает список всех цифр от 1 до 1000 с помощью функции range(). Затем используются условные выражения для фильтрации списка на нечетные и четные цифры. Результаты выводятся с помощью функции print().

Таким образом, применение программного кода позволяет легко получить отдельные списки нечетных и четных цифр от 1 до 1000.

Поиск в интернете

В интернете можно найти множество ресурсов, которые помогут вам найти нечетные и четные цифры от 1 до 1000, перечисленные через запятую. Где искать эту информацию?

• Используйте поисковые системы, такие как Google, Yandex, Bing и другие. Введите в поисковую строку запрос, например «нечетные и четные цифры 1-1000 перечисленные через запятую».
• Попробуйте посетить различные образовательные и математические сайты. Они часто предлагают таблицы и списки нужной информации.
• Изучите учебники по математике или задачники, в которых могут быть перечислены нечетные и четные числа.

Примерный результат поиска:

Нечетные цифры:	1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99, …
Четные цифры:	2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, …

Надеемся, что данная информация будет полезной для вас в изучении нечетных и четных цифр.