Что такое четное число

Проверка числа на четность или нечетность на C++

В этом примере оператор if … else используется для проверки того, является ли введенное пользователем число четным или нечетным в C++.

Целые числа, которые полностью делятся на 2, называются четными числами. А те целые числа, которые не делятся на 2 полностью, называются нечетными.

Чтобы проверить на C++, является ли целое число четным или нечетным, остаток вычисляется при делении его на 2 с использованием оператора %. Если остаток равен нулю, это целое число является четным, если нет, то это целое число нечетным.

Оператор if..else в С++ используется для проверки истинности n% 2 == 0. Если это выражение truth, то n – четное, если нет, то n – нечетное.

Вы также можете использовать тернарные операторы, вместо оператора if..else. Тернарный оператор – это сокращенная запись оператора if … else.

Способы получения нечетных и четных цифр

Для получения четных и нечетных цифр от 1 до 1000 через запятую можно использовать различные способы. Вот несколько из них:

1. Использовать цикл для перебора всех чисел от 1 до 1000 и проверки их на четность или нечетность. Четные числа можно сохранить в отдельную переменную или массив и затем вывести их через запятую. Аналогично можно поступить с нечетными числами.
2. Разделить все числа от 1 до 1000 на две группы: четные и нечетные. Для этого можно использовать операцию деления по модулю на 2. Если результат операции равен 0, то число является четным, иначе — нечетным. Полученные группы чисел можно вывести отдельно, перечислив их через запятую.
3. Воспользоваться таблицей умножения. Четные числа получаются при умножении четного числа на четное число, а нечетные — при умножении четного числа на нечетное число. Таким образом, можно создать таблицу умножения и выделить в ней четные и нечетные результаты умножения.

Независимо от выбранного способа можно получить нечетные и четные цифры от 1 до 1000, через запятую, указав условия проверки четности при написании программного кода или использовании таблицы умножения.

Ручной подсчет

Если вы заинтересованы в разделении четных и нечетных цифр от 1 до 1000, вы можете провести ручной подсчет, чтобы получить результаты. Для этого вам понадобится тетрадь с карандашом (или компьютер и текстовый редактор), терпение и внимательность.

Вы можете начать с единицы и последовательно перебирать все числа до 1000. Для каждого числа вы будете определять, является ли оно четным или нечетным. Чтобы это сделать, вы должны проверить, делится ли число на 2 без остатка.

Например, для числа 1 проверка выглядит следующим образом: 1 / 2 = 0 с остатком 1. Остатком является число, которое остается после деления. Если остаток равен 0, значит, число четное, в противном случае — нечетное.

Вы можете записывать результаты в таблицу, используя теги таблицы HTML. В первом столбце таблицы выписывайте числа от 1 до 1000, а во втором столбце отмечайте, является ли число четным или нечетным.

Число	Четное/Нечетное
1	Нечетное
2	Четное
3	Нечетное
4	Четное
…	…

Продолжайте этот процесс, пока не переберете все числа от 1 до 1000. В результате получите полный список четных и нечетных чисел в пределах от 1 до 1000, перечисленных через запятую.

Таким образом, ручной подсчет позволяет детально изучить свойства чисел от 1 до 1000 и понять, какие из них являются четными, а какие — нечетными.

Использование программного кода

Для получения списка четных и нечетных цифр от 1 до 1000 можно использовать программный код. Ниже приведен пример кода на языке Python:

Программный код выше создает список всех цифр от 1 до 1000 с помощью функции range(). Затем используются условные выражения для фильтрации списка на нечетные и четные цифры. Результаты выводятся с помощью функции print().

Таким образом, применение программного кода позволяет легко получить отдельные списки нечетных и четных цифр от 1 до 1000.

Поиск в интернете

В интернете можно найти множество ресурсов, которые помогут вам найти нечетные и четные цифры от 1 до 1000, перечисленные через запятую. Где искать эту информацию?

• Используйте поисковые системы, такие как Google, Yandex, Bing и другие. Введите в поисковую строку запрос, например «нечетные и четные цифры 1-1000 перечисленные через запятую».
• Попробуйте посетить различные образовательные и математические сайты. Они часто предлагают таблицы и списки нужной информации.
• Изучите учебники по математике или задачники, в которых могут быть перечислены нечетные и четные числа.

Примерный результат поиска:

Нечетные цифры:	1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99, …
Четные цифры:	2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, …

Надеемся, что данная информация будет полезной для вас в изучении нечетных и четных цифр.

Чётные и нечётные числа — Википедия

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.

Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .

С точки зрения теории сравнений, чётные и нечётные числа — это элементы соответственно классов вычетов и по модулю 2.

• Деление:
  • Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным)
  • Чётное / Нечётное = если результат — целое число, то оно Чётное
  • Нечётное / Чётное — результат не может быть целым числом, и соответственно обладать атрибутами чётности не может
  • Нечётное / Нечётное = если результат — целое число, то оно Нечётное

Сложение и вычитание: Чётное ± Чётное = Чётное Чётное ± Нечётное = Нечётное Нечётное ± Нечётное = Чётное

Умножение: Чётное × Чётное = Чётное Чётное × Нечётное = Чётное Нечётное × Нечётное = Нечётное

Признак чётности

В десятичной системе счисления

Если в десятичной форме записи числа последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.

42, 104, 1111, 9115817342 — чётные числа.

31, 75, 703, 78527, 2356895125 — нечётные числа.

В других системах счисления

Для всех систем счисления с чётным основанием (например, для шестнадцатеричной), действует тот же признак чётности: число делится на 2, если его последняя цифра делится на 2.
Для систем счисления с нечётным основанием существует другой признак чётности: число чётно тогда и только тогда, когда чётна сумма его цифр.
Например, число, обозначаемое записью «136», чётно в любой системе счисления, начиная с семеричной.

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь», а нечётные — «ян».

В разных странах существуют связанные с количеством даримых цветов традиции. Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье. В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.

В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)

В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.

С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.

Согласно Правилам дорожного движения, в зависимости от чётности или нечётности числа месяца может быть разрешена стоянка под знаками 3.29, 3.30.

• Последовательность A005408 в OEIS: нечётные числа
• Последовательность A005843 в OEIS: чётные числа
• Последовательность A179082 в OEIS: чётные числа с чётной суммой цифр в десятичной записи

Зависимость между числом и его четностью

Для определения четности числа необходимо проверить его последнюю цифру. Если последняя цифра числа равна 0, 2, 4, 6 или 8, то число является четным. Если последняя цифра числа равна 1, 3, 5, 7 или 9, то число является нечетным.

Например, число 24 является четным, так как его последняя цифра равна 4. А число 37 является нечетным, так как его последняя цифра равна 7.

Знание четности числа имеет практическую значимость в различных областях, таких как программирование, математика и физика. Например, в программировании можно использовать операцию «деление по модулю» для проверки четности числа.

Стоянка по четным и нечетным числам месяца в 2022 году

ВРЕМЯ ЧТЕНИЯ2 МИН.

02.04.2022

Рассмотрим дорожные знаки запрещающие стоянку по четным и нечетным дням.

В отличии от запрещающего знака 3.27 «Остановка запрещена», который запрещает любую остановку, знаки 3.28 «Стоянка запрещена», 3.29 «Стоянка запрещена по нечетным числам месяца» и 3.30 «Стоянка запрещена по четным числам месяца» запрещают прекращение движения продолжительностью более 5 минут, которое не связано с посадкой (высадкой) пассажиров или загрузкой (разгрузкой) транспортного средства. То есть, если необходимо остановиться в зоне действия знаков запрещающих стоянку, например для посадки пассажиров и такая остановка займет более пяти минут, то это не будет являться нарушением Правил.

3.28 «Стоянка запрещена». Запрещается стоянка транспортных средств.

3.29 «Стоянка запрещена по нечетным числам месяца».

3.30 «Стоянка запрещена по четным числам месяца».

Мы остановимся на ситуации, когда на проезжей части дороги, на ее противоположных сторонах установлены одновременно знаки  3.29 «Стоянка запрещена по нечетным числам месяца» и 3.30 «Стоянка запрещена по четным числам месяца».

При таком применении знаков, стоянка запрещена по четным и нечетным дням на соответствующей стороне проезжей части дороги.

На снимке, знаки 3.29 «Стоянка запрещена по нечетным числам месяца» и 3.30 «Стоянка запрещена по четным числам месяца» установлены на противоположных сторонах. Автомобили поставлены на стоянку также на обеих сторонах проезжей части дороги. В зависимости от числа месяца (четное или нечетное), на одной из сторон дороги, автомобили будут припаркованы с нарушением Правил.

Согласно Правилам, при одновременном применении знаков 3.29 и 3.30 на противоположных сторонах дороги, в период времени с 19 часов до 21 часа, разрешается поставить транспортное средство на стоянку на любой стороне проезжей части.

Это сделано для того, чтобы владельцы транспортных средств в конце дня могли спокойно переставить свои автомобили на соответствующую сторону проезжей части дороги в соответствии с наступающими сутками. Соответственно, следующие сутки для стоянки, в соответствии с Правилами при одновременном применении знаков  3.29 и 3.30, наступают в 21 час.

Рассмотрим на примере (изображение ниже).

Сегодня 1 число месяца (нечетное число), следовательно поставить автомобиль на стоянку разрешено на правой стороне проезжей части. Если планируем оставить транспортное средство для стоянки и на следующие сутки (четное число), то в соответствии с Правилами после 21 часа, автомобиль должен быть припаркован уже на противоположной стороне (на левой стороне) проезжей части. Перестановку транспортного средства необходимо выполнить с 19 часов до 21 часа. 

Почему время перестановки именно такое, это сделано для удобства владельцев транспортных средств, чтобы в конце рабочего или выходного дня можно было спокойно поставить автомобиль на стоянку и не делать это в 00 часов 00 минут, когда наступят следующие календарные сутки.

Опубликовано 08 октября 2019 года, обновлено 08 сентября 2020 года.

Характеристика парности у ноля

Не бывает целых чисел, которые не принадлежат к одной из групп по признаку кратности двум. Ноль, который разделяет отрицательные и положительные значения последовательного ряда, не является целым. Из-за этого большинство предполагает, что ноль стоит особняком, т. е. не относится ни к одному виду или же одновременно представляет оба.

В науке ноль — это аддитивный нейтральный элемент четной группы. Он является логическим началом для рекурсии последовательного ряда кратных двум объектов. Исследования, проведенные в учебных заведениях Великобритании, показали, что 2/3 преподавателей не знают верного ответа, а ученики пятого класса ошибаются реже, чем из шестого и старше.

Признаки четности ноля:

1. элемент гармонично вписывается в логику порядка последовательной оси натуральных и обратных числительных;
2. полное соответствие всем арифметическим законам для группы;
3. если объект, для которого нужно определить парность, двузначный и больше, цифра в конце явно указывает на кратность его двум;
4. принадлежность цифры к группе обеспечивает мультипликативность функции Мебиуса и не нарушает логику работы формулы вращения.

Маленьким слушателям легче пояснить феномен с помощью двух таблиц — по одной для каждой группы. Элементы кратных схематически изображаются в первом столбце, во втором — остаток. Олицетворяемая нолем пустота при делении на два остается пустотой, что соответствует признаку кратности двум. Вышеприведенный список доказательств содержит другие примеры для наглядной демонстрации логики принадлежности знака к группе элементов, кратных двум.

Задачи для практики

Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.

Задачка 1. Назовите числа, которые спрятаны за . Назовите их по порядку. Какие из них — четные, а какие — нечетные?

1		17
2	10
	11	19
4		20
5	13
	14	22
7	15	23
8

Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.

Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.

X	2	4	6	8	10
X × 2
X : 2

X	2	4	6	8	10
X × 2	4	8	12	16	20
X : 2	1	2	3	4	5

2 × 2 = 4 — четное 2 : 2 = 1 — нечетное 4 × 2 = 8 — четное 4 : 2 = 2 — четное 6 × 2 = 12 — четное 6 : 2 = 3 — нечетное 8 × 2 = 16 — четное 8 : 2 = 4 — нечетное 10 × 2 = 20 — четное 10 : 2 = 5 — нечетное

Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?

Посчитаем, сколько в сумме конфет шоколадных и с карамелью: 15 + 12 = 27 (к)

Отнимем от общего количества конфет получившееся число: 44 — 27 = 17 (к)

Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.

Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?

51 — 5 = 46 (ф) 46 — четное число.

Ответ: изначально у Маши в инстаграме было 46 фотографий.

Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.

1	☆	3	☆	5
6	☆	☆	9	10
☆	12	13	☆	15
16	☆	☆	19	20
☆	22	23	☆	25

Ответ: 2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.

Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70

Затем складываем нечетные: 7 + 11 + 17 + 21 = 56 70 + 56 = 126 Число 126 оканчивается на четную цифру 6. Значит, число 126 — четное.

Большая энциклопедия школьника

Большая энциклопедия школьникауникальное издание, содержащее весь свод знаний,
необходимый ученикам младших классов. Для детей, собирающихся в 1-й класс, она послужит незаменимым
помощником для подготовки к школе. В этой энциклопедии ребенок сможет найти любую интересующую его информацию,
в понятном и простом для него изложении. Вы подбираете слова и определения для простых вещей,
которые надо объяснить ребенку? Сомневаетесь в формулировках? Просто возьмите

Математика в стихах
Развитие речи
Азбука в картинках
Игры на развитие внимания
Как правильно выбрать школу
Ваш ребенок левша
Как готовить домашнее задание
Контрольные и экзамены

Большая энциклопедия школьника – это твой надёжный путеводитель в мире знаний.
Она проведёт сквозь извилистые лабиринты наук и раскроет завесу великих тайн Вселенной.
С ней ты поднимешься высоко к звёздам и опустишься на дно самых глубоких морей,
ты научишься видеть мельчайшие организмы и осязать огромные пространства Земли.
Отправившись в это увлекательное путешествие, ты значительно расширишь свой кругозор и поднимешься
на новую ступень развития. Отныне никакие вопросы учителей не смогут поставить тебя в тупик,
ты сможешь найти выход из любой ситуации. Мир знаний зовёт тебя. В добрый путь!

Ребенок не хочет учить буквы Ребенок не хочет учить буквы – Понимаете, ведь надо что-то делать! – с тревогой говорила мне полная, хорошо одетая дама, едва умещающаяся на стуле. Ее ноги в аккуратных лодочках были плотно сжаты (юбка до середины колена казалась слегка коротковатой для такой монументальной фигуры), руки сложены на коленях. – Ей же на тот год в школу, все ее сверстники уже читают, а она даже буквы …

Past continuous passive Страдательный залог образуется с помощью вспомогательного глагола ‘to be’. Страдательный залог глагола ‘to repair’ в группе ‘continuous’ : To be repaired = Быть исправленным. The road is being repaired = Дорогу чинят. The road is not being repaired = Дорогу не чинят. Is the road being repaired? = Чинят ли дорогу? The road was being repaired = Дорогу чинили. The road was not being repaired = Дорогу не чинили. Was the road being repaired? = Чинили ли дорогу? Страдательный …

Определение формулы органического вещества по его молярной массе Задание: Определить формулу углеводорода, если его молярная масса равна 78 г. № п/п Последовательность действий Выполнение действий 1. Записать общую формулу углеводорода. Общая формула углеводорода СхНу 2. Найти молярную массу углеводорода в общем виде. М(СхНу)=12х +у 3. Приравнять найденное в общем виде значение молярной массы к данному в …

У У ЗВУК (У). 1) Удобная буква! Удобно в ней то, Что можно на букву Повесить пальто. У – сучок, В любом лесу Ты увидишь букву У. 2) ФОНЕТИЧЕСКАЯ ЗАРЯДКА. – Как воет волк! ( у – у – у ) 3) ЗАДАНИЯ. а) Подними руку, если услышишь звук (у): паук, цветок, лужа, диван, стол, стул, голуби, курица. б) Где стоит (у)? Зубы, утка, наука, кенгуру …

Сумма, произведение, частное четных (нечетных) чисел

Утверждение 1. Сумма двух четных чисел — четное число.

Доказательство. Пусть числа m и n являются четными. Докажем, что число r = m + n также четно. m=2k, n=2p, где k и p — целые числа. Тогда r = m + n = 2k + 2p = 2(k + p) = 2s. Если числа k и p являются целыми, то их сумма s — тоже целое число. Мы доказали, что число r может быть представлено в виде произведения двойки и целого числа. Доказательство завершено.

Утверждение 2. Сумма двух нечетных чисел — четное число. Докажите самостоятельно.

Утверждение 3. Сумма четного и нечетного чисел — нечетное число. Докажите самостоятельно.

Утверждение 4. Произведение двух нечетных чисел — нечетное число.

Доказательство. Пусть числа m и n являются нечетными. Докажем, что число r = m • n также нечетно.
m = 2k + 1, n = 2p + 1, где k и p — целые числа.
Тогда r = m • n = (2k+1) • (2p+1) = 4kp + 2k + 2p + 1 = 2(2kp + k + p) + 1 = 2s + 1.
Если числа k и p являются целыми, то число s = 2kp + k + p — тоже целое число.
Мы доказали, что число r может быть представлено в виде r = 2s + 1, следовательно, является нечетным. Ч. т. д.

Утверждение 5. Произведение двух четных чисел — четное число. Докажите самостоятельно.

Утверждение 6. Произведение четного и нечетного чисел — четное число. Докажите самостоятельно.

А если мы поделим четное число на четное (не равное нулю)? Что получим: чет или нечет? Естественно, однозначного ответа дать нельзя. Например, при делении 12 на 4 мы получаем нечетный результат, а при делении 32 на 4 — четный.

Если вы уже заскучали, переходите ко 2-й части статьи. Потом всегда сможете вернуться. Если же все эти теоретические построения вас не слишком утомили, давайте продолжим.

А почему, собственно, мы рассматриваем только два числа. Давайте мыслить шире!

Утверждение 7. Сумма любого количества четных чисел четна.

Доказательство. Пусть числа M₁, M₂, …, M_N являются четными, тогда их можно представить в виде 2K₁, 2K₂, … , 2K_N, где K₁, K₂, …, K_N — целые числа.
Тогда: M₁ + M₂ + … + M_N = 2K₁ + 2K₂ + … + 2K_N = 2( K₁ + K₂ + … + K_N) = 2S, где S-целое число. Четность доказана.

Утверждение 8. Сумма четного количества нечетных чисел четна. Сумма нечетного количества нечетных чисел нечетна. Докажите самостоятельно.

Утверждение 9. Произведение может быть нечетным только в том случае, если все сомножители нечетны. Докажите самостоятельно.

Так, сумма 2+4+6+…+1022+1024 четна, поскольку все слагаемые четны. Сумма 1+3+5+7+9 нечетна, т. к. содержит 5 нечетных слагаемых. Произведение 2*3*4*…*1001*1002 четно уже хотя бы по той причине, что первый сомножитель является четным.

Задание 4. Четными или нечетными будут следующие выражения: а) 2+12+22+…+1002+1012+1022, б) 1+11+111+…+111111+1111111, в) 3*13*23*…*10003*10013*10023, г) 2*3*4*…*12357891 ?

Задание 5. Докажите, что произведение всех простых чисел, не превосходящих 1000000, четно. Докажите, что произведение любого количества простых чисел, каждое из которых больше 100, нечетно. Напомню, что натуральное число называется простым, если делится только на себя и на 1.

История и значение в культуре

Неоценимое влияние на развитие арифметики оказали труды Пифагора. Ученый посвятил много труда и времени, чтобы выявить закономерности свойств чисел и объединить их в логичную систему. Математические законы и наблюдения он связал с мировосприятием и теорией самопознания человека.

Каждой цифре математик отвел свое значение. Нечетные обладают более сильными, активными характеристиками. Именно они в воссозданной мистической системе являлись олицетворением мужского начала, динамики и солнца. Четные же, наоборот, олицетворяли женское естество, статичность и луну.

Аналогичное деление характерно для китайской философии, в которой нечетные числительные относят к светлой мужской субстанции Ян, а Инь — к теневому, негативному, женскому. В учении о материи тайцзи противоположности представлены как единые и неделимые стороны одного целого.

У каждого этноса существуют свои поверья. Самое популярное суеверие у славян запрещает преподносить букеты с парным количеством цветов. В США и Европе такой подарок, наоборот, трактуется как пожелание счастья и благополучия. Нечетность приглашенных гостей, дней празднования, даты события также считается обязательным по свадебным традициям Руси.

Четные и нечетные числа

Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.

Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.

Четное число — это число, которое делится нацело на 2.

4 : 2 = 2 Это значит, что 4 — четное число.

Нечетное число — это число, которое не делится на 2 без остатка.

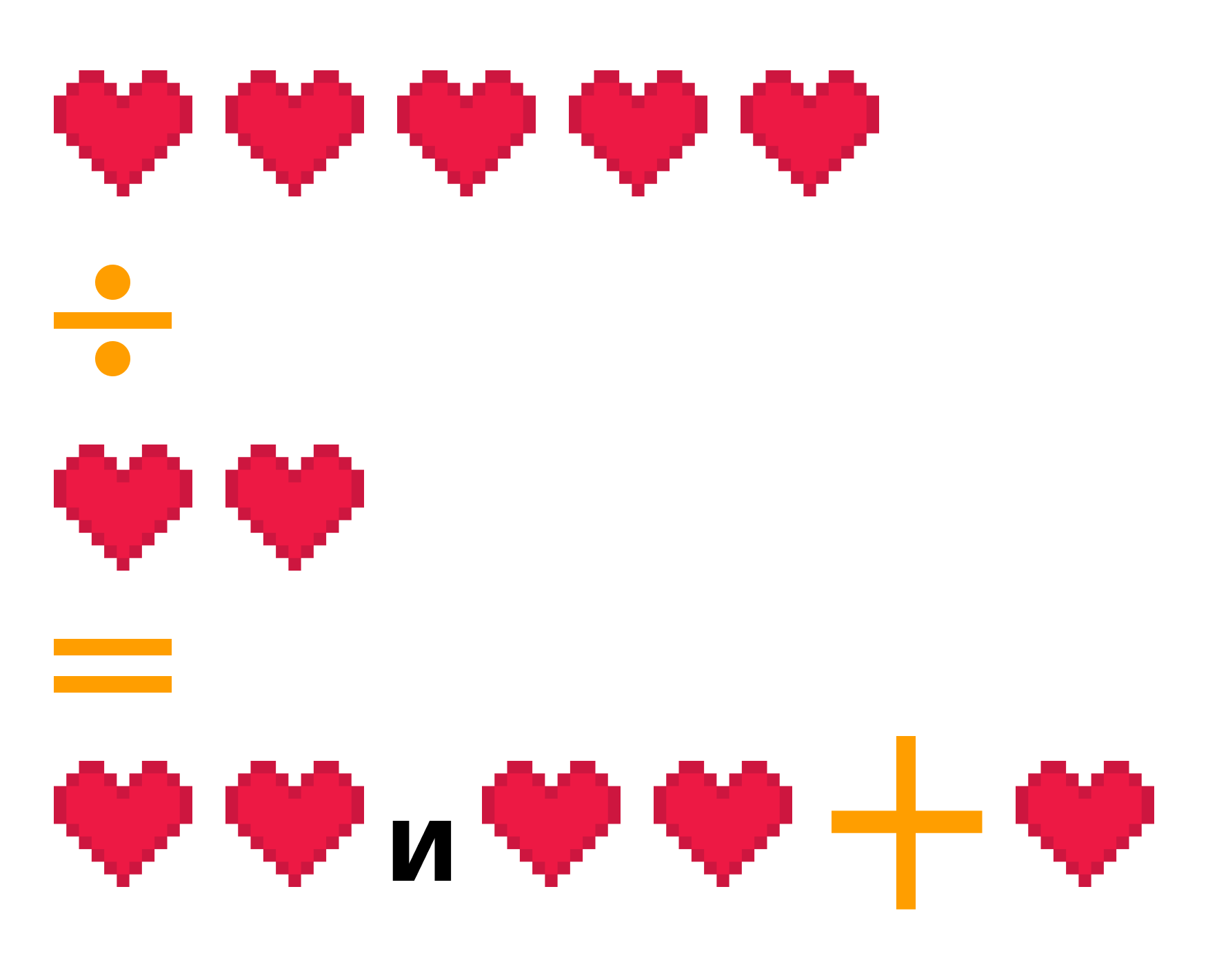
5 не делится на 2 без остатка — значит, 5 это нечетное число.

Если число оканчивается на 0, 2, 4, 6, 8, то это число четное.

Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное.

Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа.