Как научиться решать уравнения 4 класс по математике

Изучение уравнений 4 класса

Изучение уравнений в 4 классе является важным шагом в развитии математических навыков у ребенка. Решение уравнений помогает развивать логическое мышление и умение анализировать задачи.

Уравнения 4 класса — это уравнения с одной переменной, которые можно решить путем переноса чисел и знаков через знак равенства. Для решения уравнений 4 класса требуется знание основных математических операций: сложение, вычитание, умножение и деление.

Один из методов решения уравнений 4 класса — это метод баланса. Этот метод заключается в том, чтобы использовать обе стороны уравнения как части весов на балансе, и попробовать добавить, вычесть, умножить или разделить обе стороны, чтобы свершить равновесие.

Для того, чтобы научиться решать уравнения 4 класса, нужно часто практиковаться и решать множество задач разной сложности. Разработчики учебных пособий и заданий стараются представить материал в интересной игровой форме, включая головоломки и задачки на логику.

Как объяснить решение уравнений с х (икс) школьнику в 4 классе?

Обратите внимание! В левом столбце печатного материала находятся: теоретические материалы;. краткая запись теоретических положений

В правом столбце печатного материала находятся: графическая иллюстрация к теоретическому материалу. Материал содержит три разобранных задачи и девять.

Задачи на тему: «Задачи на уравнение. Решение уравнений, примеры»

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Решение уравнений

1. Реши уравнения на сложение и вычитание целых чисел.

2. Реши уравнения на умножение и деление целых чисел.

3. Реши уравнения на сложение и вычитание дробей.

4. Реши уравнения на умножение и деление дробей.

Текстовые задачи и уравнения

Составь уравнения к задачам и реши их.

1. Автобус проехал 2 часа со скоростью 60 км/час и ещё 3 часа – со скоростью 70 км/час. Какое расстояние проехал автобус за все время?

УРОКИ И ПРЕЗЕНТАЦИИ

Материалы сайта — оригинальные, не скопированы из других источников (учебников, задачников, сайтов, ресурсов и т. д.) Они разработаны в строгом соответствии с ФГОС конкретного автора или темы.

Все права защищены. Запрещено любое копирование материалов сайта без письменного согласия владельцев ресурса!

Математика 4 класс. Задачи, решения, ответы.

Задачи по математике 4 класс.

Задание 1:

В магазин привезли 32 коробки конфет, по 9 кг в каждой, и 36 коробок вафель, по 8 кг в каждой. Каких сладостей привезли больше и на сколько килограммов больше?

Решение:1) 32 * 9 = 288 2) 36 * 8 = 288
Ответ: В магазин привезли одинаковое количество конфет и вафель.

Задание 2:

С одного поля собрали 1 т 800 кг картофеля, а с другого — в 3 раза меньше. Весь картофель разложили в мешки, по 40 кг в каждый. Сколько мешков с картофелем получили?

Решение:1)1800 : 3 = 600 (со второго поля) 2) 1800 + 600 = 2400 (всего собрали картофеля) 3) 2400 : 40 = 60(мешков с картофелем получили)
Ответ: 60 мешков.

Задание 3:

• 1) Вычисли периметр и площадь прямоугольника со сторонами 2 см и 4 см.
• 2) Найди длину стороны квадрата, периметр которого равен периметру прямоугольника в задании 1).

Решение:1) 2 + 2 + 4 + 4 = 12 см (периметр прямоугольника), 2 * 4 = 8 квадратных сантиметра
2) 12 : 4 = 3 (длина стороны квадрата)

Задание 4:

Один мастер изготовил 6 ниток бус, по 38 бусинок в каждой, а другой — 7 ниток бус, по 36 бусинок в каждой. Какой мастер использовал больше бусинок и на сколько?

Решение:1) 6 * 38 = 228 (бусинки использовал 1 мастер) 2) 7 * 36 = 252 (бусинки использовал 2 мастер) 3) 252 — 228 = 24
Ответ: Второй мастер использовал на 24 бусинки больше чем первый.

Задание 5:

В первый день в санаторий приехало 900 человек, а во второй — в 9 раз меньше, чем в первый. Всех отдыхающих поселили в комнаты, по 2 человека в каждой. Сколько комнат заняли все отдыхающие?

Решение:1) 900 : 9 = 100 (отдыхающих приехало во второй день) 2) 900 + 100 = 1000 (отдыхающих приехало за 2 дня) 3) 1000 : 2 = 500 (комнат заняли все отдыхающие) Ответ: 500 комнат.

Задание 6:

• 1) Вычисли периметр и площадь прямоугольника со сторонами 7 см и 3 см.
• 2) Найди длину стороны квадрата, периметр которого равен периметру прямоугольника в № 1).

Решение:1) 7 + 7 + 3 + 3 = 20 см (периметр), 7 * 3 = 21 см квадратных (площадь)
2) 20 : 4 = 5(длина стороны квадрата)
Задачи повышенной сложности по математике 4 класс.

Задание 1:

Один токарь за смену изготовил 32 детали. Другой токарь, работая с той же производительностью, изготовил 24 детали. Сколько часов работал первый токарь, если известно, что второй токарь работал на 2 часа меньше, чем первый?

Решение:

Пусть первый токарь работал x часов. Тогда второй токарь работал (x — 2) часов. Первый токарь за час изготавливал (32/x) деталей, а второй токарь (24/(x — 2)). По условию задачи оба токаря работали с одинаковой производительностью. Это значит, что за 1 час они изготавливали одинаковое число деталей, поэтому мы можем записать и решить уравнение: 30/x = 24/(x — 2); 32*(x — 2) = 24 * x; 32x — 64 = 24x; 8x = 64; x = 8.Ответ: первый токарь работал 8 часов.

Задание 2:

Сложная задача по математике для 4 класса: Из двух городов по реке одновременно выплыли навстречу друг другу две моторные лодки. Скорость первой лодки 15км/ч, второй лодки 35км/ч. Первая лодка двигалась по течению реки. Скорость течения реки 5км/ч. Через сколько часов лодки встретились, если расстояние между городами 250км?

Решение:

Пусть до встречи лодок первая проплыла x км. Тогда вторая лодка проплыла (250 — x) км. Учитывая скорость течения реки, скорость первой лодки 15 + 5 = 20км/ч. Соответственно, скорость второй лодки 35 — 5 = 30км/ч. Очевидно, что время в пути до встречи одинаково, поэтому можно записать уравнение: x/20 = (250 — x)/30; x * 30 = 20 * (250 — x); 30x = 5000 — 20x; 50x = 5000; x = 100км.

Первая лодка до встречи со второй прошла 100км. Рассчитаем время: t = x/20 = 100/20 = 5ч.

Для проверки мы можем рассчитать время второй лодки: t = x/20 = (250 — x)/30 = 150/30 = 5ч. Ответ: лодки встретились через 5 часов.

Задания по математике 4 класс:

Тест 1       |       Тест 2       |       Тест 3       |       Тест 4       |       Тест 5

Сложные уравнения. 4 класс

38 000 репетиторов из РФ и СНГ

Занятия онлайн и оффлайн

Более 90 дисциплин

Быстрый и безопасный, простой в использовании Яндекс Браузер

Устанавливая рекомендуемое программное обеспечение, вы соглашаетесь с лицензионными соглашениями Яндекс.Браузера и настольного ПО Яндекса.

1) 3074 + а : 8 = 3524

2) 9 х Х + 59968 = 61354

4) 5890 – а : 4 = 5290

5) 157 + Х х 6 = 25705

6) ( Х + 127) х 12 = 8460

7) ( 169 х с ) : 35 = 845

Х : 158 + 106 = 315

9) 57165 –Х : 115 = 57104

10) (с + 7412) – 4246 = 10231

11) 8345 + Х : 716 = 8271

12) ( а + 532) х 306 = 290700

13) с х 215 – 4933 = 63222

14) 10002 – 3105 : Х = 9933

15) ( Х + 736) х 24 = 21888

16) 75 х Х + 8569 = 17869

17) Х х 92 – 12917 = 33267

18) 7 х (5115 – с) = 9156

19) (Х – 63580) : 5 = 3107

20) ( 5289 – а) + 3563 = 7001

21) 56 х Х + 287 = 791

22) а х 8 – 29134 = 18890

23) 2947 + (Х – 845) = 4773

24) 6834 – (Х :245) = 6816

25) 5800 + 9 х Х = 11227

Выберите книгу со скидкой:

ОГЭ. География. Новый полный справочник для подготовки к ОГЭ

Математика. Новый полный справочник школьника для подготовки к ЕГЭ

Дошкольная педагогика с основами методик воспитания и обучения. Учебник для вузов. Стандарт третьего поколения. 2-е изд.

Считаю и решаю: для детей 5-6 лет. Ч. 1, 2-е изд., испр. и перераб.

Начинаю считать: для детей 4-5 лет. Ч. 1, 2-е изд., испр. и перераб.

Считаю и решаю: для детей 5-6 лет. Ч. 2, 2-е изд., испр. и перераб.

Пишу буквы: для детей 5-6 лет. Ч. 2. 2-е изд, испр. и перераб.

Русско-английский словарик в картинках для начальной школы

ОГЭ. Литература. Новый полный справочник для подготовки к ОГЭ

ЕГЭ. Английский язык. Новый полный справочник для подготовки к ЕГЭ

Рисуем по клеточкам и точкам

ЕГЭ. Информатика. Новый полный справочник для подготовки к ЕГЭ

БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА

Инфолавка – книжный магазин для педагогов и родителей от проекта «Инфоурок»

VI Международный дистанционный конкурс «Старт»

• 16 предметов
• Для учеников 1-11 классов и дошкольников
• Наградные и подарки

Международные дистанционные “ШКОЛЬНЫЕ ИНФОКОНКУРСЫ”

для дошкольников и учеников 1–11 классов

Оргвзнос: от 15 руб.

Номер материала: ДБ-772270

Добавляйте авторские материалы и получите призы от Инфоурок

Призовой фонд 200 000 руб.

Не нашли то что искали?

Вам будут интересны эти курсы:

Шаг 1: Упрощение уравнения

Перед тем как начать решение уравнения 4 класса, необходимо упростить его для облегчения дальнейших вычислений. В этом шаге мы избавляемся от ненужных членов и приводим уравнение к более простому виду.

Для начала, давайте рассмотрим типичное уравнение 4 класса:

5x + 3 = 18x — 2

В данном уравнении мы имеем две переменные: x и числовые значения 5, 3, 18 и 2. Чтобы упростить уравнение, мы будем следовать нескольким шагам:

Шаг 1: Сгруппируйте все члены с переменной x на одной стороне, а все члены без переменной x на другой стороне уравнения.

5x — 18x = -3 — 2

В результате этого шага у нас остаются переменные x только на одной стороне уравнения.

Шаг 2: Приведите переменные x на одной стороне уравнения.

-13x = -5

Теперь мы получили уравнение, где x находится только на левой стороне.

Шаг 3: Решите уравнение относительно переменной x.

Для этого мы делим обе стороны уравнения на коэффициент при x:

x = -5 / -13

Таким образом, получаем ответ:

x = 5/13

Мы успешно упростили уравнение и нашли его решение. В следующих шагах мы рассмотрим, как проверить правильность решения и как возможно упростить уравнение еще больше.

Как решать задачи на время 4 класс

Чтобы вычислить время движения, нужно расстояние разделить на скорость t = S : V.

По формуле 36 км : 12 км/ч = 3 часа.

Пешеход идет со скоростью 6 км/ч. С этой скоростью он двигался 30 км. С какой скоростью идет лыжник, если за такое же время он проходит 50 км? Сколько времени в пути находится лыжник?

Составим краткую запись:

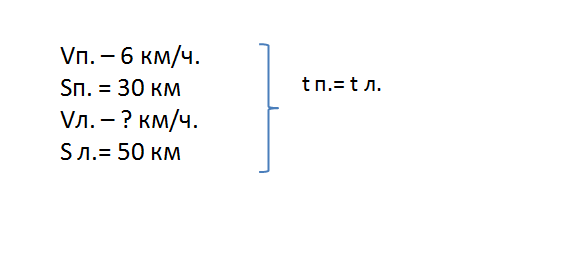
Чтобы узнать скорость лыжника, сначала мы должны узнать время в пути. Для этого используем данные пешехода, так как время в пути у них одинаковое.

1. t п. = 30 : 6 = 5 часов.
2. V л. = 50 : 5 = 10 км/ч.

Ответ: 10 км/ч; 5 ч.

Так же в четвертом классе решают задачи на время, не связанные с движением.

Уверенное решение уравнений 4 класса

Для многих учеников начальной школы решение уравнений может представлять трудность. Однако, с правильным подходом и достаточным количеством практики, решать уравнения 4 класса может быть легко и даже интересно.

Для начала, ученикам нужно усвоить правила решения простейших уравнений, например: x + 3 = 7; 8 — y = 2 и т.д. Решение таких уравнений основывается на определенных математических принципах, которые нужно понимать, чтобы решать уравнения правильно.

Для уверенного решения уравнений 4 класса, предлагается много практических заданий, которые помогут закрепить теоретические знания и улучшить навыки решения. Кроме того, можно использовать специальные онлайн-ресурсы и задания, которые помогут ученикам решать уравнения на компьютере, что будет еще более интересно и увлекательно.

Стоит заметить, что уравнения 4 класса не являются сложными по сравнению с уравнениями более продвинутых классов, однако, они являются важной основой для дальнейшего изучения математики. Поэтому, уверенное решение уравнений 4 класса — это важный шаг на пути к успешному обучению математике в дальнейшем

Работа с примерами

Для того чтобы научиться решать уравнения, очень важно уметь работать с примерами. Нужно понимать, какие операции происходят в каждом уравнении, какие действия можно проводить, чтобы избавиться от неизвестной величины

При решении примеров нужно следить за тем, чтобы обе стороны уравнения оставались равными. Для этого можно использовать различные действия, например, сложение или вычитание одного и того же числа с обеих сторон уравнения.

Также очень важно уметь правильно читать и понимать условие задачи

Нужно обратить внимание на ключевые слова, которые могут указывать на необходимость решения уравнения. Например, слова «сколько всего», «осталось», «было» и т.д

Не стоит забывать, что решение уравнения может получиться нецелым числом. В этом случае нужно округлять ответ до нужного количества знаков после запятой.

Для тренировки работы с примерами можно использовать различные методические пособия или просто составлять уравнения на основе реальных жизненных ситуаций.

Почему ГДЗ по математике полезны для четвероклассников?

Четвертый класс является своеобразным переломным моментом, ведь заканчивается начальная школа. В таком возрасте единственное, чем действительно можно привлечь школьников к обучению — это хорошие оценки. В этом поможет пособие с ответами по математике для 4 класса, где собраны решения ко всем домашним заданиям, предусмотренные на этот год. Книгой пользоваться очень просто и эффективно, оно подойдет и для юных математиков и для тех, кто имеет успехи меньше. Алгоритм использования такой: сначала ребенок решает самостоятельно задание, далее проверяет с помощью ГДЗ, а при нахождении неправильных ответов, переписывает их из надежного источника и проводит анализ над допущенными неточностями. Такой метод определит наличие всех проблем, и на дополнительных занятиях можно будет изучать именно такие темы.

В старших классах этот предмет будет разделен на алгебру и геометрию, совсем не похожих на те, что сейчас изучают. Поэтому стоит своевременно усвоить основы и уверенно шагать дальше по школьной программе. Наш портал интуитивно удобен, поэтому трудностей в использовании не будет. Пособие соответствует учебнику 2020 года под редакцией Моро М.И., поэтому в актуальности также не нужно сомневаться. Можно забыть о долгих поисках соответствующей книги по книжным магазинам и о неоправданных цены на них, а также о габаритах решебников и несоответствии готовых задач с учебником. Если ребенок уже сейчас начнет выполнять домашние задания предложенным методом, то начнет развиваться самостоятельно, что бесспорно будет полезно для дальнейшего обучения.

Примеры решений

Решение:

Пусть $x$ — количество монет в мешке, а значит в сундуке: $3x$ монет.
После того, как из мешка переложили $24$ монеты, в сундуке стало: $3x+24$, а в мешке $x-24$. И если в сундуке их стало в $7$ раз больше чем в мешке, то имеем: $3x+24=7(x-24)$.

Ну вот мы и составили уравнение (математическую модель), осталось решить уравнение относительно $x$ и записать ответ.

Решим полученное уравнение: $3x+24=7(x-24)$. Легко увидеть, что уравнение является линейным (узнать как решаются линейные уравнения можно тут.)

Раскроем скобки в правой части уравнения: $3x+24=7x-7\cdot 24$. Перенесём все слагаемые содержащие переменную в правую часть, а всё что не содержит $x$ в левую, получим: $24+7\cdot 24=7x-3x$. После упрощения получили $192=4x$, разделим обе части уравнения на коэффициент при неизвестном, т.е на $4$, тогда получим $x=48$.

Решение:

Пусть в первый мешок насыпали $3x$ кг муки, тогда во второй мешок насыпали $x$ кг. Если сложим количество кг в каждом мешке, то получим $3600$ кг муки. Имеем: $3x+x+800=3600$, решим уравнение классическим методом.

Все слагаемые содержащие $x$ оставим слева, а всё остальное перенесём в правую часть равенства: $3x+x=3600-800$, упростим обе части; $4x=2800$ поделим обе части равенства на $4$ и получим ответ: $x=700$.

Решение:

Пусть во втором мешке $x$ кг картофеля, тогда в первом мешке $4x$ кг. Из первого взяли $40$ кг, тогда в первом стало: $4x-40$. Во второй мешок насыпали $5$ кг и теперь в нём: $x+5$ кг картошки. Нам известно, что после этих изменений количество картофеля в мешках стало поровну, запишем это с помощью линейного уравнения:

$$4x-40=x+5$$

Решим это линейное уравнение. Все слагаемые содержащие переменную перенесём влево, а свободные члены вправо и получим:

$$4x-x=5+40$$

Упростим выражения:

$$3x=45$$

Избавимся от коэффициента при неизвестном и получим ответ:

$$x=15$$

Решение:

Пусть машины едут со скоростью $v$ км/ч, тогда после ускорения первой машины её скорость стала: $v+20$ км/ч, а скорость второй машины после замедления стала: $v-20$ км/ч. Нам известно по условию, что после изменения скоростей машин, первая проходит за два часа ровно столько, сколько вторая за четыре, тогда имеем:

По известной нам формуле $S=vt$ ($S$ — расстояние, $v$ — скорость, $t$ — время)

$$2(v+20)=4(v-20)$$

Сократим обе части равенства на $2$, тогда получим: $v+20=2(v-20)$. Раскроем скобки в правой части уравнения и сгруппируем все переменные в правой части равенства.

$$v+20=2v-2\cdot 20$$

$$v+20=2v-40$$

$$20+40=2v-v$$

$$v=60$$

Решение:

Пусть во вторую бригаду привезли $x$ кг раствора цемента, тогда в первую бригаду привезли $x-50$ кг. Через 3 часа работы у первой бригады осталось $x-50-3\cdot 150$ кг цемента, а у второй $x-3\cdot 200$ кг.

По условию известно, что через 3 часа работы в первой бригаде осталось в 1,5 раза больше цемента, чем во второй, тогда имеем:

$$x-50-3\cdot 150=1,5(x-3\cdot 200)$$

Осталось решить данное уравнение относительно $x$ и истолковать ответ.

Упростим и раскроем скобки в правой части, тогда получим:

$$x-500=1,5x-1,5\cdot 600$$

Если вам неудобно работать с десятичными дробями, то вы всегда можете их переводить в рациональный вид: $1,5=\frac{15}{10}=\frac{3}{2}$.

Запишем с учётом перевода дробей и упростим:

$$x-500=\frac{3}{2}x-\frac{3}{2}\cdot \frac{600}{1}$$

$$x-500=\frac{3x}{2}-\frac{3}{1}\cdot \frac{300}{1}$$

$$x-500=\frac{3x}{2}-900$$

Перенесём слагаемые содержащие переменную в правую сторону, а всё остальное в левую:

$$900-500=\frac{3x}{2}-x$$

$$400=\frac{3x}{2}-\frac{x}{1}$$

$$400=\frac{3x-2x}{2}$$

$$400=\frac{x}{2}$$

Домножим обе части на 2 и получим ответ:

$$x=800$$

Оставьте свой комментарий

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Из своей практики

Мальчик писал так, как хотел, вопреки существующим правилам по математике. При проверке уравнения были разные цифры и одно число (с левой стороны) не равнялось другому (то что с правой стороны), он тратил время на поиски ошибки.

При вопросе, почему он так делает? Был ответ, что он пытается угадать и думает, а вдруг сделает правильно.

В данном случае нужно каждый день (через день) решать подобные примеры. Довести действия до автоматизма и конечно все дети разные, дойти может не с первого занятия.

Если у родителей нет времени, а часто это так, потому что родители зарабатывают денежные средства, то лучше найти репетитора в своём городе, который сможет объяснить пройденный материал ребёнку.

Сейчас век ЕГЭ, тестов, контрольных работ, есть дополнительные сборники и методички. Делая за ребёнка домашние задания, родители должны помнить, что на экзамене в школе их не будет. Лучше объяснить доходчиво ребёнку 1 раз, чтобы ребёнок смог самостоятельно решать примеры.

Как решать взаимосвязанные задачи 4 класс

Многие путают обратные и взаимосвязанные задачи. Во взаимосвязанных задачах решение следующей зависит от известных данных предыдущей задачи. Разберемся на примере.

Пояснение: на один костюм уходит 1 метр ткани. Не забудем это при решении второй задачи.

Задача 1.

1. 13 • 2 = 26 костюмов жуков
2. 13 — 5 = 8 костюмов бож.коровок.
3. 13 + 26 + 8 = 47 костюмов всего.

На один костюм требуется 1 метр ткани, значит на все понадобится 47 метров.

Задача 2.

47 метров ткани на костюмы, это четверть всего материала для задника сцены. Чтобы найти количество материала для сцены, нужно умножить ткань для костюмов на 4. Получается 47 • 4 = 188 метров.

Ответ: 188 метров.

Движение в противоположных направлениях

Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:

Скорость удаления больше скорости любого из них.

Задача 1

Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?

Решение:

Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.

1. 

Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.

2.

Ответ: Через три часа расстояние между переходами будет 27 км.

Задача 2

Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?

Решение:

Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:

1.

Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.

2.

Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.

3.

Ответ:Скорость второго пешехода – 4 км/ч.

Задача 3

Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?

Решение:

1) 70+45=115 (км/ч) скорость удаления поездов

2) 115∙2=230 (км) пройдут поезда вместе за 2 часа

3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.

Ответ: Через 2 часа расстояние между поездами составит 250 км.

Задача 4

Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?

Решение:

1) 60+40=100 (км/ч) скорость удаления мотоциклистов

2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.

Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.

Как решать обратные задачи 4 класс

Чтобы научиться решать обратные задачи, нужно внимательно их прочитать и ответить на два вопроса: Чем задачи похожи? Чем они отличаются? Разберемся на примере простых задач на сложение и вычитание.

Света купила 9 фломастеров, а Оля 8. Сколько всего купили фломастеров девочки?

Такая задача называется прямой.

Чтобы получилась обратная ей задача, достаточно сделать неизвестной одну из данных величин. Пусть неизвестно сколько купила фломастеров Оля.

Света и Оля покупали фломастеры, всего 17. Света купила 9 фломастеров. Сколько купила Оля ? 

В первой прямой задаче мы должны были узнать общее количество фломастеров, а в обратной задаче эта величина нам уже известна. Наоборот, требуется найти сколько купила фломастеров одна из девочек. Можно составить еще одну обратную задачу, взяв за неизвестное покупку Светы.

Как придумать и решить задачу

Для того, чтобы придумать задачу надо понимать, что у нее должен быть смысл. Чтобы задача решалась, условие и данные должны быть сформулированы верно.

В задаче должно быть минимум два данных (переменных). У Маши 4 груши, а у Тани 5.

Дальше составляется конкретное условие. Петя взял у Маши 2 груши, а у Тани 3.

После этого обязательно следует главный вопрос задачи, что именно нужно найти. Сколько груш осталось у девочек? И сколько груш стало у Пети?

Соберем все части нашей придуманной задачи, вот что получилось:

<<У Маши 4 груши, а у Тани 5. Петя взял у Маши 2 груши, а у Тани 3. Сколько груш осталось у девочек? И сколько груш стало у Пети?>>.

Иногда дается задание в виде рисунка по которому нужно придумать собственную задачу и решить ее.

Решение:

Задачу можно решить алгебраически, с помощью уравнения.

Пусть вторая полка равна Х книг. Тогда на первой полке 2•Х книг. Всего их 150. Получается уравнение:

Х + 2•Х = 150

3•Х = 150

Х = 150 : 3

Х = 50, следовательно на первой полке 50 книг, на второй 2•Х = 2•50=100 книг.