Задача 2: Прогнозирование следующего числа в последовательности
Одной из основных задач анализа ряда чисел является поиск закономерности и возможность прогнозирования следующего числа в последовательности. Часто числовые ряды возникают в различных областях, таких как физика, экономика, статистика и т.д.
Для решения данной задачи необходимо найти закономерность в ряде чисел и использовать ее для прогнозирования следующего числа. Существует несколько методов и подходов к решению данной задачи.
- Методы статистического анализа: такие методы включают в себя анализ трендов, сезонности, автокорреляции и др. Они позволяют составить модель, описывающую поведение ряда чисел и предсказать следующее число на основе полученных закономерностей.
- Математические методы: для решения данной задачи часто применяются методы математической статистики, аппроксимации функций, линейной регрессии и др. Они позволяют построить аналитическую модель, которая описывает ряд чисел и позволяет прогнозировать следующее число.
- Методы машинного обучения: с развитием и популяризацией методов машинного обучения, таких как нейронные сети, решающие деревья и др., стало возможным применять их для прогнозирования следующего числа в ряде. Путем обучения модели на исторических данных можно достичь хороших результатов в прогнозировании.
Выбор метода для решения задачи зависит от конкретной ситуации, доступных данных и допустимой точности прогноза. Однако в любом случае, решение данной задачи требует тщательного анализа ряда чисел, поиска закономерности и применения соответствующих методов и инструментов для получения прогноза.
Подзадача 1: Поиск закономерности в ряду чисел
Для того чтобы решить задачу, составленную на основе ряда чисел, необходимо сначала найти закономерность в этом ряде. Нахождение закономерности поможет понять, какие числа следуют после предыдущих и как они связаны между собой.
Одним из способов найти закономерность является анализ чисел в ряде и поиск общего правила или формулы, которая связывает эти числа. Это может быть арифметическая или геометрическая прогрессия, последовательность Фибоначчи или иная математическая закономерность. Возможно, что закономерность будет не сразу очевидна, и для ее выявления потребуется дополнительный анализ и исследование ряда чисел.
После того как закономерность в ряду чисел найдена, можно перейти к решению задачи. Закономерность позволит предсказать следующие числа в ряде и использовать их для получения нужного результата. Например, если в ряде чисел присутствует арифметическая прогрессия со шагом 2, то следующее число после 4 будет 6, а следующее число после 6 будет 8 и так далее.
Поиск закономерности в ряде чисел является важным этапом решения задачи, так как он позволяет понять, как числа связаны между собой и каким образом можно получить нужный результат. Зная закономерность, можно применить ее для решения других задач, основанных на том же ряде чисел.
Подзадача 2: Прогнозирование следующего числа
После того, как мы нашли закономерность в ряде чисел и составили формулу, мы можем использовать её для прогнозирования следующего числа в задаче. Прогнозирование позволяет нам предсказать, какое число будет следующим в ряде, не продолжая последовательность вручную.
Для решения этой подзадачи сначала необходимо найти закономерность в исходном ряде чисел. Это можно сделать, проанализировав числа и их порядок. Например, входные числа могут увеличиваться или уменьшаться с постоянным шагом или иметь какую-то другую зависимость.
После того, как мы нашли закономерность в ряде чисел, составим формулу или алгоритм, который позволит нам вычислить следующее число. Например, если у нас есть ряд чисел, увеличивающихся с шагом 2 (2, 4, 6, 8, …), то следующее число можно получить, добавив 2 к последнему известному числу.
Когда мы найдём закономерность и составим формулу или алгоритм прогнозирования, мы можем применить его для решения задачи. Например, если у нас есть ряд чисел, выражающих количество проданных билетов на концерт каждый месяц, то мы можем использовать закономерность и формулу прогнозирования для предсказания количества продаж в следующем месяце.
Прогнозирование следующего числа может быть полезным инструментом при анализе данных и решении задач. Оно позволяет нам предсказывать значения на основе имеющихся данных и выявлять тренды и зависимости. Кроме того, прогнозирование может помочь нам принимать решения и планировать будущие действия.
Типы закономерностей
Существует несколько типов закономерностей: убывающие, возрастающие, циклические и сложные закономерности. Давайте познакомимся с каждой подробнее.
Возрастающая закономерность
Закономерность, у которой числовое свойство увеличивается согласно некоторому закону или формуле, называется возрастающей.
Например, дерево растет и на его стволе каждый год добавляется одно новое кольцо. Этот процесс называется простой возрастающей закономерностью. В этой закономерности легко вычислить, сколько колец будет через 2 года или через 10 лет. Количество колец в стволе соответствует возрасту дерева.
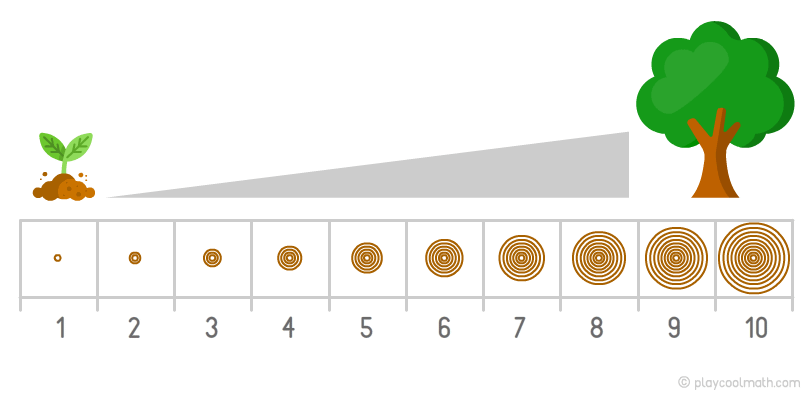
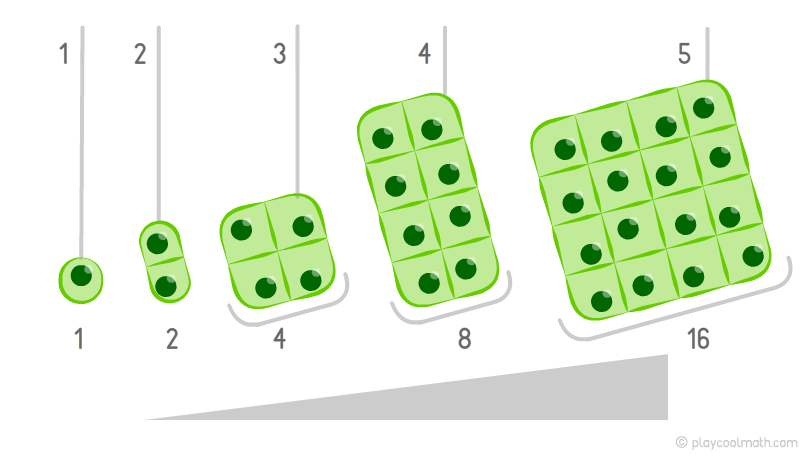
Приведем пример возрастающей закономерности, которая сложнее чем в примере с деревом. Представьте одноклеточный организм, который каждую минуту делится на две клетки. На картинке хорошо видно, что в первую минуту мы видим 1 клетку, во вторую — уже 2 клетки, а затем 4 клетки, 8, 16. Каждую минуту количество увеличивается в 2 раза. Зная предыдущее количество, можно узнать, сколько будет клеток в следующую минуту. Этот процесс называется тоже возрастающей закономерностью. Для настоящих математиков будет несложно установить формулу увеличения закономерности для этого примера. Эта задача для тебя еще сложная, так как ты только начали изучать математику. Главное сейчас чтобы ты понять, что такое закономерность.
Убывающая закономерность
Закономерность, у которой числовое свойство уменьшается согласно некоторому закону или формуле, называется убывающей.
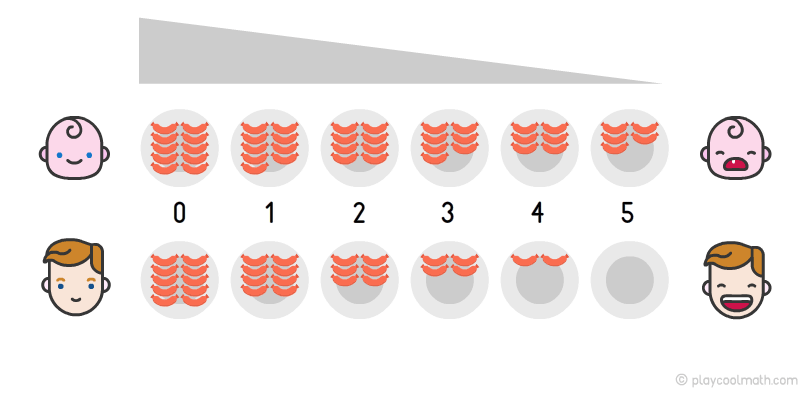
Представьте соревнования по поеданию сосисок на скорость, в которых участвуют два участника. У каждого по 10 сосисок на тарелке (это столько, сколько у тебя пальцев на руках). Первый съедает одну сосиску за минуту, а второй съедает 2 сосиски за минуту. Ясно, что второй участник соревнований победит, так как он съедает больше сосисок за минуту, чем первый участник
Но нам важно увидеть закономерность. На рисунке мы можем увидеть, как в каждой тарелке уменьшается количество сосисок
Этот процесс называется убывающей закономерностью. Второй участник съел всю тарелку сосисок за пять минут и победил!
Циклическая закономерность
Закономерность, которая повторяется каждый раз, называется циклической. Полный круг в циклической закономерности называется циклом закономерности.
Ты точно знаешь закономерность такого типа — это смена времен года. Весна-Лето-Осень-Зима и потом происходит повторение.
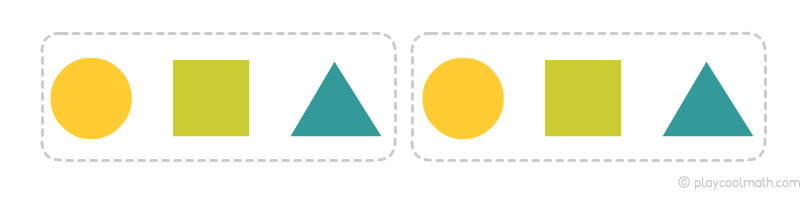
Рассмотрим пример с предметами разной формы. На рисунке ты видишь цепочку из разного количества предметов. Попробуй найти закономерность на рисунке ниже. Продолжи цепочку.

Предметы повторяются через каждые три ячейки. Зная закономерность, мы можем предположить, какие предметы будут дальше. За последним звеном будет треугольник, затем круг, далее квадрат.
Сложные закономерности
Закономерности, которые состоят из нескольких видов закономерностей или имеют несколько свойств, называются сложными.
Рассмотрим пример закономерностей на одной и той же цепочке, но будем искать закономерности в зависимости от свойства звеньев. Попробуй найти следующее звено в примере ниже.

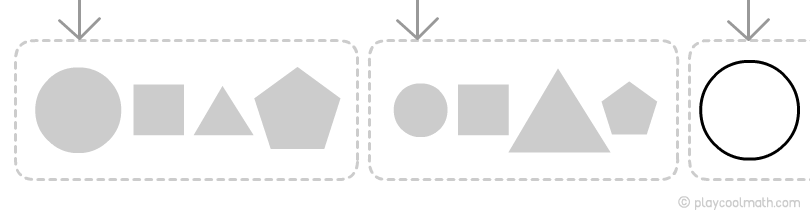
Видим, как чередуются звенья цепочки. Точно знаем, что по форме следующим будет круг, обозначим его как большой круг
Закономерность по размеру
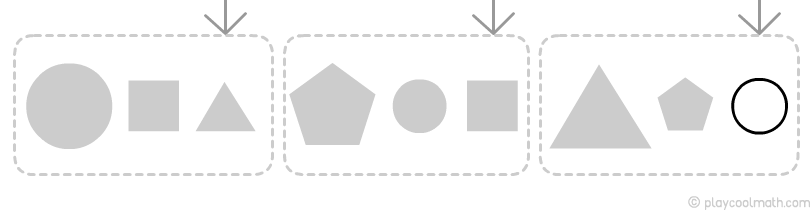
Видим, как чередуются звенья цепочки: большая и затем две маленькие фигуры, то есть следующей будет маленькая фигура.
Закономерность по цвету
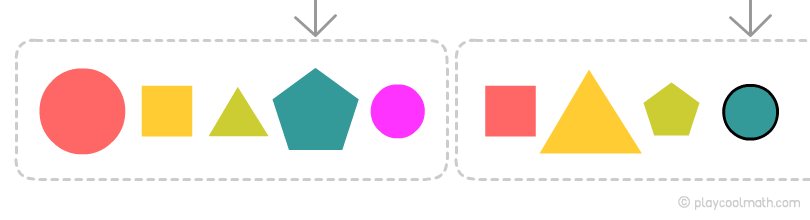
Получилась самая длинная закономерность в цепочке, выделим ее и определим, какой будет следующий цвет.
Как видишь, закономерность зависит от свойств элементов цепочки. Для одной и той же цепочки мы нашли различные закономерности в зависимости от свойства. Объединим полученные результаты и узнаем, какое звено будут следующим.

Как научить ребенка находить закономерности?
Маленьким детям, для решения задач на поиски закономерностей, понадобится только смекалка и воображение. Достаточно лишь объяснить, как можно установить закономерность между звеньями ряда. Если задачу решить не получается, то вместо прямых подсказок следует задать дополнительные вопросы, не раскрывая решение задачи полностью.
В любом случае, пользы будет больше, если ребенок решит, хотя бы одну задачу самостоятельно, нежели взрослый просто расскажет, как её решать.
Рассмотрим способы, которые помогут ребенку понять закономерности и последовательности в заданиях.
Инструкция по решению числовых последовательностей
- Найти разницу между двумя рядом стоящими числами
- Определить алгоритм построения последовательности
- Применить алгоритм к следующей паре чисел
- Использовать алгоритм для определения следующего числа в ряду
Инструкция по нахождению закономерностей в заданиях с геометрическими фигурами:
- Рассмотреть фигуры и разделить их, на повторяющиеся группы
- Определить какой элемент изменился в группе
- Решить, какая именно фигура отсутствует или является лишней.
Задания для 4 класса
Задание 1
Найди ошибку в бусах.
Решение: В первых бусах повторяются квадрат и круг, значит лишний шестой круг. Во вторых бусах, повторяется закономерность: круг, два треугольника, два круга, лишний – восьмой, по счету, круг.
Задание 2
Определите закономерность. Найдите лишнее число.
8, 16, 20, 24, 32, 40, 48, 56, 64, 72.
РешениеВ этом числовом ряду таблица умножения на 8. Ответ: число 20 – лишнее.
Задание 3
Каких геометрических фигур не хватает? Дорисуй их, соблюдая закономерность в таблице:


Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом форматеузнать подробнее
>
Задания для 2 класса
Задание 1
Найди закономерность и в пустом квадрате нарисуй нужное количество кругов.
Решение: В таблице в первом горизонтальном ряду количество кругов увеличивается на 1. Во втором ряду увеличивается на 2. Таким образом, можно предположить, что в третьем ряду количество кругов будет увеличиваться на 3 и ответ будет 9. Можно заметить, что и в вертикальных рядах эта закономерность повторяется.
Задание 2
В цепочке чисел найди закономерность и вставь пропущенные числа
95, 90, 85, 80, 75,_, 65,_, _,50
Решение: В цепочке чисел можно выделить пары: 95 -90, 85 – 80 и далее. Каждый раз, в паре, число уменьшается на 5. Значит, после 75 запишем 70, после 65 — 60, а затем 55 .
Задание 3
Найди закономерность и продолжи последовательность.
Решение: В этой цепочке чисел к каждому последующему числу прибавляется предыдущее. 2+3=5+3=8+5=13+8=21+13=34 и далее.
Задание 4
В поезде едут геометрические фигуры. Нарисуйте фигуры, в четвёртом вагоне, соблюдая закономерность их расположения.
Решение: В поезде едут геометрические фигуры: квадрат, треугольник, прямоугольник и круг. В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.
Что такое закономерность в математике?
Математическая закономерность – это определенное правило, по которому в числовом, фигурном или другом ряду элементов происходит повторение или изменение самих элементов или их свойств в соответствии с заданным правилом.
Из учебных материалов с картинками и видео, подготовленных опытными педагогами, ваш ребёнок узнает:
- что собой представляют закономерности, каких видов они бывают (циклические, возрастающие и убывающие);
- с чего начать решение задачи и как понять, в каких направлениях думать;
- как строятся умозаключения о том, какое число, буква или фигура должны продолжить предложенный ряд.
Рекомендуем взрослым и детям сначала решить несколько заданий вместе. Продолжить занятия ребёнок может самостоятельно.
В курсе развития мышления LogicLike
Пройдите 3 главы-разминки и откройте доступ к закономерностям и другим занимательным заданиям на логику.
Для ознакомления с темой предлагаем несколько примеров заданий по математике на поиск закономерностей разного уровня сложности.
Задачи для 1 класса
Найди закономерность и продолжи числовой ряд:
Картинки расставили в определённом порядке (в виде закономерности). Подумай, какой элемент будет следующим.
Догадайся, как нужно раскрасить последние 3 карандаша, чтобы сохранить закономерность в этом ряду:
Примеры заданий для 2-3 классов
Фигуры разложили в виде закономерности (в определённом порядке). Продолжи закономерность: выбери подходящий набор фигур.
Какую закономерность можно заметить? Продолжи ряд чисел:
Помоги Алисе найти числовую закономерность и запиши следующие два числа, которые ее продолжат:
Задача повышенной сложности (математика 4 класс)
Ученики посадили дерево. Его высота составляла 72 см. Через год дерево выросло до 80 см, через 2 года — до 86 см, через 3 года — до 90 см.
Какой высоты (в см) будет деревце через 9 лет, если закономерность его роста не изменится?
Задания для 1 класса
Задание 1
Раскрась дорожки для зайчика и белочки, сохраняя закономерность.
Решение: Белочка и зайчик бегут по разным дорожкам. У каждой дорожки есть своя закономерность. У зайчика повторяется 3 цвета на дорожке: красный, голубой, жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый, жёлтый.
В этом задании можно обратить внимание на то, что обе дорожки состоят из 12 кругов. Но количество повторяющихся цветов разное
Задание 2
Найди закономерность в ряду геометрических фигур.
Решение: В этом ряду нужно обратить внимание на размеры фигур, а не на цвет и форму. Сначала идет одна большая фигура, а за ней две маленькие, далее они повторяются
Задание 3
Нарисуйте в четвертом квадрате правильный ответ.
Решение: Рассмотрев внимательно рисунок, мы увидим, что круги в квадратах исчезают по одному, против часовой стрелки. В этой задаче имеет значение только расположение кругов квадрате. Таким образом, в последний квадрат мы должны нарисовать один синий круг в нижнем левом углу.
Задание 4
Соблюдая закономерность, продолжи ряд чисел до 10. Сформулируй правило, которое действует в этой закономерности. Используя это правило, придумай свою закономерность.
Решение: В этом ряду каждая цифра увеличивается на 2 относительно предыдущей – мы вычислили правило для данной закономерности. Значит, чтобы продолжить ряд, мы прибавим к каждой следующей цифре по 2. Ответ будет выглядеть так: 2,4,6,8,10.
Чтобы придумать подобную закономерность, нужно использовать сформулированное выше правило: например, 1,3,5,7,9.
Как научить детей находить закономерности?
Объясните понятие закономерности и покажите на конкретных примерах несколько типов последовательностей. Поясните, как вы рассуждаете, чтобы найти закономерность между числами, буквами, картинками, любыми элементами ряда.
Пособие по математике для детей дошкольного возраста.
Цель: Учить детей совершать мыслительные операции: продолжать ряды геометрических фигур по образцу; закреплять знания геометрических фигур.
Я изготовила математические карточки и большое количество плоскостных геометрических фигур разных цветов, которые дети могут использовать для продолжения ряда.
На карточках изображены геометрические ряды, которые не повторяются. Дети должны выбрать карточку, внимательно рассмотреть нарисованный на ней ряд фигур и продолжить его, используя раздаточный материал.
Дети с удовольствием играют
Для создания игры я использовала цветной и белый картон. Белый картон разделила на две части, на каждой из частей нарисовала линии. Геометрические фигуры вырезала из цветного картона. На линии наклеила геометрические фигуры (начала ряд).
-
Технологическая оснащенность производства конспект
-
Гражданское общество местное самоуправление 9 класс конспект урока
-
Конспект опера орфей и эвридика 3 класс критская
-
Конспект урока по изо с презентацией
- Увеличение на несколько единиц прямая форма конспект урока






























