Виды геометрических тел и их характеристики

Простейшие следствия из аксиом стереометрии

На основе аксиом можно доказать несколько простых теорем стереометрии.

Доказательство. Возьмем произвольную прямую m и точку C, которая НЕ принадлежит m. Далее отметим на m две любые точки и обозначим их как А и В:

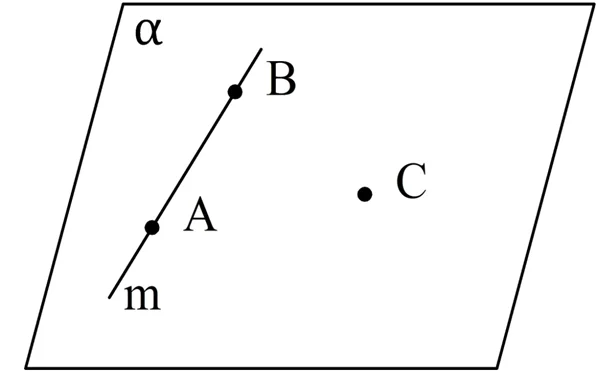
По аксиоме 1 через А, В, С можно провести некоторую плос-ть α. По аксиоме 4 прямая m будет принадлежать α. Тем самым мы показали, что существует плос-ть, проходящая через m и C. Единственность этой плос-ти вытекает уже из аксиомы 2, ведь через А, В и С нельзя провести две различных плос-ти, ч. т. д.

Иногда доказанный факт формулируют иначе: прямая и точка, не находящаяся на прямой, однозначно определяют проходящую через них плос-ть. То есть, указав прямую и точку, можно одновременно указать на ту плос-ть, которая задается ими.

Переходим к следующей теореме.

Отметим на произвольной прямой m точки А и В. Далее выберем ещё две точки в пространстве C и D, причем такие, что А, В, С и D не находятся в одной плос-ти. Тогда у нас есть плос-ти АВС и АВD, которые пересекаются по прямой АВ:

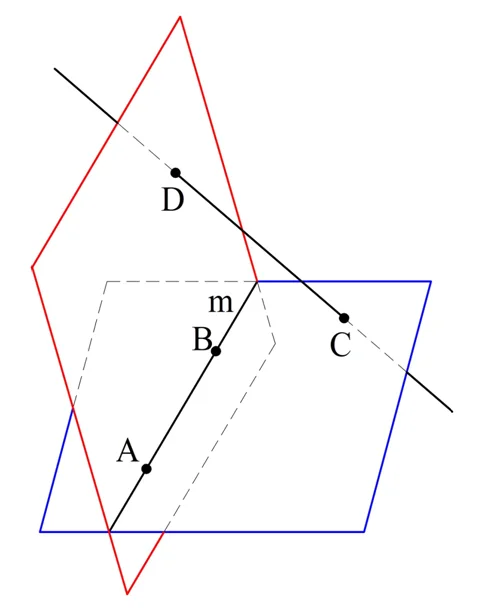
Теперь соединим С и D прямой. Прямая CD состоит из бесконечного количества точек. Через каждую из них можно провести единственную плос-ть, которая будет проходить через АВ. Так как точек бесконечно много, то и плос-тей будет бесконечно много. Осталось лишь показать, что никакие две таких плос-ти не будут совпадать, то есть все они различны.

Действительно, пусть две таких плос-ти совпадают, то есть на самом деле являются одной плос-тью. Тогда получается, что эта единая плоскость проходит через две точки прямой СD. Тогда, по аксиоме 4, вся прямая СD принадлежит этой плос-ти, в том числе и сами точки С и D. Но плос-ть проходит также через А и В. То есть получится, что А, В, С и D входят в состав одной плос-ти, а это не так. Это противоречие означает, что на самом деле все плоскости, проходящие через разные точки прямой CD, будут различны, ч. т. д.

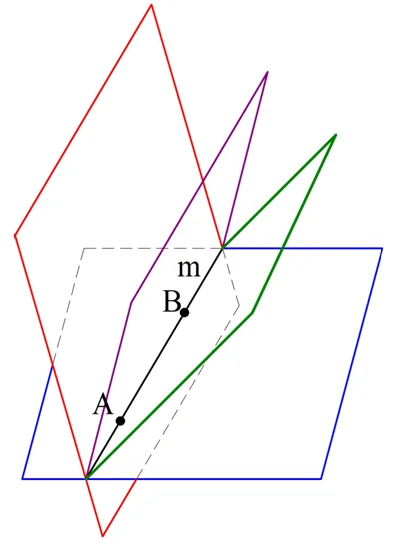
Рассмотрим ещё одну теорему:

Пусть пересекаются прямые m и n. Обозначим точку их пересечения как А. Также выберем на m некоторую точку В, а на n – точку C. Мы можем построить плос-ть α через точки А, В и C, и она будет единственной. Так как и А, и В принадлежат α, то и вся прямая m ей принадлежит (аксиома 4). Аналогично и прямая n находится на плос-ти α. То есть α как раз и является плос-тью, о которой говорится в теореме. Никакая другая плос-ть не будет содержать обе прямые m и n, ведь в противном случае она проходила бы через точки А, В и С, то есть совпадала бы с α.

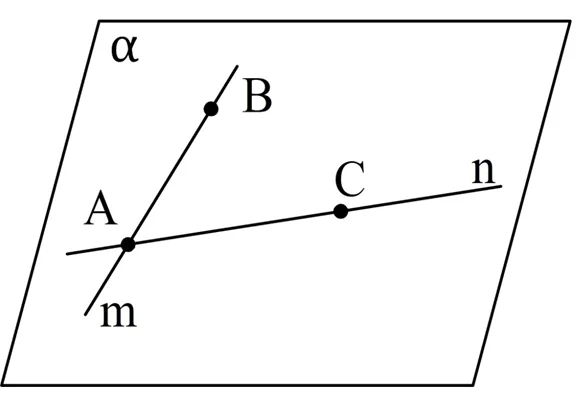
Эта теорема также говорит о том, что две пересекающиеся прямые однозначно определяют проходящую через них плос-ть.

Развертка четырехугольной пирамиды

Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра – треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.

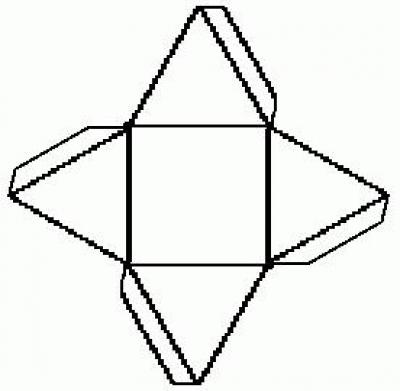
Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.

Сходящиеся и параллельные линии

Вы можете использовать множество различных стилей и форм, чтобы создать что-то свое. Например, можно использовать фигуры, создающие иллюзию отражения, как в данном случае. Различные эффекты и иллюзии могут быть достигнуты путем сочетания различных форм, освещения и цветов, и есть много материала, с которым можно работать.

Если вы хотите добавить больше смысла в свою фотографическую работу, чтобы усилить эмоциональное воздействие на зрителя, то вам следует попытаться понять, как понимается пространство. В некоторых случаях фотография на первый взгляд может показаться довольно простой. Например, эти. Что здесь самое главное? Правильно. Близость зрителя к скамейке, указанной автором, и наличие пространства, вернее, пустоты, сразу за ней. Такая синтетическая конструкция кадра позволяет зрителю реконструировать историю сюжета в собственном сознании и подсознании, основываясь на собственном опыте, собственных чувствах и эмоциях.

Определение геометрического тела

Такие понятия, как луч, отрезок, ломаная, кривая встречаются довольно часто в различных науках: математике, алгебре, физике и химии (траектория движения, графики и т.д.).

Все перечисленные фигуры можно представить как множество точек.

Любую фигуру в геометрии можно представить как множество точек, сгруппированных определенным образом.

Разберем понятие геометрического тела.

Представленный выше вариант определения геометрических тел не единственный. Иногда используют следующее определение: геометрическое тело — множество сгруппированных точек, из которых две любые точки образуют отрезок, не выходящий за границы тела.

Упражнения геометрические фигуры

Выполните следующие задания на тему «Геометрические фигуры для детей»:

1. Найди спрятанные геометрические фигуры на рисунке.
2. Подбери нужную форму к каждой геометрической фигуре.
3. Попробуйте составить геметрическую фигуру из счетных палочек.
4. Обведи по точкам геометрические фигуры, и раскрась их.
5. Вырежи геометрические фигуры и наклей в нужные места.
6. Продолжи ряд геометрических фигур.
7. Начерти геометрические фигуры в порядке возрастания по размеру.
8. Попросите ребенка нарисовать в определенной последовательности следующие фигуры: круг, трапеция, овал, ромб, квадрат.
9. Какие геометрические фигуры напоминают предметы: пирамидка, мяч, шар, холодильник, книга?
10. Используя геометрические фигуры составть по образцу рисунок.
11. Сколько геометрических фигур изображено на картинке?
12. Какая фигура пропущена в таблице? Впиши недостающую геометрическую фигуру.
13. Нарисуй геометрические фигуры и раскрась в разные цвета.
14. Нарисуй геометрические фигуры круги, треугольники и квадраты разных размеров.
15. Определи в какой последовательности распологаются геометрические фигуры, продолжи ряд.
16. Назови фигуры в которых есть острые углы.
17. Зачеркни лишнюю фигуру в каждом ряду.
18. Геометрические фигуры разделенные на части, собери их в целую фигуру.
19. Запомни и повтори геометрические фигуры, которые были изображены на рисунке.
20. Раскрась фигуры из которых можно составить треугольник.
21. Определи из каких геометрических фигур состоит рисунок.
22. Продолжи последовательность геометрических фигур.
23. Нарисуйте рисунок из геометрических фигур.

После выполнения разнообразных заданий на тему геометрические фигуры у ребенка:

• Сформируется представление о геометрических фигурах.
• Сможет легко найти геометрические фигуры в пространстве и на листе.
• Будет знать названия каждой фигуры и отличать ее от других геометрических фигур.

Геометрические фигуры и их названия:

• Круг
• Квадрат
• Треугольник
• Прямоугольник
• Трапеция
• Ромб
• Параллелограм
• Пятиугольник
• Шестиугольник
• Семиугольник
• Восьмиугольник
• Девятиугольник
• Десятиугольник

Подготовьте для занятия пять геометрических фигур и попросите ребенка определить какую геометрическую фигуру он взял в руки.

Расставьте перед ребенком четыре геометрические фигуры. Попросите ребенка запомнить расположенные фигуры на столе. Закройте плотным листом бумаги геометрические фигуры и уберите 1 из них. Затем попросите ребенка назвать ту геометрическую фигуру, которая исчезла.

Выложите в ряд четыре геометрические фигуры и попросите ребенка запомнить их расположение. Закройте плотным листом бумаги данный ряд геометрических фигур, а затем две фигуры поменяйте местами друг с другом. Спросите у ребенка, что изменилось в расположении геометрических фигур и попросте вернуть их в прежнее месторасположение.

С геометрическими фигурами можно придумать игру судоку и усложнять ее уровни при дальнейшей игре.

Какая фигура лишняя?

Найди лишнюю фигуру и объясни почему именно выбранная фигура является лишней.

Зачеркни лишнюю фигуру.

Запиши номер лишней фигуры.

Запишите какие фигуры изображены на рисунке.

Выберите лишнюю фигуру.

Часть какой фигуры изображена на рисунке.

Вместо заключения

Очень часто процесс обучения ребенка геометрическим фигурам (да и не только фигурам) воспринимается родителями исключительно как постоянное экзаменирование ребенка, т.е. они пару раз показывают ребенку, например, квадрат, а в дальнейшем же обучение сводится к вопросу «Скажи, какая это фигура?». Такой подход крайне неправильный. Во-первых, потому что как и любой человек, ребенок не слишком любит, когда ему устраивают проверку знаний, и это только отбивает у него охоту заниматься. Во-вторых, прежде чем о чем-то спрашивать малыша, ему нужно очень много раз это объяснить и показать!

Поэтому постарайтесь сводить проверочные вопросы к минимуму. Просто повторяйте и повторяйте изучаемую информацию, будь то названия фигур или чего-то еще. Делайте это во время игр и бесед с малышом. А то, что ребенок все усвоил, вы вскоре и сами увидите без лишних проверок.

Основные геометрические фигуры

Косновным геометрическим фигурам
на плоскости относятсяточка
и прямая линия
.Отрезок
,луч
,ломаная линия
— простейшие геометрические фигуры на плоскости.

Точка
—
это самая малаягеометрическая фигура
, которая является основой всех прочих построений (фигур) в любом изображении или чертеже.

Всякая более сложная геометрическая фигура — это множествоточек
, которые обладают определенным свойством, характерным только для этой фигуры.

Прямую линию
, или прямую, можно представить себе как бесчисленное множествоточек
, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:

Частьпрямой линии
, ограниченная с двух сторонточками
, называется отрезком прямой, или отрезком
. Отрезок изображается так:

Луч
— это направленная полупрямая, которая имеетточку
начала и не имеет конца. Луч изображается так:

Если напрямой
вы поставилиточку
, то этой точкой прямая разбивается па двалуча
, противоположно направленных. Такиелучи
называются дополнительными.

Ломаная линия
— это несколькоотрезков
, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общуюточку
) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.

Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой. Примером замкнутой ломаной служит любой многоугольник:

Трехзвенная замкнутая ломаная линия — треугольник

Плоскость
,
как и прямая, — это первичное понятие, не имеющее определения. У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.

Одновременно с изучением цветов, ребенку можно начать показывать карточки геометрические фигуры. На нашем сайте Вы сможете скачать их бесплатно.

Как изучить с ребенком фигуры по карточкам Домана.

1) Начинать нужно с простых фигур: круг, квадрат, треугольник, звезда, прямоугольник. По мере освоения материала, начинать изучать фигуры посложнее: овал, трапеция, параллелограмм и т.д.

2) Заниматься с ребенком по карточкам Домана нужно несколько раз в день. При демонстрации геометрической фигуры четко проговаривайте название фигуры. А если во время занятий вы будете еще пользоваться наглядными предметами, например, собирать вкладыши с фигурами или игрушку — сортер, то малыш очень быстро освоит материал.

3) Когда ребенок запомнит название фигур, можете переходить к более сложным заданиям: теперь показывая карточку говорите — это синий квадрат, у него 4 равные стороны. Задавайте ребенку вопросы, просите его самого описать, что он видит на карточке и т.д.

Такие занятия очень полезны для развития памяти и речи ребенка.

Занятия по карточкам Домана

прекрасно развивают зрительную память, внимательность, речь ребенка. Это отличная зарядка для ума.

Понятие светотени

Любой объект ограничен прямолинейными либо криволинейными плоскостями. Каждая из них во время освещения попадает в особые световые и цветовые условия – одни участки освещаются сильнее, другие – слабее. На интенсивность освещенности также влияет расстояние до источника света и угол падения потока света на поверхность объекта. Самыми освещенными будут те участки, на которые световые лучи падают под прямым углом, и наоборот, чем больше наклон потока света, тем темнее поверхность. Светлота также зависит от фактуры и цвета. Например, полированные материалы отражают свет лучше, матовых и шероховатых, а чем темнее участки, тем сильнее поглощается свет.

Наряду с геометрией объекта, градация света и тени является важной составляющей передачи объема. Чтобы создать иллюзию объемного предмета, необходимо правильно изобразить светотень, состоящую из:

• блика;
• света;
• падающей и собственной тени;
• полутона;
• рефлекса.

Блик – самая яркая часть светотеневого рисунка, где световой поток практически полностью отражается. Свет – наиболее освещенная часть предмета, а собственная тень – самая темная. Промежуточная по светлоте и месторасположению область называется полутенью или полутоном, а рефлекс – это отраженный в теневой части предмета свет. Отражение дают любые, находящиеся со стороны тени объекты: стены, потолок, поверхность стола и т. п. Падающая тень – это та, которую отбрасывает предмет на окружающие его поверхности.

На приведенном выше рисунке светотень изображена с помощью штриховки – классического метода, которому обучают в художественных школах. Однако штриховка не является естественной для глаза формой передачи объема, поэтому на наших занятиях по рисунку мы ее заменяем тонированием с помощью графитового порошка. Работа ведется «от пятна», линии и переходы получаются мягкими и естественными. Подробности смотрите в видео

Очень важно определить границу между светом и тенью. У начинающих художников с этим обычно возникают трудности, потому что пограничная зона всегда разная и зависит от условий освещения

Например, на шаре она изогнутая, на цилиндре – прямая, на вазе – извилистая, а на портрете имеет сложную конфигурацию.

Основные геометрические фигуры

Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости. 

Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.

А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.

Разберём плоские фигуры.

Треугольник

Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.

 Есть три вида треугольников:

• Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.
• Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.
• Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.

Треугольники имеют следующие свойства:

• в треугольнике напротив большего угла лежит большая сторона и наоборот;
• сумма углов треугольника всегда равна 180 градусам;
• все углы равностороннего треугольника равны 60 градусам;
• в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).

Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.

Примеры треугольников:

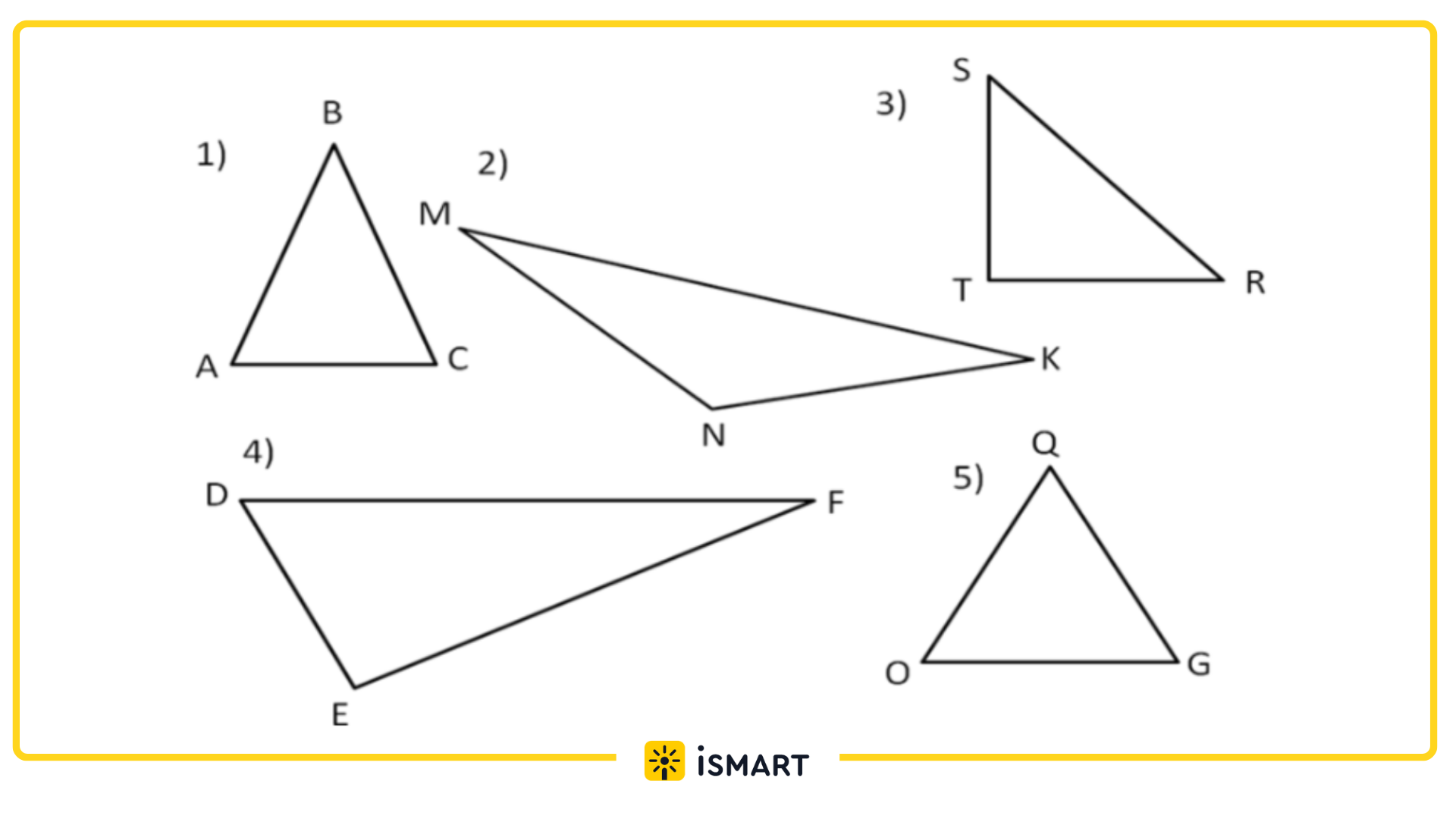
Окружность

Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии. 

Круг

Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.

Прямоугольник

‍Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:

• противоположные стороны равны между собой;
• диагонали равны и делятся в точке пересечения пополам;
• около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.

Квадрат

Квадрат — это тот же прямоугольник, у которого:

• все стороны равны;
• все углы равны и составляют 90 градусов;
• диагонали равны и перпендикулярны;
• центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.

Трапеция

Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность. 

Параллелограмм и ромб

Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм с равными сторонами.

Параллелограмм имеет следующие свойства:

• противоположные стороны и углы равны;
• сумма двух любых соседних углов равна 180 градусам;
• диагонали пересекаются и точкой пересечения делятся пополам;
• каждая диагональ делит фигуру на два равных треугольника.

Средняя группа

Предлагаем дидактические игры для детей «Геометрические фигуры», которые можно использовать в средней возрастной группе, то есть для воспитанников 4-5 лет.

Чудесный мешок

Возьмите для игры среднего размера мешок из непрозрачного материала, подберите несколько некрупных предметов, имеющих четко определяемую геометрическую форму: мяч, клубок ниток, яблоко, коробку с карандашами, кубик, коробок спичек и прочее. Положите все в мешок, попросите ребенка вытянуть предметы только круглой формы, затем только прямоугольной.

Геометрический футбол

Игра знакомит дошкольников с двумя пространственными объектами: шаром и кубом. Соорудите на столе подобие футбольных ворот. Попросите ребенка закатить в ворота сначала шар, затем куб. Затем помогите воспитаннику сделать выводы: шар не имеет углов, поэтому легко перекатывается, куб сдвинуть с места сложнее из-за наличия граней, зато он устойчивее на горизонтальной поверхности.

Домик для ежа

Для игры вырежьте треугольники разного размера: возьмите два бумажных квадрата – один большего размера, второй меньшего, разрежьте их диагонально. Разложите получившиеся фигуры перед воспитанником, расскажите, что наступила осень, ежик готовится уснуть до весны, нужно помочь ему соорудить уютный домик из всех представленных треугольников.

Рыбка

Вырежьте из квадратных листов треугольники по вышеописанному методу. Попросите дошкольника составить из фигур рыбку. Это можно сделать несколькими способами, главное – треугольники не должны пересекаться. Если какой-то вариант геометрической рыбки понравится ребенку больше остальных, из него можно сделать с помощью клея аппликацию.

Эстафета

Разделите воспитанников на две команды. Каждая группа детей становится в ряд. В начале каждого ряда поставьте табурет. На другом конце помещения положите на стол перемешанные меж собой картонные квадраты и треугольники.

Когда прозвучит старт, игроки по очереди подбегают к столу, хватают фигуру, несут ее к своему табурету. Первая команда должна собирать квадраты, вторая – треугольники. Игра завершается, когда в одной из команд в эстафете поучаствуют все игроки. Эта команда и побеждает, но при условии, что фигуры собраны правильно.

Скажи одним словом

Для игры подготовьте группы геометрических фигур, объединенных формой, но с разными остальными признаками. Например, крупные и маленькие прямоугольники, круги разных цветов. Раскладывайте объекты на столе по 4 штуки. Ребенок должен назвать их обобщающим словом.

Разложи по размеру

Для игры сделайте парные геометрические фигуры: один объект в паре крупный, второй маленький. Положите на стол два квадрата. Задача воспитанника – положить на квадраты остальные объекты соответственно их размеру. То есть на крупный квадрат нужно класть большие треугольники, овалы и прочее, а на маленький – такие же маленькие.

Дидактическая игра «Найди фигуры»

Для настольной игры сделайте парные карточки, изображающие несколько геометрических форм. Одни картинки из пар заберите, вторые разложите на столе. Демонстрируйте детям карточки по очереди, а они должны отыскать на столе аналогичные изображения.

Найди домик

Для подвижной игры раздайте детям по маленькому геометрическому изображению: одним круг, другим квадрат, третьим треугольник и так далее. Расставьте в разных местах игровой комнаты табуреты с изображением соответствующих форм. Включите музыку, под которую дети должны бегать по помещению, танцевать. Когда музыка прервется, дети должны быстро отыскать свой «домик», то есть табурет, подбежать к нему. Игру можно усложнять: отодвигать табуреты так, чтобы игроки этого не заметили.

Дидактическая игра «Фигуры и формы»

Для игры распечатайте геометрические картинки. Показывайте ребенку фигуры вразнобой, а он должен назвать объект соответствующей формы. Например, увидев круг, воспитанник может назвать следующие предметы: яблоко, мяч, апельсин, колесо, солнце.

Что спрятано

Разложите перед воспитанником геометрические изображения. Пусть дошкольник внимательно на них посмотрит, затем закроет глаза, не подглядывает. Спрячьте одну из картинок. Воспитанник, открыв глаза, должен вспомнить, какая фигура исчезла.

Виды геометрических тел и их характеристики

Все геометрические тела можно разделить на два типа:

• многогранники;
• тела вращения.

Характеристиками многогранников и тел вращения считают их объем и площадь поверхности.

Среди многогранников выделяют правильные многогранники, образованные правильными равными многоугольниками. К правильным можно отнести тетраэдр, гексаэдр, октаэдр.

Основными элементами многогранника являются:

1. Грань — поверхность, ограничивающая многогранник.
2. Ребро — линия пересечения двух соседних граней.
3. Вершина — точка, в которой пересекаются два или более ребра.

Приведем формулы для расчета объема некоторых многогранников.

Площадь поверхности многогранника находят как сумму площадей его граней.

Прямая призма.

Параллелепипед и его частный случай — куб.

Пирамида.

Основной элемент любого тела вращения — ось — прямая, вокруг которой происходит вращение плоской фигуры, образующей тело.

У конусов и цилиндров выделяют также такой элемент как образующая.

Множество всех образующих конуса или цилиндра называют образующей или боковой поверхностью.

Приведем формулы для вычисления основных характеристик тел вращения — объема V и площади поверхности S.

Шар.

Конус.

Цилиндр.

Схемы для вырезания

Учащиеся 1-2 классов знакомятся с простыми геометрическими фигурами и трехмерными фигурами в школе: Квадрат, куб, прямоугольник. Их несложно резать и клеить. Узоры развивают мелкую моторику детей и дают им первые представления о геометрии.

Учащиеся средних классов, работающие по шаблону, делают из бумаги сложные фигуры: шестиугольники, пятиугольники и цилиндры. Дети делают из бумаги кукольные домики, мебель, оригами, замок для маленьких игрушек, маски для лица (трехмерные называются многоугольными).

Овала

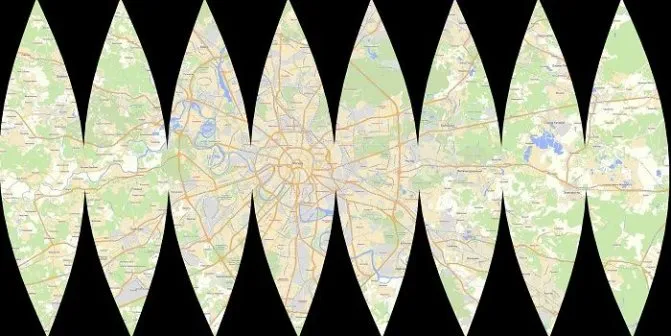
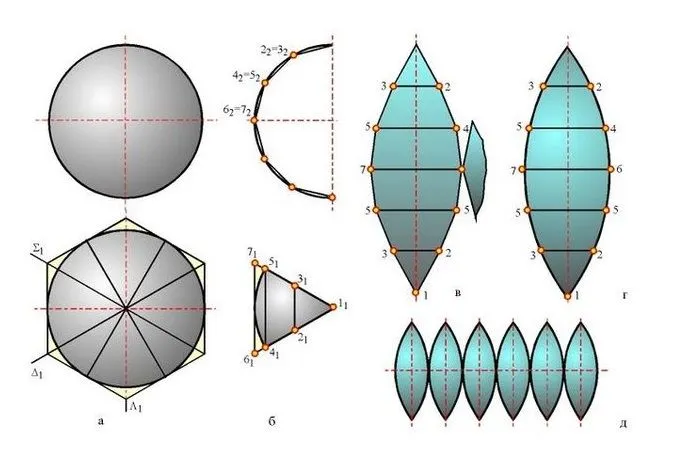
Узор из шаров состоит из 8, 12, 16 или более деталей. Существуют и другие способы изобразить мяч. Например, из 6 частей или 4 широких клиньев.

В качестве материала для изготовления плотного шара можно использовать картон или плотную бумагу.