Что такое экспонента

В IT-культуре

Число e является предметом многочисленных похвал в ИТ-сообществе.

Для IPO в 2004 году объявила, что хочет привлечь не круглую цифру, как это обычно бывает, а 2 718 281 828  долларов , или е миллиарда долларов (с точностью до доллара). Google также стоит за оригинальной кампанией по набору персонала в июле 2004 года: знаки с упоминанием «{первое 10-значное простое число в последовательных цифрах e} .com» ({первое 10-значное простое число в последовательных десятичных разрядах e} .com ), выставленный сначала в Кремниевой долине , затем в Кембридже , Сиэтле и Остине, побудил любопытных посетить сайт, ныне несуществующий 7427466391.com. Там посетитель должен был решить еще более сложную задачу, которая, в свою очередь, направила его на сайт Google Labs, где его пригласили отправить резюме. Первое десятизначное простое число в десятичной системе e — это 7427466391, которое начинается с 99- го  десятичного знака.

Компьютерный ученый Дональд Кнут пронумеровал различные версии своей программы Metafont в соответствии с десятичными знаками e  : 2, 2,7, 2,71, 2,718 и так далее. Точно так же номера версий его программы TeX приближаются к π .

Число е как предел

Первым число е неожиданно вычислил швейцарский математик Якоб Бернулли, решая задачу, никак не связанную с логарифмами. В 1690 году он опубликовал исследование так называемого сложного процента — дохода, составляющего определённый процент (р — процентная ставка, доля) от предоставляемой суммы денежных средств. При каждом очередном его вычислении учитывается исходная сумма вместе с начисленными ранее процентами. Таким образом, исходная сумма S после n начислений превращается в

S = (1 + p)n · S.

Например, при годовой процентной ставке 100% (р = 1) исходная сумма по истечении года (n = 1) удваивается, и каждый рубль превращается в два. Но что будет с полученным доходом, если начислять процент чаще, но во столько же раз уменьшать процентную ставку? Например, если каждые полгода начислять по 50% (р = 0,5), то в конце года у вас вместо 1 рубля будет:

S = (1 + ½)2 · 1 руб. = 2,25 руб.

А если начислять каждый месяц, то

S = (1 + 1/12)12 · 1 руб. = 2,261303… руб.

Бернулли показал, что если частоту начисления процентов увеличивать бесконечно, то величина (1 + 1/n)n имеет предел, лежащий между 2,5 и 3. Это была первая грубая оценка числа е. Бернулли не представлял всей значимости полученного им результата, а потому не стал проводить длительные трудоёмкие вычисления, определяя это значение более точно. Он даже не дал ему никакого обозначения. А ведь именно этот предел теперь служит в математике определением числа е. В со-временных обозначениях:

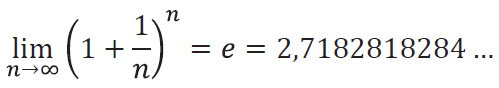
Именно такую сумму даст 1 рубль за год, если начислять процент непрерывно.

Имя Якоба Бернулли также связано с натуральным логарифмом и числом e через изученные им свойства различных кривых. Правда, их связи с найденным пределом он не увидел, возможно, просто не успел, поскольку скончался в возрасте 50 лет. Любимым объектом изучения Бернулли стала так называемая логарифмическая спираль, современная формула которой записывается как ln r = kθ или r = aebθ, где a, b и k — константы. Именно Бернулли первым начал широко использовать при построении кривых полярные координаты (в них положение точки на плоскости описывается двумя числами: радиусом r и углом θ).

В отличие от спирали Архимеда, где витки идут через одинаковое расстояние, витки логарифмической спирали расходятся (расстояние между ними увеличивается). Она часто встречается в природе, её можно обнаружить в строении живых организмов, ураганов и даже галактик. Нашла логарифмическая спираль своё место и в искусстве как способ построения орнаментов и композиций. Так, великий художник эпохи Возрождения Альбрехт Дюрер посвятил ей труд, где показывал, как строить и применять спираль для вычерчивания волют (завитков) капителей, побегов с листвой или украшений епископского жезла.

Рукава галактики M 51 в созвездии Гончие Псы представляют собой логарифмическую спираль. Иллюстрация: NASA/ESA/S. Beckwith (STScI)/Hubble Heritage Team (STScI/AURA)Разрез раковины головоногого моллюска наутилуса, показывающий камеры, расположенные приблизительно по логарифмической спирали (пунктирная синяя кривая). Иллюстрация: Dicklyon/Wikimedia Commons/CC BY-SA 4.0Арка в форме цепной линии в шахском дворце Сасанидов Таки-Кисра (не позднее III века до н. э.) в одном из крупнейших городов античности Ктесифоне (в 32 км от современного Багдада, Ирак). Фото: Library of Congress’s Prints and Photographs/PD

Сейчас даже трудно представить, с какими сложностями сталкивались исследователи того времени, не имея в своём распоряжении современных форм математической записи и средств математического анализа. Задачи, которые в наше время за считаные минуты решит студент-первокурсник, требовали от них месяцев напряжённой работы и совершения открытий.

Логарифмическая спираль настолько восхитила Бернулли своими свойствами, что он называл её «spira mirabilis» — «удивительная спираль» и даже завещал выбить её на своём надгробии вместе с надписью «EADEM MUTATA RESURGO» («изменённая, я возрождаюсь такой же»), которая описывает свойство этой кривой сохранять свою форму после некоторых преобразований. Правда, тут история немного пошутила над математиком, необразованный мастер изобразил на надгробии спираль Архимеда…

Применения числа е

Исходя из полученного равенства

можно доказать, что

где — любая бесконечно малая величина, могущая принимать и положительные и отрицательные значения.

Последнее равенство можно сформулировать так:

Степень, основанием которой служит единица плюс бесконечно малое слагаемое 7, а показателем величина, обратная этому слагаемому, стремится к числу е, как к своему, пределу (доказательство опускается).

Обратим внимание на то, что основание этой степени стремится к единице, но, несмотря на это, сама степень не стремится к единице. Рассмотрим пределы степеней, в которых основанием служит единица плюс бесконечно малое слагаемое, а показатель есть величина, обратная этому слагаемому

Рассмотрим пределы степеней, в которых основанием служит единица плюс бесконечно малое слагаемое, а показатель есть величина, обратная этому слагаемому.

Примеры:

1. Найти

Решение:

Полагая получим При Следовательно,

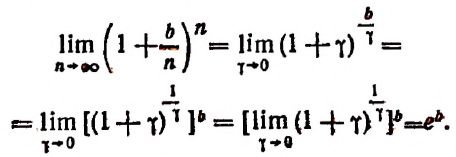
2. Найти

Полагая получим Следовательно,

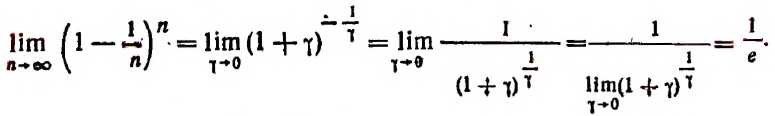
3. Найти

Полагая получим Следовательно,

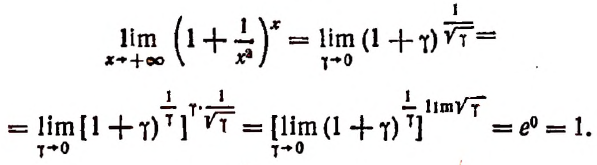
4. Найти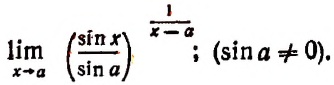

Представим в виде суммы, у которой первое слагаемое было бы единицей, а второе — величиной бесконечно малой. Это легко сделать.

Действительно,

Здесь первое слагаемое есть единица, а второе, стоящее в скобках, есть величина бесконечно малая при

Таким образом, получим:

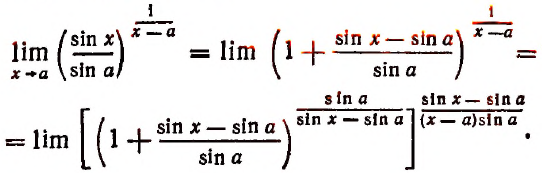
В квадратных скобках мы имеем степень, основанием которой является единица плюс бесконечно малое слагаемое, а показатель степени есть величина, обратная этому бесконечно малому слагаемому. Предел такой степени, как мы знаем, равен числу е.

Теперь найдем предел показателя степени, в который возводится выражение, стоящее в квадратных скобках:

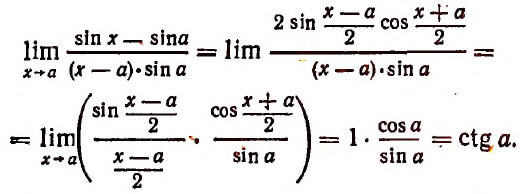
Следовательно,

Задачи:

1. Пусть банк принял вклад в a руб. и обязался присоединять процентные деньги к вкладу через каждую часть года из расчета р годовых процентов. Спрашивается, в какую сумму обратится первоначальный вклад через t лет?

Одну n-ю часть года назовем установленным промежутком времени. Тогда один год будет содержать n, a t лет nt таких промежутков.

К концу первого промежутка времени вклад обратится в

Действительно, за первый промежуток времени процентные деньги, подлежащие присоединению к вкладу, будут равны Следовательно, вклад окажется равным т. е.

Обратим внимание на то, что для получения возросшей суммы за один промежуток времени достаточно вклад, имевшийся в начале промежутка, умножить на Этот множитель называется множителем процентного наращения за промежуток времени, равный части года. Значит, чтобы получить возросшую сумму к концу второго промежутка времени, достаточно вклад, образовавшийся к началу второго промежутка времени, умножить на множитель процентного наращения и т

д

Значит, чтобы получить возросшую сумму к концу второго промежутка времени, достаточно вклад, образовавшийся к началу второго промежутка времени, умножить на множитель процентного наращения и т. д.

Таким образом,

Итак, первоначальный вклад в а руб. обратится через t лет в

Теперь вообразим, что т. е. что рост вклада происходит, как выражаются, органически. Тогда вклад в а руб. обратится через t лет в сумму А, определяемую равенством

Полагая найдем, что

Отсюда

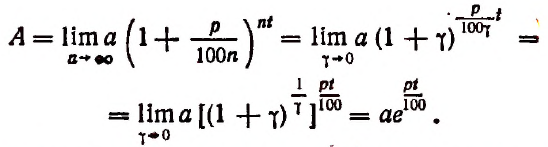
Итак, для органического роста вклада получилась следующая формула:

Например, при а = 1, р = 5 и f = 100

т. е. один рубль превращается через 100 лет приблизительно в 143 руб., если органический рост происходит по 5 годовых процентов.

2. Лесная делянка содержит в данный момент а куб. м древесины. Сколько окажется на этой делянке древесины через t лет, если органический рост древесины происходит по р годовых процентов.

Oтв. куб. м.

3. Численность населения города увеличивается ежегодно на р% (по отношению к началу года). Через сколько лет численность населения удвоится?

Отв.

Приглядимся поближе

Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение?

Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

В следующий статье мы посмотрим на пример экспоненциального роста ваших денег.

Переопределение экспоненциальным

Отношение к основанию натурального логарифма

Эйлер видел в экспоненциальных функциях и функциях логарифма взаимные функции друг друга. Записывая эквивалентность , он назвал рассматриваемый логарифм l логарифмом по основанию a и заметил, что l ( a ) = 1 . Согласно этому соответствию существует число, названное Эйлером e, проверяющим эквивалентность , это число проверяет ln ( e ) = 1 . Экспоненциальная функция, допускающая разложение в целочисленный ряд , Эйлер получает разложение е как ряд обратных факториалов натуральных целых чисел.
вzзнак равноy⇔zзнак равнол(y){\ displaystyle a ^ {z} = y \ Leftrightarrow z = l (y)}еzзнак равноy⇔zзнак равнопер⁡(y){\ displaystyle \ mathrm {e} ^ {z} = y \ Leftrightarrow z = \ ln (y)}

По словам Эрве Ленинга, у него была бы «абсолютно блестящая интуиция, чтобы записать экспоненту с основанием a any как полином от экспоненты»  :

вИксзнак равноВ+BИкс+ПРОТИВИкс2+DИкс3+EИкс4+⋯{\ displaystyle a ^ {x} = A + Bx + Cx ^ {2} + Dx ^ {3} + Ex ^ {4} + \ cdots}

Он будет выражать все коэффициенты на основе B . Вот как. Сначала, полагая x = 0 , он получает A = 1 . Затем он вычисляет:

в2Иксзнак равно1+B(2Икс)+ПРОТИВ(2Икс)2+D(2Икс)3+E(2Икс)4+⋯{\ displaystyle a ^ {2x} = 1 + B (2x) + C (2x) ^ {2} + D (2x) ^ {3} + E (2x) ^ {4} + \ cdots}

в2Иксзнак равно1+2BИкс+4ПРОТИВИкс2+8DИкс3+16EИкс4+⋯{\ displaystyle a ^ {2x} = 1 + 2Bx + 4Cx ^ {2} + 8Dx ^ {3} + 16Ex ^ {4} + \ cdots}

но поскольку a 2 x = ( a x ) 2 , он также устанавливает

(вИкс)2знак равно(В+BИкс+ПРОТИВИкс2+DИкс3+EИкс4+⋯)2{\ displaystyle {(a ^ {x})} ^ {2} = (A + Bx + Cx ^ {2} + Dx ^ {3} + Ex ^ {4} + \ cdots) ^ {2}}

следовательно,

1+2BИкс+4ПРОТИВИкс2+8DИкс3+16EИкс4+⋯знак равно(1+BИкс+ПРОТИВИкс2+DИкс3+EИкс4+⋯)2{\ displaystyle 1 + 2Bx + 4Cx ^ {2} + 8Dx ^ {3} + 16Ex ^ {4} + \ cdots = (1 + Bx + Cx ^ {2} + Dx ^ {3} + Ex ^ {4} + \ cdots) ^ {2}}

Он развивает правую конечность, так что он может идентифицировать коэффициенты слева и справа: 2 B = 2 B , 4 C = B 2 + 2 C (следовательно, C = B 2 ⁄ ₂ ), 8 D = 2 D. + 2 BC (следовательно, D = B 3 ⁄ ₆ ) и  т. Д.

Поэтому он приходит к следующему уравнению:

вИксзнак равно1+BИкс+B22Икс2+B36Икс3+B424Икс4+⋯{\ displaystyle a ^ {x} = 1 + Bx + {\ dfrac {B ^ {2}} {2}} x ^ {2} + {\ dfrac {B ^ {3}} {6}} x ^ { 3} + {\ dfrac {B ^ {4}} {24}} x ^ {4} + \ cdots}

Поскольку основание e является единственным, допускающим равенство между экспонентой и ее производной, остается найти B такое, что этот многочлен и его производная равны. Решение тривиально: B = 1 . Наконец, мы замечаем, что 1, 2, 6, 24 — это последовательные значения факториала , из чего Эйлер приходит к выводу:

езнак равно1+11!+12!+⋯+1k!+⋯{\ displaystyle \ mathrm {e} = 1 + {\ dfrac {1} {1!}} + {\ dfrac {1} {2!}} + \ cdots + {\ dfrac {1} {k!}} + \ cdots}
приблизительное значение которого уже было вычислено Исааком Ньютоном в 1669 году.

Различные экспоненциальные кривые. Только основание e (синее) имеет тангенс угла наклона 1 в начале координат.

Различные характеристики экспоненциальной функции среди других экспоненциальных функций любой базы также помогают переопределить e как действительное, поскольку функция в x объединяет e x совпадает со своей производной в любой точке или только в точке (это эквивалентно) .

Определение логарифмами

Натуральный логарифм

Джон Напье .

В начале семнадцатого — го  века , шотландский математик Джон Напье построил первые логарифмические таблицы , которые позволяют упростить расчеты продуктов и дроби также квадратных корней , кубы и другие. Они заключаются в связывании с каждым номером списка другого числа (называемого логарифмом ), так что отношение пропорциональности между четырьмя элементами первого списка приводит к одинаковым различиям между соответствующими элементами второго списка: если a , b , c и d имеют соответствующие логарифмы , B , C и D , в то время как отношения _б = с_д эквивалентно отношению — B = C — D .

Точнее, Napier устанавливает начальный радиус в десять миллионов и строит список, в котором каждое число вычисляет следующее, вычитая одну десятимиллионную из своего значения. Эти последовательные операции поэтому умножения итеративны с 1 — 10 -7 и список представляет собой геометрическую последовательность из первого члена 10 7 . Логарифм каждого числа в списке является его рангом появления, затем формула логарифма, полученная таким образом Нэпьером, записывается:

NapLog⁡(Икс)знак равнобревно1-10-7⁡(Икс.10-7)знак равнопер⁡(Икс.10-7)пер⁡(1-10-7){\ displaystyle \ operatorname {NapLog} (x) = \ log _ {1-10 ^ {- 7}} (x.10 ^ {- 7}) = {\ frac {\ ln (x.10 ^ {- 7) })} {\ ln (1-10 ^ {- 7})}}}.

Napier интерпретирует эту конструкцию, используя кинематическую задачу, в которой один мобильный телефон движется с постоянной скоростью, а другой движется на конечную длину со скоростью, пропорциональной расстоянию, которое он должен преодолеть. Таким образом, говоря современным языком, проблема выражается в двух дифференциальных уравнениях , решения которых линейны для первого мобильного устройства и экспоненциально для второго. Уравняв начальные скорости двух мобильных устройств и зафиксировав длину пути для второго мобильного телефона на уровне 10 7 , положение L первого мобильного телефона получается из оставшегося расстояния x первого мобильного телефона по формуле:
Lзнак равно-107пер⁡(Икс.10-7).{\ displaystyle L = -10 ^ {7} \ ln (x.10 ^ {- 7}).}

Тем не менее, аффинное приближение натурального логарифма в 1 позволяет приблизиться к п (1 — 10 -7 ) от -10 -7 с точностью порядка 10 -14 , то есть сказать , 7 значащих цифр. Таблицы значений, полученные Napier, поэтому предлагают чтение тех же первых десятичных знаков, что и в натуральном логарифме, и, в частности, его логарифм равен 10 7 между синусами 21 ° 35 ‘и 21 ° 36, где мы находим первые дробную часть 1 / _м (т.е. 3678 …). Но Нэпье не выделяет это число.

Десятичный логарифм

В 1624 году корреспондент Нэпьера Генри Бриггс изменил параметры построения таблиц логарифмов. Сначала он устанавливает логарифм от 1 до 0, что равносильно выбору единицы радиуса. Затем его таблицы преобразуют продукты в суммы, которые записываются в современной формулировке: log ( ab ) = log ( a ) + log ( b ) . Затем он устанавливает логарифм 10 в 1, так что умножение числа на 10 приводит к добавлению одной единицы к его логарифму.

Таким образом, Бриггс получает таблицу значений десятичного логарифма , основанную на системе счисления с основанием 10, но понятие функции в то время еще не появилось. В частности, нет никаких следов оценки скорости увеличения 1, которая могла бы привести к приближению log (e) .

Натуральный логарифм

В 1647 году Грегуар де Сен-Винсент продемонстрировал связь, аналогичную логарифму между областями областей, ограниченными ветвью гиперболы, и ее асимптотой . В 1661 году Кристиан Гюйгенс установил связь между логарифмами и квадратурой гиперболы, в частности, уравнения x y = 1 . Поэтому натуральный логарифм выделен, но его основание ( e ) не идентифицировано.

В письме Лейбница к Гюйгенсу это число окончательно определено как основание натурального логарифма, около 1690 года, но Лейбниц отмечает это b .

Новый рейтинг

Леонард Эйлер .

Эйлер в статье, написанной в 1727 или 1728 году, первым отметил е «число, логарифм которого является единицей» . Он использует это обозначение с тем же определением в письме к Гольдбаху в 1731 году.

Выбор буквы e как дань уважения имени самого Эйлера поэтому маловероятен, были выдвинуты другие предположения: первая гласная или первая буква не используются в буквальном вычислении , инициал «экспоненты» и  т. Д. .

Число Эйлера в природе

Показатели с основанием e известны как естественные показатели, и вот почему. Если вы построите график

у = е ^ х

вы получите кривую, которая растет экспоненциально, как если бы вы построили кривую с основанием 10 или любым другим числом. Однако криваяу= eИксимеет два особых свойства. Для любого значенияИкс, значениеуравно значению наклона графика в этой точке, а также площади под кривой до этой точки. Это делает e особенно важным числом в математическом анализе и во всех областях науки, которые его используют.

Логарифмическая спираль, которая представлена ​​уравнением

г = п.в. ^ {bθ}

встречается в природе в ракушках, окаменелостях и цветах. Более того, e появляется во многих научных контекстах, включая исследования электрических цепей, законов нагрева и охлаждения, а также демпфирования пружин. Несмотря на то, что оно было открыто 350 лет назад, ученые продолжают находить новые примеры числа Эйлера в природе.

Закон радиоактивного распада

По поводу десяти грамм радия в шкафу я конечно пошутил, но, так или иначе, закон радиоактивного распада можно представить в виде следующего уравнения:

или

Если решите считать радиоактивные атомы не в штуках, а в привычных килограммах и граммах.

Где — изначальная масса радиоактивного вещества, — то что останется спустя время . На, а — это постоянная распада (статистическая вероятность распада атома за единицу времени)

Обратите внимание на минус в степени над числом. Минус будет говорить нам о том что количество радиоактивного вещества будет убывать

Хотя чаще всего в учебниках вы можете встретить другое уравнение:

Здесь — это так называемый период полураспада, время за которое распадается половина радиоактивного вещества.

Половина это когда . А если вспомнить что такое натуральный логарифм () и зачем он нам нужен, то можно из первого уравнения выразить период полураспада через радиоактивную постоянную:

В общем можете вооружиться ручкой, бумагой и на досуге из этого:

получить это:

Ну а если из всего сказанного вы не поняли ровным счетом ничего. И как говорил Виктор Степанович Черномырдин: «Всё это так прямолинейно и перпендикулярно, что мне неприятно». Не расстраивайтесь, по крайней мере, теперь Вы знаете как легко запомнить в каком году родился Лев Николаевич Толстой.

Единицы измерения, обозначаемые буквой Е

В науке и технике часто используются различные единицы измерения, которые обозначаются буквой Е. Эти единицы имеют свои специфические значения и применяются в разных областях знания.

Ниже приведен список некоторых единиц измерения, обозначаемых буквой Е:

• Электронвольт (эВ) — единица энергии в физике. Один электронвольт равен энергии, которую приобретает электрон, перемещаясь через электрическое поле с напряжением в один вольт.
• Эксабайт (ЭБ) — единица информации, равная 2 в степени 60 байт. Эта единица используется для обозначения больших объемов данных, таких как объемы информации на жестких дисках и в сетях.
• Экзаампер (ЭА) — единица электрического тока. Один экзаампер равен одному квинтиллиону ампер.

В таблице приведены еще некоторые единицы измерения, обозначаемые буквой Е:

Единица измерения	Значение
Эрг	единица энергии в системе СГС (Сантиграмм-сантиметр-секунда)
Эрланг (Е)	единица измерения загруженности системы в телекоммуникациях
Энзимная единица (ЕД)	единица измерения активности фермента

Это только некоторые примеры единиц измерения, обозначаемых буквой Е. В различных научных и технических областях могут использоваться и другие единицы, обозначаемые этой буквой, каждая со своими уникальными значениями и применениями.

Мнемоника[править | править код]

• Приблизительное значение зашифровано в: «Мы порхали и блистали, но застряли в перевале; не признали наши крали авторалли» (то есть 2,718281828459 )
• Запомнить как 2, 71, и повторяющиеся 82, 81, 82
• Мнемоническое правило: два и семь, далее два раза год рождения Льва Толстого (), затем углы равнобедренного (45, 90 и 45 градусов). Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой»
• Цифры 45, 90 и 45 можно запоминать как «год победы над фашистской Германией, затем дважды этот год и снова он»
• Правила e связывается с президентом США Эндрю Джексоном: 2 — столько раз избирался, 7 — он был седьмым президентом США,  — год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем — опять-таки равнобедренный прямоугольный треугольник.
• С точностью до трёх знаков после запятой через «число дьявола»: нужно разделить 666 на число, составленное из цифр 6 − 4, 6 − 2, 6 − 1 (три шестёрки, из которых в обратном порядке удаляются три первые степени двойки): 666245≈2,718{666 \over 245} \approx 2,718.
• Запоминание e как 66610⋅666−13\frac{666}{10 \cdot \sqrt{666} — 13}.
• Грубое (с точностью до 0,001), но красивое приближение полагает e равным π⋅cos Косинус π6\pi \cdot \cos {\pi \over 6}. Совсем грубое (с точностью 0,01) приближение даётся выражением 5⋅π−135 \cdot \pi — 13.
• «Правило Боинга»: e≈4⋅sin Синус ,747e \approx 4 \cdot \sin 0,747 даёт неплохую точность 0,0005.
• Формулы Г. Александрова: e≈3−563 e \, \approx \, 3 \, — \, \sqrt {\frac {5}{63}} — дает верные семь первых цифр, а e≈3−9394337\,e \, \approx \, 3 — \frac {93}{94} \sqrt { \frac {3}{37}} вычисляет константу с точностью 4,6⋅10−10 4,6 \, \cdot \, 10^{-10}.
• Стишки:

Два и семь, восемнадцать,

Двадцать восемь, восемнадцать,

Двадцать восемь, сорок пять,

Девяносто, сорок пять.

Символы вероятности и статистики

Символ	Название символа	Значение / определение	пример
P ( А )	функция вероятности	вероятность события A	P ( A ) = 0,5
P ( A ⋂ B )	вероятность пересечения событий	вероятность того, что событий A и B	P ( A ⋂ B ) = 0,5
P ( A ⋃ B )	вероятность объединения событий	вероятность того, что событий A или B	P ( A ⋃ B ) = 0,5
P ( A | B )	функция условной вероятности	вероятность события A данное событие B произошло	P ( A | B ) = 0,3
f ( x )	функция плотности вероятности (pdf)	P ( a ≤ x ≤ b ) = ∫ f ( x ) dx
F ( х )	кумулятивная функция распределения (cdf)	F ( х ) = Р ( Х ≤ х )
μ	Средняя численность населения	среднее значение совокупности	μ = 10
E ( X )	ожидаемое значение	ожидаемое значение случайной величины X	E ( X ) = 10
E ( X | Y )	условное ожидание	ожидаемое значение случайной величины X с учетом Y	E ( X | Y = 2 ) = 5
var ( X )	отклонение	дисперсия случайной величины X	var ( X ) = 4
σ 2	отклонение	дисперсия значений совокупности	σ 2 = 4
std ( X )	стандартное отклонение	стандартное отклонение случайной величины X	std ( X ) = 2
σ X	стандартное отклонение	значение стандартного отклонения случайной величины X	σ X = 2
	медиана	среднее значение случайной величины x
cov ( X , Y )	ковариация	ковариация случайных величин X и Y	cov ( X, Y ) = 4
корр ( X , Y )	корреляция	корреляция случайных величин X и Y	корр ( X, Y ) = 0,6
ρ X , Y	корреляция	корреляция случайных величин X и Y	ρ X , Y = 0,6
∑	суммирование	суммирование — сумма всех значений в диапазоне ряда
∑∑	двойное суммирование	двойное суммирование
Пн	Режим	значение, которое чаще всего встречается в популяции
MR	средний диапазон	MR = ( x макс + x мин ) / 2
Мкр	медиана выборки	половина населения ниже этого значения
Q 1	нижний / первый квартиль	25% населения ниже этого значения
2 квартал	медиана / второй квартиль	50% населения ниже этого значения = медиана выборки
3 квартал	верхний / третий квартиль	75% населения ниже этого значения
х	выборочное среднее	среднее / среднее арифметическое	х = (2 + 5 + 9) / 3 = 5,333
с 2	выборочная дисперсия	оценщик дисперсии выборки населения	s 2 = 4
с	стандартное отклонение выборки	Оценка стандартного отклонения выборки населения	s = 2
z x	стандартная оценка	z x = ( x — x ) / s x
X ~	распределение X	распределение случайной величины X	X ~ N (0,3)
N ( μ , σ 2 )	нормальное распределение	гауссово распределение	X ~ N (0,3)
U ( а , б )	равномерное распределение	равная вероятность в диапазоне a, b	Х ~ U (0,3)
ехр (λ)	экспоненциальное распределение	f ( x ) = λe — λx , x ≥0
гамма ( c , λ)	гамма-распределение	f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0
χ 2 ( к )	распределение хи-квадрат	f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2))
F ( k 1 , k 2 )	F распределение
Корзина ( n , p )	биномиальное распределение	f ( k ) = n C k p k (1 -p ) nk
Пуассон (λ)	распределение Пуассона	е ( К ) знак равно λ К е — λ / К !
Геом ( p )	геометрическое распределение	f ( k ) = p (1 -p ) k
HG ( N , K , n )	гипергеометрическое распределение
Берн ( p )	Распределение Бернулли

Что же такое число е и откуда оно взялось?

Кто-то спросит: «Что же это за число такое удивительное?» И здесь всего три слова: “второй замечательный предел”. На языке математики это выглядит следующим образом:

Расходимся…

Появление числа е связывают с Якобом Бернулли, который еще в 17 веке задался вопросом: какова же максимальная величина процентного дохода при постоянной капитализации вклада?

Якоб Бернулли (1654-1705)

Чтобы было понятно о чем идет речь, давайте представим, что у меня есть рубль. Я кладу его в банк под 100% годовых. То есть, через год у меня уже не рубль, а два.

Но что если рост происходит не мгновенно в конце года, а частями? Ну скажем, каждые полгода по 50%. Да, наш рубль так же превратится в два, но на 50 копеек, которые набежали за первые полгода, за вторую половину года набежит уже свой процент. И мы получим еще 25 копеек дополнительно. И в итоге мы имеем уже 2 рубля 25 копеек.

Если рост вклада будет происходить каждые четыре месяца, то есть 3 раза в год, дополнительный процент к нашим двум рублям, составит уже 37 копеек.

При ежемесячном росте только на процентах у нас набежит примерно 61 копейка.

И здесь возникает вопрос: а что если рост будет происходить непрерывно? Как в природе. К примеру, дети не вырастают на 15 сантиметров в свой день рождения. Нет. Они растут в течении всего года. Каждый день, каждый час, каждую секунду… Что если так же будет расти наш вклад, и вместе с ним будут увеличиваться начисления по проценту?

Существует ли какой то предел при непрерывном росте, который позволит понять, на какую максимальную прибыль мы можем рассчитывать?

Сам Бернулли определил, что это где-то между 2,5 и 3.

Леонард Эйлер (1707 – 1783)

Более точно этот предел вычислил Леонард Эйлер, а полученное число, к которому этот предел стремится, назвал числом е.

По одной из версий е — это первая буква в фамилии ученого (Euler). Но это не точно. Вполне возможно, что е это просто первая буква в слове«экспоненциальный» (exponential). Что тоже кажется тоже вполне разумным, так как экспонента, наверно, первая ассоциация при упоминании числа е. По крайней мере, у меня.

Приглядимся поближе

Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение?

Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

Однако и этим число Эйлера не будет ограничено.

Таким образом данное число представимо в виде бесконечной дроби, рекурсивной функции, ряда и предела.

Давайте уже разберем что же это за число.

Когда мы берем за основание число 1+1/n, близкое к единице, например 1,00001, то для небольших чисел получаются огромные логарифмы, например число 3 имеет логарифм 109861. Чтобы этот логарифм был величиной того же порядка, что и число 3, его следует уменьшить в 100000 раз. Тогда он имел бы величину 1,09861. Число 3 будет иметь логарифм 1,09861, если за основание взять не 1+1/n равное 1,00001, а (1+1/n)^n равное 1,00001^100000. Если мы найдем величину 1,00001^100000, то с точностью до восьмого знака найдем (1+1/n)^n при n равное 100000, будет равно 2,71826763

Обратите внимание это число очень близко к числу e

Таким образом чем больше взять число n, тем меньше число формулы (1+1/n)^n будет отличаться от числа e. Иначе говоря, число e есть предел, к которому стремится (1+1/n)^n , при неограниченном возрастании числа n.

Играет важную роль в дифференциальном и интегральном исчислении, а также многих других разделах математики.

2,718 281 828 459 045 235 360 287 471 352 662 497 757…

Где используется число е

Число е можно встретить в первую очередь там, где идет речь о процесах экспоненциального роста. То есть в случае использования функции f(x)=ex. Число е в степени X — это экспонента!

Самый наглядный пример, это рост числа популяции, например бактерий. Их количество будет экспоненциально возрастать, пока не достигнет предела, например, не кончится место для дальнейшего роста или питательная среда (будет нечего есть).

Также можно встретить число е в формулах для радиоактивного распада. Химические реакции, тоже развиваться по экспоненциальному закону где используется число е. Например, зависимость энергии активации и скорости химической реакции.

Зарядка и разрядка конденсатора тоже описывается экспоненциальным законом, с использованием числа Эйлера.

Еще число Эйлера используется в функции нормального распределения. Эта функция показывает распределение случайно величины, например, роста или веса котов, коэффициента интеллекта людей или то как далеко может укатится средняя пищика от того места где было высыпано ведро с песком.

То есть число е используется довольно часто. И встречается и в математике, и в физике и в биологии и, особенно, в экономике.