Задачи на делимость (сложная делимость)
Это задачи уже повышенной сложности. Предварительно советуем изучить тему . Обязательно к прочтению только тем, кто собирается занимать призовые места.
Для скольких чисел между и верно следующее утверждение: число делится на или не делится на ?
Такое страшное и непонятное условие становится простым, если воспользоваться кругами Эйлера
. Понятно, что в этой задаче рассматриваются числа, которые — нас интересуют те, что внутри соответствующего круга. Также есть числа, которые vdots 12 — нас интересуют числа, которые вне. А что же с числами, которые принадлежат обоим множествам? Во-первых, каким общим свойством они обладают, а во-вторых, интересуют ли они нас?
Сначала ответим на первый вопрос. Оказывается, если число одновременно делится на два других числа, то оно делится на Наименьшее Общее Кратное
этих двух чисел, то есть на минимальное число, которое делится без остатка на оба исследуемых. Для чисел и НОК есть ничто иное, как число , так как и , а меньше числа с такими свойствам нет. Итого, в пересечении наших множеств лежат числа, которые .
Далее необходимо заметить, что в условии употреблено слово «ИЛИ»
. Это значит, что для искомых чисел должно быть верно ХОТЯ БЫ ОДНО из предложенных утверждений (возможно и оба). То есть нам подходят числа которые внутри круга чисел, которые , а также все числа, которые вне круга .
Итак, диаграмма Эйлера-Венна
выглядит следующим образом:
Штриховкой обозначены те числа, которые и надо найти. Теперь, надеюсь, очевидно, что нам необходимо найти, сколько всего числе в рассматриваемой задаче, из этого количества вычесть количество чисел, которые и прибавить количество чисел, которые .
Итак, приступим:
Итак, подведём итог. Если Вы собираетесь поступать в 5 класс физико-математического лицея
, то общие знания по кругам Эйлера-Венна
Вам необходимы. Основная область применения — задачи, где присутствуют множества объектов, обладающих определёнными свойствами, и необходимо найти количество объектов обладающих (или не обладающих) совокупностью указанных свойств.
Отношения между множествами
Также следует различать понятия элементов и множества, объем которых отображают круги Эйлера. Понятие множества заимствовано из математической науки и имеет достаточно широкое значение. Примеры в логике и математике отображают его как некую совокупность объектов. Сами же объекты являются элементами данного множества. «Множество есть многое, мыслимое как единое» (Георг Кантор, основатель теории множеств).
Обозначение множеств осуществляется заглавными буквами: А, В, С, D… и т. д., элементов множеств – строчными: а, b, с, d…и др. Примерами множества могут быть студенты, находящиеся в одной аудитории, книги, стоящие на определенной полке (или, например, все книги в какой-либо определенной библиотеке), страницы в ежедневнике, ягоды на лесной поляне и т. д.
В свою очередь, если определенное множество не содержит ни одного элемента, то его называют пустым и обозначают знаком Ø. Например, множество точек пересечения параллельных прямых, множество решений уравнения х2 = -5.
Круги Эйлера и примеры задач на логику
На самом деле, круги Эйлера очень часто встречаются в нашей жизни. Уже в начальной школе ученики начинают работать со схематическими диаграммами, которые наглядно объясняют взаимосвязь между объектами и понятиями.
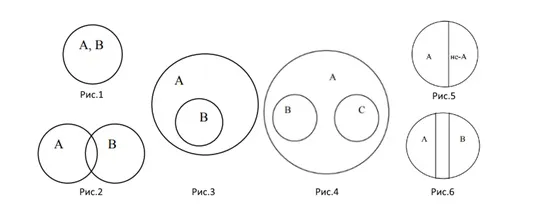
Эйлеровы круги — это геометрические структуры, используемые для упрощения распознавания рациональных отношений между объектами, понятиями и явлениями.
В зависимости от типа отношений между множествами, они делятся на группы.
- равнозначные (рис.1);
- пересекающиеся (рис.2);
- подчиненные (рис.3);
- соподчиненные (рис.4);
- противоречащие (рис.5);
- противоположные (рис.6).
Типичные примеры таких диаграмм:.
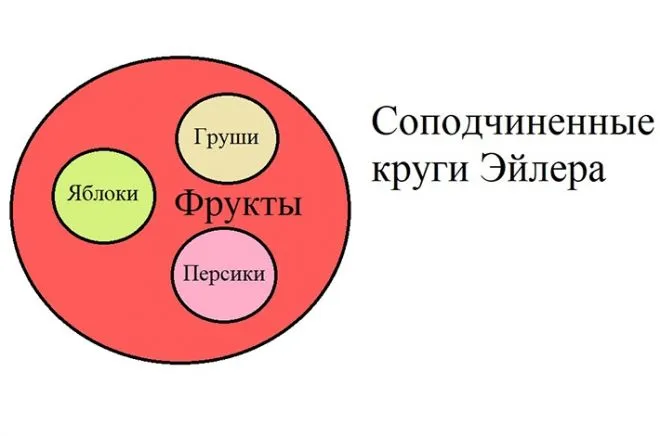
Самый большой зеленый набор представляет все вариации игры.
Одним из вариантов игры является производитель. Он отмечен синим овалом. Мейкер — это независимый набор и в то же время часть всей «игры».
Игры с часами также являются частью набора «Игры», но не являются частью общего набора «Создатель». Поэтому они отмечены фиолетовым овалом. Набор «курдские автомобили», с другой стороны, является независимым набором, но подмножеством набора «курдские игры».
Используя этот метод, ученые решали самые сложные математические задачи. Используя простые формы, они смогли свести любое решение к символической логике, то есть к максимальной простоте рассуждений, даже для самых сложных задач.
Затем метод был доработан Джоном Бенном в Великобритании, который ввел понятие множества наборов пересечений.
Методология очень проста в использовании — эйлеровский цикл уже преподается в детских садах для 4-5-летних детей. Однако он также достаточно прост для использования в высшей академической среде.
Противоречие (контрадикторность)
В данном случае оба понятия представляют собой виды одного и того же рода. Как и в предыдущем примере, одно из понятий указывает на определенные качества (признаки), в то время как другое их отрицает. Однако, в отличие от отношения противоположности, второе, противоположное понятие, не заменяет отрицаемые свойства другими, альтернативными. Например:
А – сложная задача;
В – несложная задача (не-А).
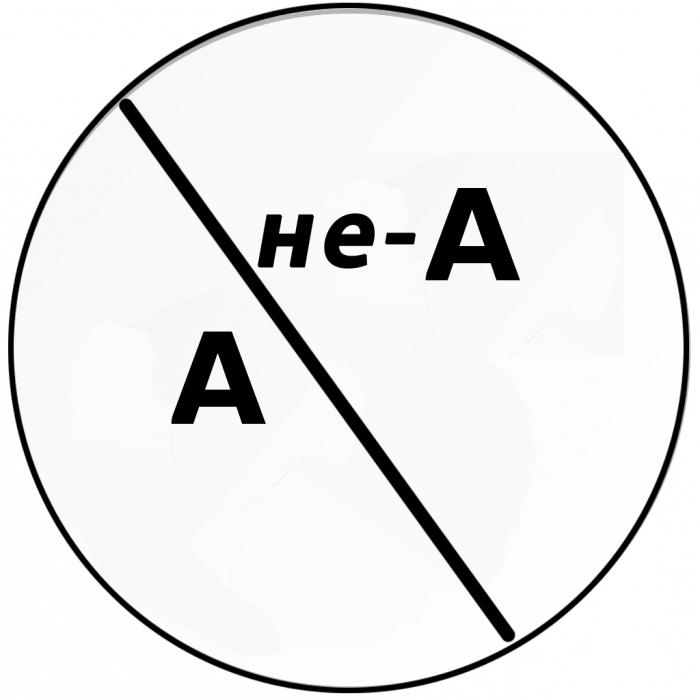
Выражая объем понятий подобного рода, круг Эйлера разделяется на две части – третьего, промежуточного звена в данном случае не существует. Таким образом, понятия также являются антонимами. При этом одно из них (А) становится положительным (утверждающим какой-либо признак), а второе (В или не-А) – отрицательным (отрицающим соответствующий признак): «белая бумага» – «не белая бумага», «отечественная история» – «зарубежная история» и т. д.
Таким образом, соотношение объемов понятий по отношению друг к другу является ключевой характеристикой, определяющей круги Эйлера.
Отношения между понятиями
Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.
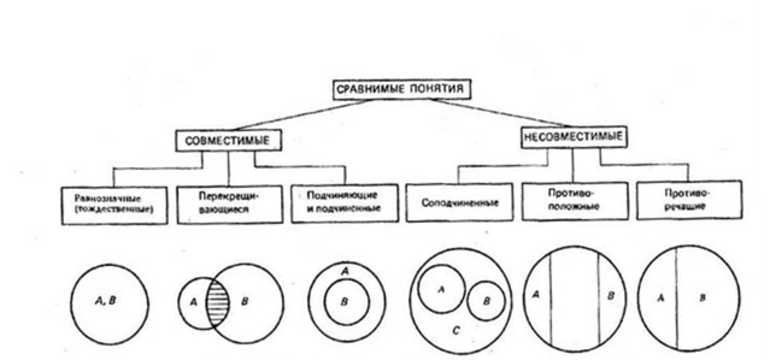
Рисунок 1
Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:
- равнозначные (тождественные);
- перекрещивающиеся;
- подчиняющие и подчинённые.
У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).
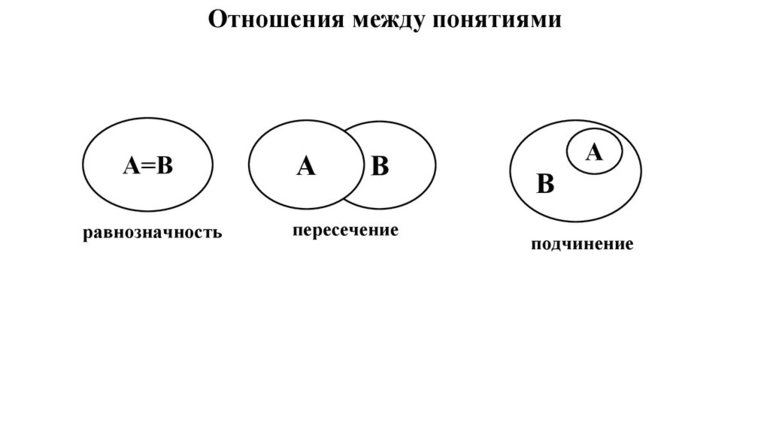
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.
Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».
Несовместимыми называют понятия, не имеющие общих элементов:
- соподчинённые;
- противоположные;
- противоречащие.
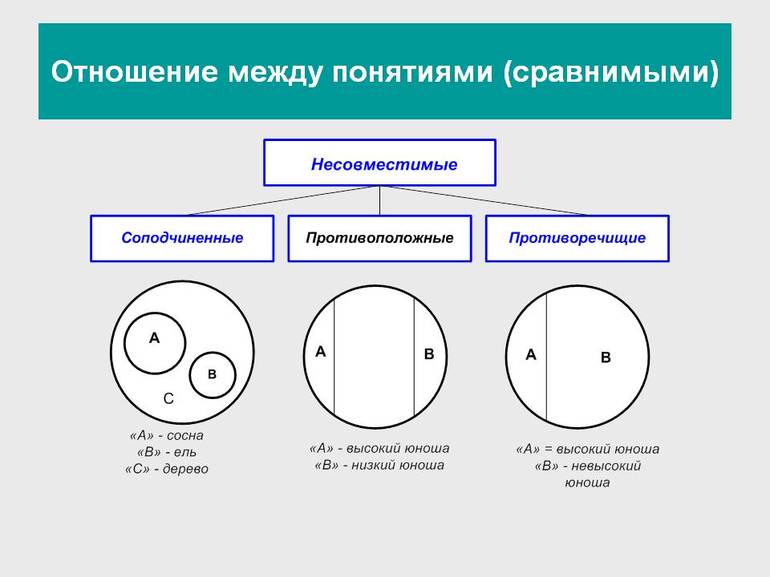
Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.
Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).
Справочная информация
ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной
Круговые схемы Эйлера и диаграммы Венна для выражения отношений между понятиями
Разделительная связка
в языке обычно выражается с помощью
союзов «или», «либо».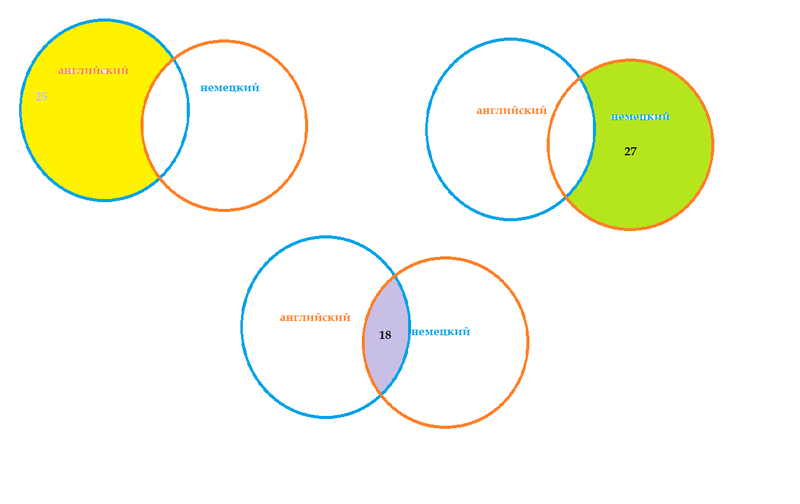
Полная и
неполная дизъюнкция. Среди дизъюнктивных суждений следует
различать полную и неполную дизъюнкцию.
Полным или закрытым называют дизъюнктивное
суждение, в котором перечислены все признаки
или все виды определенного рода.
Символически это суждение
можно записать следующим образом:
<р v q v r>.
Например: «Леса бывают
лиственные, хвойные или смешанные».
Полнота этого разделения (в символической записи
обозначается знаком <…>) определяется
тем, что не существует, помимо указанных,
других видов лесов.
Неполным или
открытым называют дизъюнктивное суждение,
в котором перечислены не все
признаки или не все виды определенного рода.![]()
р v q v r v…
В естественном языке
неполнота дизъюнкции выражается словами:
«и т.д.», «и др.», «и тому подобное», «иные»
и другими.
3. Условные (импликативные)
суждения.5
Условным, или импликативным,
называют суждение, состоящее из двух
простых, связанных логической связкой
«если.., то…». Например: «Если предохранитель
плавится, то электролампа гаснет». Первое
суждение — «Предохранитель плавится»
называют антецедентом (предшествующим), второе — «Электролампа
гаснет» — консеквентом (последующим).
Если антецедент обозначить р,консеквент
— q, а связку «если…, то…» знаком «»,
то имплика-тивное суждение символически
можно выразить как рq.
В естественном языке для выражения условных суждений используется
не только союз«если…, то…», но и другие
союзы: «там…, где», «тогда…, когда…», «постольку…, поскольку…» и
т.п. В форме условных суждений в языке
могут быть представлены такие виды объективных
связей, как причинные, функциональные,
пространственные, временные, правовые,
а также семантические, логические и другие
зависимости.![]()
В форме условных суждений
нередко выражают логические зависимости
между высказываниями. Например: «Если
верно, что некоторые птицы улетают зимой в теплые края, то неверно, что ни
одна птица не улетает в теплые края».
В условном суждении антецедент
выполняет функцию фактического или
логического основания, обусловливающего
принятие в консеквенте соответствующего
следствия. Зависимость между антецедентом-основанием и консеквентом-следствием
характеризуется свойствомдостаточности. Это
означает, что истинность основания обусловливает
истинность следствия, т.е. при истинности
основания следствие всегда будет истинным.
При этом основание не характеризуется
свойством необходимости для следствия,
ибо при его ложности следствие может
быть как истинным, так и ложным .![]()
4. Эквивалентные
суждения (двойная импликация).
Эквивалентным, называют суждение, включающее
в качестве составных два суждения,
связанных двойной (прямой и обратной)
условной зависимостью, выражаемой логической
связкой «если и только если…, то…». Например:
«Если и только если человек награжден
орденами и медалями (р), то он имеет право на
ношение соответствующих орденских планок
(q)».
Логическая характеристика
этого суждения состоит в том,
что истинность утверждения о
награждении (р) рассматривается как необходимое и
достаточное условие истинности утверждения
о наличии права на ношение орденских
планок (q). Точно так же истинность
утверждения о наличии права на ношение
орденских планок (q) является необходимым
и достаточным условием истинности утверждения
о том, что данное лицо награждено соответствующими
орденом или медалью (р).
В естественном языке
для выражения эквивалентных суждений используют союзы: «лишь при условии что…, то.![]()
Рис. 1.1 «таблицы истинности»
3.Тест:
Суждение «Бога нет» является:
а) релятивным;
б) атрибутивным;
в) экзистенциональным;
г) конъюнктивным
Ответ: в)
Список используемой
литературы
- Кириллов В.И., Старченко А.А. Логика: учебник. – М.: Юристъ, 2008.
–
с.230
- Гетманова А.Д. Учебник по логике. 2-ое изд. – М.: «ВЛАДОС», 1995.
– с. 304
- Логика;электронно-Библиотечная Система,учебное пособие; Батурин В.К./Москва 2012
1 Логика;электронно-Библиотечная Система,учебное
пособие; Батурин В.К./Москва 2012
2 Кириллов В.![]()
3 Логика;электронно-Библиотечная Система,учебное
пособие; Батурин В.К./Москва 2012
Гетманова А.Д. Учебник по логике. 2-ое
изд. – М.: «ВЛАДОС», 1995.– с. 304
4 Логика;электронно-Библиотечная Система,учебное
пособие; Батурин В.К./Москва 2012
5 Логика;электронно-Библиотечная Система,учебное
пособие; Батурин В.К./Москва 2012
Где применяются круги Эйлера
Круги Эйлера широко используются во многих упражнениях на мышление и логику. Ученые сами применяют этот метод для решения сложных математических задач. Это объясняется тем, что простая форма схемы упрощает рассуждения и позволяет визуализировать возможные решения.
Сегодня круги Эйлера широко используются в его работе: круг Эйлера — это простая форма, которую можно использовать для визуализации решения сложной математической задачи.
Основным преимуществом этого метода является его гибкость. Развитие детского мышления и сложных математических (и не только!) способностей. проблемы.
Для чего нужны круги Эйлера
Круги Эйлера имеют прикладное значение, ведь с их помощью можно решать множество практических задач на пересечение или объединение множеств в логике, математике, менеджменте, информатике, статистике и т.д. Полезны они и в жизни, т.к., работая с ними, можно получать ответы на многие важные вопросы, находить массу логических взаимосвязей.
Есть несколько групп кругов Эйлера:
- равнозначные круги (рисунок 1 на схеме);
- пересекающиеся круги (рисунок 2 на схеме);
- подчиненные круги (рисунок 3 на схеме);
- соподчиненные круги (рисунок 4 на схеме);
- противоречащие круги (рисунок 5 на схеме);
- противоположные круги (рисунок 6 на схеме).
Посмотрите схему:
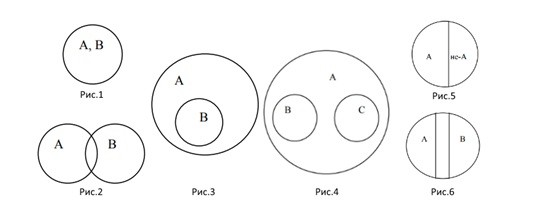
Но в упражнениях на развитие мышления чаще всего встречаются два вида кругов:
Круги, описывающие объединения понятий и демонстрирующие вложенность одного в другое. Посмотрите пример:
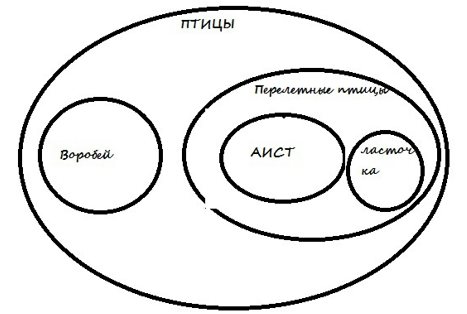
Круги, описывающие пересечения разных множеств, имеющих некоторые общие признаки. Посмотрите пример:
Результат использования кругов Эйлера проследить на этом примере очень просто: обдумывая, какую профессию выбрать, вы можете либо долго рассуждать, пытаясь понять, что больше подойдет, а можете нарисовать аналогичную диаграмму, ответить на вопросы и сделать логический вывод.
Применять метод очень просто. Также его можно назвать универсальным – подходящим для людей всех возрастов: от детей дошкольного возраста (в детских садах детям преподают круги, начиная с 4-5-летнего возраста) до студентов (задачи с кругами есть, к примеру, в тестах ЕГЭ по информатике) и ученых (круги широко применяются в академической среде).
Дополнение множества
Дополнением к множеству A является множество \(\overline A\), которое состоит из элементов, не входящих в А.
\(\overline A\;=\;\left\{x\;\vert\;x\;\not\in\;A\right\}\)
При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:
\(\overline A\;=\;U\;\backslash\;A\)
Таким образом выглядит дополнение \(\overline A\) графически:
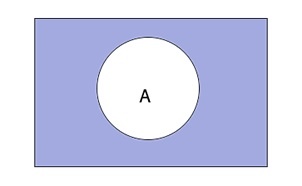
Решение задач, примеры
Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.
Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?
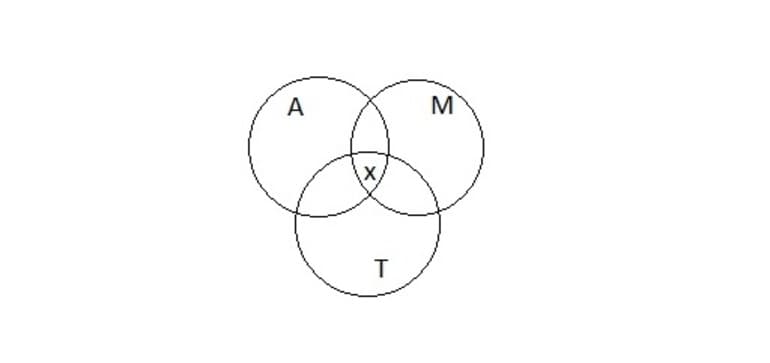
Рисунок 2
Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.
Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…
Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…
Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).
54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.
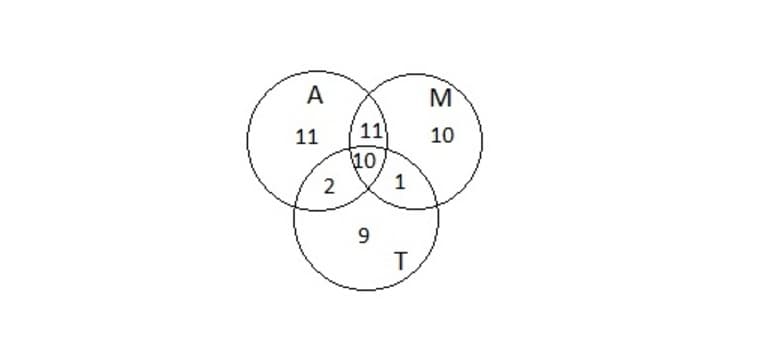
Рисунок 3
Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?
Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.
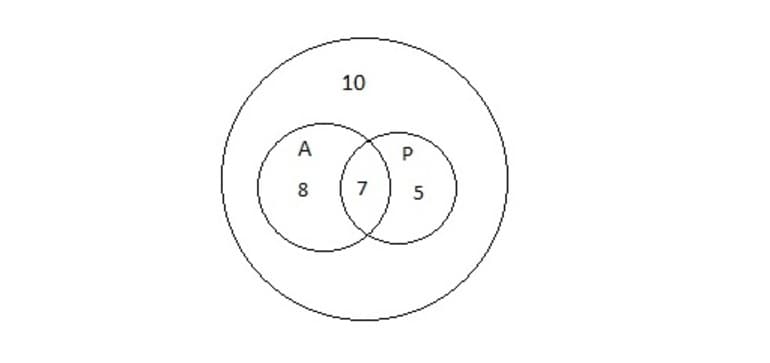
Рисунок 4
Круги Эйлера часто применяются для решения самых разных задач. Они служат для развития способности к логическому мышлению у дошкольников. Большой раздел задач для школьников может решаться с помощью диаграмм. Многие учёные в своих исследованиях тоже обращаются к этому методу, который повышает наглядность решаемых проблем и помогает в их обдумывании. Использование простых фигур позволяет свести решение любой сложной задачи к символической логике и упростить ход рассуждений. Диаграммы могут применяться и в обычной жизни, например при поиске работы. Пересечение кругов «лучше всего получается», «больше всего нравится делать» и «чем можно заработать», возможно, даст нужный результат.
Предыдущая
ИнформатикаКак сделать оглавление в ворде — алгоритм создания и примеры
Следующая
ИнформатикаФормула Шеннона — выводы, условия применения и примеры решения
Прием «Диаграмма Эйлера-Венна»
Организация: МБОУ СОШ №1
Населенный пункт: г. Мичуринск, Тамбовская область
Как организовать образовательный процесс так, чтобы научить детей учиться и подготовить человека думающего, выпускника, умеющего проявлять инициативу, независимость и ответственность в современном обществе? Этот вопрос волнует каждого учителя. И как любому учителю, мне хочется, чтобы мои уроки вызывали у детей интерес, заставляли самостоятельно мыслить, прививали им полезные для жизни и дальнейшей учебы умения и навыки. Для того чтобы дать детям возможность активно работать с получаемым знанием, на уроках я применяю прием «Кольца Венна», или «Диаграмма Эйлера -Венна » применяется в рамках технологии развития критического мышления ). Диаграмма Венна – это графический способ, с помощью которого можно выявить общее в сравниваемых областях, подчеркнуть различия и обобщить знания по выбранной теме.
Алгоритм работы с приемом «Диаграмма Эйлера -Венна »
1. На уроке выявляются два или более понятий, терминов, явлений, которые нужно сравнить.
2. Ученики рисуют кольца и заполняют графы.
3. На этапе осмысления (закрепления материала) происходит обсуждение составленных диаграмм (в парах, в группах).
Этот прием можно использовать на различных уроках. На уроке литературного чтения по теме: В Драгунский «Друг детства», учащиеся дали характеристику Дениске до встречи с другом и после, использовав два круга. 1 круг – до встречи (растерянный,весёлый, легкомысленный), 2 круг – после встречи с другом (верный, сердечный, внимательный, преданный), сходство – один круг накладывается на другой (мальчик, Дениска, добрый). Учащиеся делают вывод: любить и заботиться нужно не только о живых существах, но и об игрушках. Любимая игрушка – это как самый верный близкий друг. Он не обидится, не убежит, не даст сдачи, не предаст.И здесь Дениска повёл себя как настоящий друг.На уроке русского языка по теме: «Орфограммы в корне слова» (урок закрепления) учащиеся работали в группах. Первая группа – орфограммы гласных в корне слова — различие (безударные, ставлю под ударение), 2 группа — орфограммы согласных в корне слова – различие (парные звонкие и глухие, непроизносимые,на конце слова, в середине перед глухими(иногда перед звонкими) согласными, в звукосочетаниях , , , , , , проверяю- ставлю перед гласными и согласными л,м,н,р,в,й), 3 группа – сходство (орфограммы в корне слова, непроверяемые -запоминаю и уточняю в словаре).На уроке математики по теме: «Решаем задачи по действиям», работая в паре над составными задачами, учащиеся помогали друг другу выявлять различие и сходство в условии задач. Н-р: Мишутка выдумал 20 невероятных историй, а Стасик – в 5 раз меньше.Сколько всего историй выдумали ребята? 1 круг – Мишутка 20 историй, 2 круг – Стасик, в 5 раз меньше, сходство – невероятные истории, вопрос задачи. Это помогает правильно записать условие задачи, а затем и решить её. На уроке окружающего мира по теме: «Как изучали земной шар. Путешествия» в конце урока каждый учащийся закрепил свои знания по этой теме. 4 круга- 4 путешественника -4 различия (Христофор Колумб- Италия, открыл Америку, Афанасий Никитин – Россия, побывал в Индии, Фернандо Магеллан – Португалия, совершил кругосветное путешествие вокруг Земли, Руаль Амундсен –Норвегия,первым достиг Южный полюс), сходство-путешественники, первооткрыватели.
Уже сейчас я могу смело утверждать, что учащимся интересно работать с «Диаграммой Эйлера -Венна». Они быстро и легко находят различия и обобщают знания по выбранной теме. Каждый из них является исследователем, а это нравится как сильным, так и слабым ученикам.Это помогает вырабатывать умение искать, выбирать, систематизировать, анализировать и предлагать на суд товарищей выбранное и обдуманное решение, отстаивать свое мнение и с помощью товарищей, находить новые и интересные варианты ответов. Использование этого приема внесло в работу элемент творчества, повысило интерес к изучаемым темам, что подтвердило правильность моего выбора. Ведь данный прием направлен на развитие ученика, основными показателями которого являются оценочность, открытость новым идеям, собственное мнение и рефлексия собственных суждений.
Приложения:
-
file0.docx.. 20,7 КБ
Опубликовано: 15.04.2019
Резюме
Круги Эйлера – это очень полезная методика решения задач и установления логических связей, а заодно и занимательный и интересный способ провести время и потренировать мозг. Так что, если вам хочется совместить приятное с полезным и поработать головой, предлагаем пройти наш курс « », включающий в себя самые разные задания, в том числе и круги Эйлера, эффективность которых научно обоснована и подтверждена многолетней практикой.
Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).
Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.
Принцип кругов Эйлера
Помни про эмблему из «Зачарованных», она тебе понадобится для визуализации.

Круги Эйлера в реальной жизни
На самом деле, все гениальное просто и самая лучшая и простая техника с техникой Эйлера называется «три круга». Для использования этой несложной техники тебе понадобится три карандаша разного цвета и листок бумаги. Ловкость ума и никакого мошенничества, честно слово! Сейчас ты научишься мыслить ещё более рационально, чем до этого момента!
Помни, что один круг–один инструмент. Например: «что я люблю делать?», «что у меня получается лучше всего?», «как из этого извлечь выгоду или заработок?».
Рисуй круги.
Тут нам и понадобится эмблема из нашумевшего сериала. Нарисуй три круга (у каждого круга свой цвет), так, чтобы круги пересекались образовывая внутри трилистник.
Дай кругам названия.
Название круга – это инструмент, присвой каждому кругу свой. Раскрой полностью смысл каждого инструмента. Что-то нравится? Напиши почему нравится. Напиши о том, сколько ты хочешь зарабатывать, укажи причину – поставь себе цель. Напиши, почему у тебя получается делать что-то лучше, чем остальные, похвали себя.
Очень важно рисовать круги до тех пор, пока не образуется этот трилистник. Да, круги могут не пересекаться, тогда нужно думать, как сделать так, чтобы пересеклись, может быть, придётся заменять инструменты. Круги могут быть разного размера, фигура внутри не обязательно должна иметь равные части, самое главное, чтобы эти части были
Круги могут быть разного размера, фигура внутри не обязательно должна иметь равные части, самое главное, чтобы эти части были.
Теперь, когда ты нарисовала круги, распределила задачи, в самом центре появилась фигура похожая на треугольник–эта фигура является главным отношением между твоими «подмножествами», она даёт конечный результат. Получившиеся листки – это путь к конечному результату.
Пример решения задачи с помощью кругов Эйлера
| 58 человек ежедневно добираются на работу общественным транспортом: на автобусе, на трамвае или на метро. Каждый пользуется хотя бы одним из видов транспорта. 42 человека из них используют метро, 32 – трамвай, 44 – автобус. 21 человек из них используют метро и трамвай, 31 – метро и автобус, 22 – трамвай и автобус. Сколько среди них человек, которые используют все три вида транспорта, чтобы добраться на работу? |
Тут нужно понимать, что если сказано, что «42 человека используют метро», то это вовсе не означает, что кроме метро они не используют никаких других видов транспорта. Кто-нибудь из них может быть и использует. Может быть ещё какой-то один вид транспорта, трамвай или автобус. А может и сразу оба! Вопрос задачи как раз и состоит в том, чтобы посчитать людей, которые используют все три вида транспорта.
С первого взгляда даже непонятно, с чего начинать решение. Но если немного поразмыслить, становится ясно, что действовать нужно по следующему алгоритму. Будем стараться расписать всех людей (58 человек) через известные из условия данные. Нам известно, что автобус используют 44 человека. Прибавим к этому количество людей, которые используют метро. Их всего 42 человек. С помощью кругов Эйлера эту операцию можно изобразить наглядно в следующем виде:
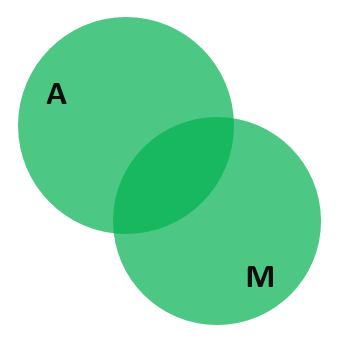
То есть пока что мы имеем дело с выражением 58 = 44 + 42… Знак «…» означает, что выражение ещё не закончено. Проблема в том, что мы посчитали людей на пересечении этих кругов дважды. Соответствующая область на диаграмме выделена тёмно-зелёным цветом. Поэтому один раз их нужно вычесть. Это люди, которые пользуются автобусом и метро. Их, как известно, 31. То есть наше «неоконченное» выражение принимает вид: 58 = 44 + 42 — 31… И на диаграмме при этом пропадает тёмно-зелёный цвет:
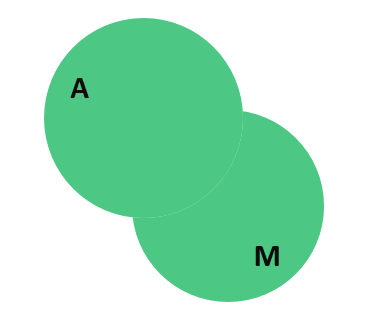
Пока всё хорошо. Прибавляем теперь людей, которые ездят на трамвае. Таких людей 32. Выражение принимает вид: 58 = 44 + 42 — 31 + 32… Диаграмма с кругами Эйлера, в свою очередь, становится следующей:
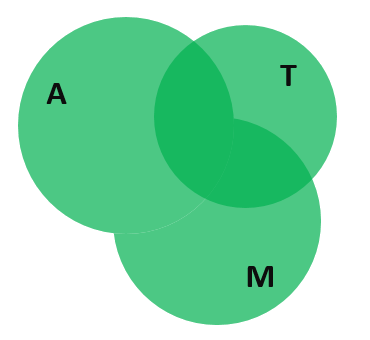
Проблема в том, что опять мы хватанули лишку. Люди, которых мы вновь посчитали дважды, отмечены на диаграмме тёмно-зелёным цветом. Эта область находится на пересечении множества, которое мы получили на предыдущем этапе, и множества людей, пользующихся трамваем.
Нужно вычесть людей, которых мы посчитали дважды. Но как это сделать? Единственное, что мы можем сделать, — это разом вычесть людей, которые передвигаются на трамвае и автобусе (их 22 человека), а также на трамвае и метро (таких людей 21). После этого наше неоконченное выражение для общего количества людей примет вид: 58 = 44 + 42 — 31 + 32 — 22 — 21…, а диаграмма с кругами Эйлера окажется с дыркой в центре, потому что центральную часть мы вычли дважды:
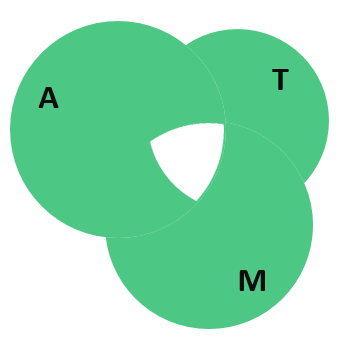
К счастью в незакрашенной области как раз и находятся те люди, число которых нам нужно посчитать. Действительно, эти бедняги используют ежедневно все три вида транспорта для того, чтобы добраться до работы, ведь они находятся на пересечении всех трёх множеств. Обозначим количество этих бедолаг за . Тогда диаграмма примет следующий вид:
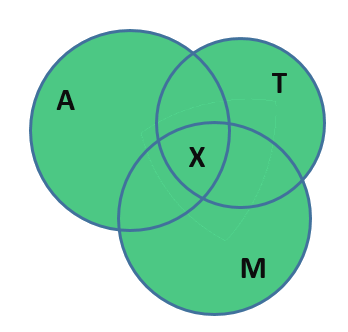
А уравнение станет следующим:
![]()
Расчёты дают . Это и есть ответ к задаче. Столько людей используют все три вида транспорта каждый день, чтобы добраться на работу.
Вот такое вот простое решение. Фактически, в одно уравнение. Просто удивительно, не правда ли?! А теперь представьте, как пришлось бы решать эту задачу без использования кругов Эйлера. Это было бы настоящее мучение. Так что в очередной раз убеждаемся, что любые методы визуализации чрезвычайно полезны при решении задач по математике. Используйте их, это поможет вам в решении сложных задач как на олимпиадах, так и на вступительных экзаменах по математике в лицеи и вузы.
Чтобы проверить, хорошо ли вы поняли решение данной задачи, ответьте на следующие вопросы:
- Сколько человек используют только один вид транспорта для того, чтобы добраться до работы?
- Сколько человек используют для этого ровно два вида транспорта?
Виды кругов Эйлера
Эйлер выделил шесть типов отношений между понятиями, выраженных в соответствующей форме.
- Равнозначные. Два одинаковых круга. Например, А.С.Пушкин = автор повести «Капитанская дочка».
- Пересекающиеся. Часть одного круга частично совпадает с частью другого (человек может быть одновременно и футболистом, и поэтом).
- Подчиненные. Один маленький круг внутри большого (корова относится к классу млекопитающих).
- Соподчиненные. Несколько одинаковых по размеру маленьких кругов внутри большого (яблоко, груша, персик – фрукты).
- Противоречащие. Разделенный пополам круг, каждая часть которого не имеет ничего общего с другой. Например, две конкурирующие между собой компании, производящие автомобили.
- Противоположные. Две части круга, между которыми есть свободное пространство. В отличие от предыдущей группы, между ними нет конфликта (холодное и горячее).



























