Фокус на 7
Вам понадобятся несколько игральных кубиков (костей). Скажите ребёнку, что, сколько бы костей он ни выбросил, вы сразу же скажете сумму точек на их верхних и нижних гранях — даже несмотря на то, что низ кубиков не видно.
Секрет прост: кубики устроены таким образом, что сумма точек на верхней и нижней поверхностях всегда равна 7. Таким образом, чтобы узнать правильный ответ, достаточно умножить количество брошенных кубиков на 7.
Предложите ребёнку показать фокус брату или сестре, бабушке с дедушкой, друзьям. Пусть школьник меняет число кубиков. Это поможет ему закрепить в памяти умножение на 7.
Совет в запоминании №1
Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.
Умножение – это сумма одинаковых слагаемых.
8 x 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8
Понимая смысл множителя, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.
Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.
Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее: 4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32
Умножать можно с помощью рук Умножение на 9
Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.
Вычисление произведения любых однозначных чисел больше, чем 5
Способ 1
Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).
Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.
Способ 2
Например, нужно выяснить сколько будет при счете 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.
В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42
Проверьте и убедитесь, что эти способы действительно работают.
Как еще можно выучить таблицу умножения легко и интересно
Современное поколение детей рождается с гаджетами в руках, обожает компьютерные игры и нескучные видео-ролики. Так почему бы не совместить приятное с полезным?
⠀
Специально для современных непосед мы сняли серию ярких обучающих роликов, которые помогут вашему ребенку понять принцип умножения при помощи простых и понятных приемов.
⠀
Например, как быстро умножить 6 на 7, а 7 на 8? Можно подсмотреть в таблицу Пифагора, можно вспомнить таблицу на плакате над учебным столом и даже достать калькулятор! А можно просто взглянуть на свои ладони и назвать правильный ответ.
Или, как можно научиться умножать на 9 быстрее, чем на 2? Делимся с вами самым простым и быстрым способом, который освоит ребенок, если умеет считать хотя бы до 10.
⠀
Закономерности в таблице умножения

Чтобы знать, как помочь ребенку быстро выучить таблицу умножения, разбирают закономерности математического действия. Вот некоторые из основных правил:
- Умножение на 1 на результат не влияет, число остается таким же.
- Примеры на 5 оканчиваются на 5 или 0. Если число четное (2, 4, 6), находим половину числа и приписываем 0. Если нечетное (3, 5, 7), половина является искомой и заканчивается на 5.
- При умножении на 10 итоговое число оканчивается на 0, начинается с того, на которое умножаем.
- Все примеры на 5 наполовину меньше, чем на 10 (10х5=50, 5х5 = 25).
- Умножение на 4 – это двойное увеличение чисел. Например, 2х4 – это 2+2 = 4, 4+4 = 8.
Помогите ребенку понять смысл умножения
Первое, что нужно сделать, — объяснить удобство умножения. Вы можете начать изучение таблицы умножения задолго до ее появления в школьной программе. Например, заранее расскажите, что существует такое волшебное математическое действие, которое позволяет не складывать поочередно одни и те же числа, а в одно действие получить результат. Поэтому родителям полезно знать, в каком классе учат таблицу умножения.
Наглядное чудо
Предположим, в семье есть традиция подсчитывать расходы за месяц. Попросите ребенка принять участие в домашней бухгалтерии. Он ведь у вас уже такой взрослый и даже сам ходит за хлебом!
Задание: посчитать, сколько денег потребуется, чтобы в течение месяца покупать хлеб по 20 рублей.
Возьмите простой перекидной календарь и пишите каждый день в нужной ячейке:
Пускай юный математик посчитает нарастающим итогом каждый день или сразу весь месяц. А потом просто покажите ему как волшебство единственное действие:
Этот прием — своеобразная презентация важного навыка. В результате родители получают неплохой мотивационный инструмент для ребенка: «Давай учить таблицу умножения, чтобы можно было легко и быстро считать»
Школа математических фокусов
Фокусы с числами не должны заканчиваться на подсчете семейного бюджета. Теперь предложите своему второкласснику самостоятельно найти взаимосвязь между сложением и умножением. Разберите с учеником задание-продолжение.
— Два дня подряд мы с тобой покупали чупа-чупсы по 9 рублей. Сколько денег мы на них потратили?
— 9+9 = 18 рублей, — ответит школьник.
— А если я буду покупать тебе такие конфеты всю неделю, сколько денег я потрачу?
— ?.. В неделе 7 дней, значит: 9+9+9+9+9+9+9=…, — задумается и станет долго считать. Позвольте ему дописать пример и получить 63.
— А давай попробуем посчитать по таблице умножения? Смотри (покажите таблицу на обороте тетради) — сколько дней подряд я покупаю конфеты?
— 7! — выберите столбец на 7.
— А сколько стоит каждая конфета?
— 9 рублей! — найдите строку на 9.
— Смотри, сколько получается?
— Тоже 63! Ого!
— Калькулятор тоже знает таблицу умножения. Смотри: 7 умножаем на 9, равно 63. Видишь, как быстро! Здорово?
— Да!
Ведите диалог занимательно, старайтесь увлекать ребенка, создавать интригу, указывать на «чудесные» свойства чисел, показывая на личном примере, как можно быстро умножать.
Другие удивительные и простые закономерности
Мальчики и девочки быстро понимают, что умножение — это облегченное сложение. Сразу же можно поведать и о других интересных закономерностях произведений:
Умножение на единицу: число, умноженное на единицу, остается неизменным. Тут удобно считать звезды или сто-тыщ-миллионы. И даже самое большое число не изменится при умножении на единицу.
«Я каждый день даю тебе в школу по 1 яблоку. Сколько яблок за неделю? А за 30 дней? А за 365?»
Умножение на ноль: даже самого большого в мире числа не будет, если его умножить на ноль. Можно что-то перекладывать из коробки в коробку и использовать синонимичное нулю слово «Ни разу».
«Ты каждый день уходишь и не берешь с собой яблоки. Сколько моих яблок ты не съешь в школе за неделю? А за 30 дней? А за 365?»
Умножение на 10
Здесь важно объяснить, куда дописывать нолик. В школе дети разбирают, что такое разряды и почему ноль дописывают именно справа
Дома достаточно повторить правило.
«Первый множитель «такой-то», второй — 10.
Чтобы получить значение произведения, нужно дописать нолик к первому множителю справа».
Умножение на 100, 1000 и более лучше пока отложить, если только ребенок сам не задаст вопрос.
Создаём таблицу Пифагора
Ура! Мы добрались до того, с чего все часто начинают. Но не все так быстро. Прежде чем начать, нужно уточнить, сформировано ли представление о чётных и нечётных числах
Это очень важно! Ряд чётных чисел — это таблица на 2, если прыгать через один шаг, то на 4, через 2 шага — на 6, через три шага — на 8… (потом с помощью этого ряда можно объяснять матрёшку возведения в степень)
Если мы вводим понятие, то очень удобно опереться на слово «чета», и вводить его нужно сразу после изучения темы «Число и цифра два. Два, две. Второй. Пара. Чета». Подойдут игры во всё, что можно объединить парами от балов до Ноева ковчега.
Если мы формируем представление, то подойдут все предметно-практические упражнения на соотношение множеств во время сравнения, путем наложения или приложения элемента из одного множества на элемент из другого множества, составляя пары. Нумикон в данном случае очень удобен.
Вывод, к которому нужно прийти в своём исследовании, что в любом чётном числе прячутся полные пары, а любое нечётное имеет только один элемент без пары, и его соседи в числовом ряду оба будут чётные (либо одиночка ушёл, либо пару себе нашёл).
Есть! Понятие и представление о чётных числах есть.
Напоминаю, что автоматизированные ряды счета группами в прямой и обратной последовательности и в возрастающих и убывающих интервалах тоже есть.
Строим таблицу 10х10.
Выделяем диагональ квадратов числа (о чем мы точно узнаем сильно позже) от верхнего левого до нижнего правого угла (цветом или рамочкой).
Сначала заполняем только половину таблицы (диагональ = зеркальное отражение). И отражать от зеркала нужно сразу, работая с примерами-близнецами и с темой «Переместительный закон умножения».
Учим таблицу умножения на 1, раскладываем в пеналы карандаши:
В 1 пенал кладем 1 карандаш — сколько карандашей? Вписываем на пересечении 1шт х 1раз = 1
В 2 пенала кладем по 1 карандашу — сколько карандашей? Вписываем на пересечении 1шт х 2раза = 2
В 3 пенала кладем по 1 карандашу — сколько карандашей? Вписываем на пересечении 1шт х 3раза = 3
Если любое число умножить на 1 = это же число (15, 28, …)
Это очень важно! Нужно сразу показать юному исследователю числовой прямой его неограниченные возможности в умножении.
Есть жизнь за пределами таблицы Пифагора в 100 клеток. Любое число, взятое 1 раз, равно ему же
Может быть, человек ещё не умеет записать со слуха или прочитать «сорок две тысячи семьсот девяносто три», но решить пример 42793 × 1 может!
Это чудо и волшебство.
Между первым открытием и вторым никакого временного интервала.
Сразу учим таблицу умножения на 0.
В 1 пенал кладем 1 карандаш и прячем этот пенал — сколько карандашей? 0, мы не видим их, нет пенала 1шт х 0раз = 0. Вот оно новое открытие. Сколько бы ни хранились шоколадных конфет в коробке, если коробки нет, то жизнь боль и конфет нет.
Если любое число умножить на ноль, то получится 0 (если положить любое число конфет, и не дать коробку — ничего не будет).
Вопрос может вызвать пример 1х0=0 (любой вариант решения — верный). То есть коробка с одной конфетой, и коробку не дали. Или одна коробка, в которой нет конфет. Результат, увы, одинаковый.
Любому волшебнику нужно три чуда, поэтому сразу учим таблицу умножения на 10.
Раскладываем в пеналы карандаши по 10шт, связанные резинкой:
В 1 пенал кладем 10 карандашей — сколько карандашей? Вписываем на пересечении 10шт х 1раз = 10
В 2 пенала кладем по 10 карандашей — сколько карандашей? Вписываем на пересечении 10шт х 2раза = 20
В 3 пенала кладем по 10 карандашей — сколько карандашей? Вписываем на пересечении 10шт х 3раза = 30
…
Если любое число умножить на 10, то нужно справа дописать справа 0.
Если уже введены понятия о разрядах и велась работа в разрядной таблице с цветными столбиками, можно научить этому фокусу с более глубоким пониманием.
Всё разряды сдвигаются на шаг влево, в разряде единиц 0. Число больше в 10 раз.
P.S. И по программе 8.2
Знать таблицу наизусть не обязательно, важно уметь пользоваться самостоятельно опорой и было бы неплохо понимать суть действия
Умножение на 9
Есть простой способ умножения числа 9. Даже не один. Самый простой базируется на знании состава числа 10. Чтобы узнать ответ умножения на 9, сначала умножим число на 10 (то есть добавим нолик), а затем вычтем это число. 6*9 = 6*10 — 6 = 60 — 6=54
С помощью пальцев. Положим свои руки на стол и мысленно пронумеруем пальчики слева направо от 1 до 10. Чтобы выполнить действие умножения, допустим 9*7= ?, загибаем седьмой слева пальчик. Ответ готов: оставшиеся не загнутыми пальчики слева образуют количество десятков в ответе, а не загнутые справа — количество единиц. Считаем, и говорим ответ: 63
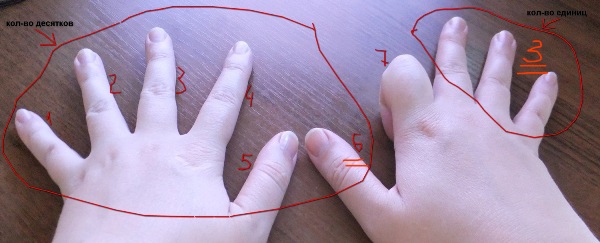
Второй способ. Рассмотрите таблицу умножения числа 9. Какую закономерность можно увидеть? Сумма чисел во всех произведениях равна 9! А теперь давайте разберемся, как узнать само произведение. Из второго множителя вычитаем 1 и получаем количество десятков в ответе. Чтобы узнать количество единиц, надо из 9 вычесть количество десятков. Попробуйте несколько раз, покажите эти способы ребенку, чтобы он мог ими пользоваться.
Способы запоминания таблицы умножения
Существует множество приемов и методов, при помощи которых можно запомнить информацию с первого раза. Это образные, игровые и логические способы работы с материалом, среди которых наиболее популярными считаются следующие.
Карточки
Карточки с яркими картинками – один из самых известных приемов, как легко и быстро освоить таблицу умножения. Предварительно готовится набор карточек с примером умножения без ответа (8х8=?). Суть игры состоит в том, что ребенок вытягивает из стопки карточку и озвучивает получаемое при умножении число. Если ответ правильный, карточка «выходит» из игры, а если неверный – возвращается в общую стопку. Игра продолжается до тех пор, пока не закончатся все карточки и не будут даны правильные ответы на все примеры.
Конечно, на первых порах лучше использовать карточки с умножением только на несколько чисел, например, на 2 и 3. После того как ребенок усвоит простые вычисления, переходите к цифрам посложнее: умножению на 4 и 6, затем – на 7 и 9. Материал можно взять с подходящего интернет-ресурса и распечатать, но лучше сделать карточки вместе с ребенком, нарисовав его любимых мультипликационных героев или персонажей сказок.
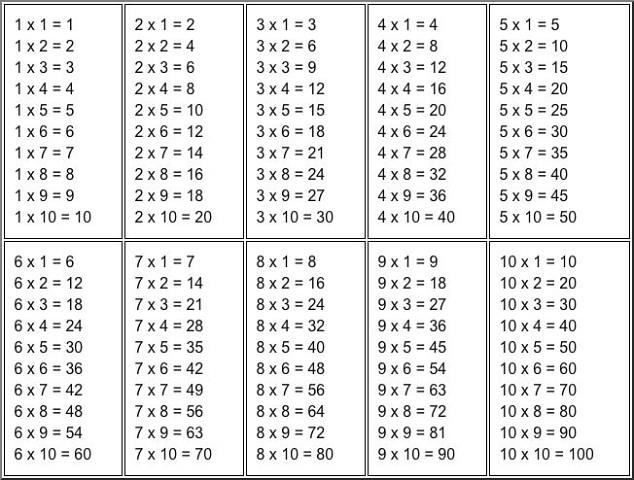
На пальцах
Пальцы рук – безошибочный счетчик, если правильно научить ребенка ими пользоваться. Для начала нужно пронумеровать пальцы как на картинке, – присвоим им цифры от 6 до 10.
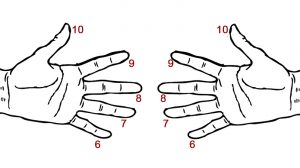
Нумерация пальцев рук
Попробуем перемножить 7 и 8, используя пальцы. Для этого нужно соединить седьмой палец на левой руке и восьмой палец – на правой, провести мысленно над ними черту и посчитать количество пальцев сверху и снизу на каждой руке. Остается только сложить количество нижних пальцев между собой, и определить десятки – 3+2=5 десятков. Затем перемножить между собой количество верхних пальцев между собой и получить единицы – 2х3=6 единиц. В результате получается 56.
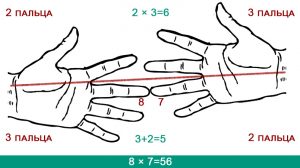
Умножение 7х8 с помощью пальцев рук
Немного по-другому проводят умножение на 9. Для этого нужно пронумеровать пальцы рук, начиная с единицы. Если нужно умножить 6х9, нужно согнуть шестой палец и посчитать количество пальцев слева до него, обозначающих десятки – 5. Затем посчитать количество пальцев справа от загнутого пальца, обозначающих единицы – 4. Получится 54.
Умножение с помощью пальцев рук на «9»
В стихах

Книга Александра Усачева
Детям с гуманитарным складом ума будет легче запомнить таблицу умножения в стихотворной форме. Приобретите для ребенка книгу Марины Казариной или Александра Усачева с веселыми стихами, которые не только развлекут, но и помогут постичь азы умножения. Для каждого примера из таблицы авторы придумали короткие двустишья или четверостишья, которые легко запоминаются даже дошкольниками.
Песня
Некоторые примеры из таблицы умножения легко выучить с помощью песни композитора Владимира Шаинского на слова Михаила Пляцковского «Дважды два – четыре». Заводная мелодия поднимает настроение, а строчки из песни легко запоминаются даже маленькими детьми.
Мультфильмы
Все дети любят мультфильмы! В интернет-сети можно найти как российские, так зарубежные развивающие мультипликационные фильмы, помогающие изучить азы умножения. Сделайте для ребенка подборку с любимыми героями, чтобы процесс обучения стал интересным, веселым и увлекательным.
Таблица Пифагора
Необязательно учить классические столбики с примерами! Существует более простой способ умножения чисел – таблица Пифагора. В ней количество сочетаний сокращено до 36. Правило умножения простое: выбирается число в левом столбике и умножается на цифру из верхней строки. Ответ находится на месте их пересечения.
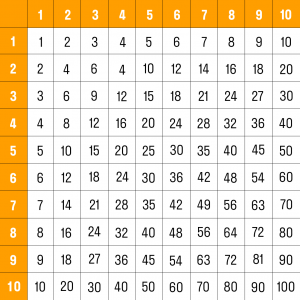
Таблица Пифагора
Если ребенок утомился, старайтесь не останавливаться во время выполнения упражнения до тех пор, пока не наступит улучшение или показатель не повысится по сравнению с исходным. Переключайте деятельность только между заданиями, иначе ребенок привыкнет отступать при первой же неудаче. Если малыш сомневается в своих силах, попросите его не расстраиваться, уточните, что именно вызвало затруднения, мягко предложите перемножить числа еще раз.
Таблица степеней 🆕
Бесплатный вводный урок по математике
Записаться
После изучения арифметических основ в виде сложения, вычитания, деления и умножения, открывается математика и ее большой мир. В этом материале рассмотрим такое понятие, как степень.
Основные понятия
Степень числа с натуральным показателем — это результат многократного умножения числа на себя. Само число называют основанием степени, а количество операций умножения — показателем степени.
- an = a × a × … × a, где a — основание степени,
- n — натуральный показатель степени.
Запись читается, как «a» в степени «n».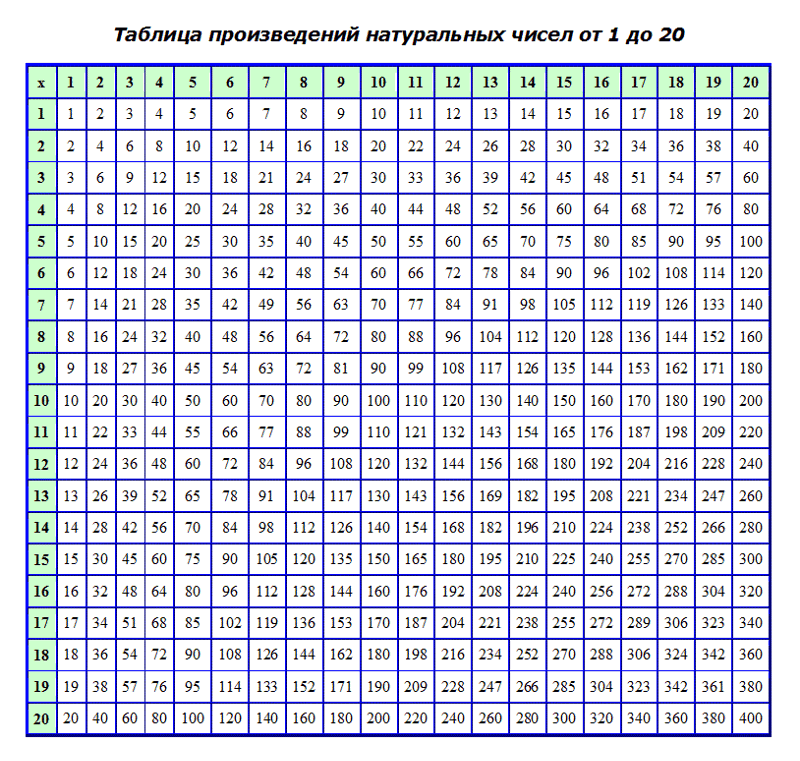
Вот пример для наглядности:
35 = 3 × 3 × 3 × 3 × 3 = 243
Эту запись можно прочитать тремя способами:
- 3 в 5 степени;
- пятая степень числа три;
- возвести число три в пятую степень.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Свойства степеней
Свойства степеней обычно используют, чтобы сократить или упростить сложные примеры. Удобно использовать вместе с таблицей степеней и таблицей умножения.
|
a1 = а a = 1 (a ≠ 0) a−n = 1 : an am × an = am+n am : an = am-n (a × b)n = an × bn (am)n = am×n (a : b)n = an : bn |
Подготовка к ЕГЭ по математике онлайн поможет снять стресс перед экзаменом и повысит шансы на высокий балл.![]()
Таблица степеней от 1 до 10
Таблица степеней — это перечень чисел от 1 до 10, возведенных в степень от 1 до 10. Ниже приведены два вида таблиц: выберите ту, которая удобнее для вас, скачайте на телефон или распечатайте и положите в учебник.
Как найти необходимые значения в этой таблице:
- В первом столбце находим число, которое обозначает степень. Запомним номер этой строки.
- В первой строке находим показатель степени. Запомним найденный столбец.
- На пересечении строки и столбца находится ответ.
В этой табличке мы просто ищем нужное нам число в степени и получаем ответ.
А если ответ нужно получить как можно быстрее, можно использовать онлайн-калькулятор степеней.
Решение задач
Задание 1. Упростить и решить выражение 5
2 × 53.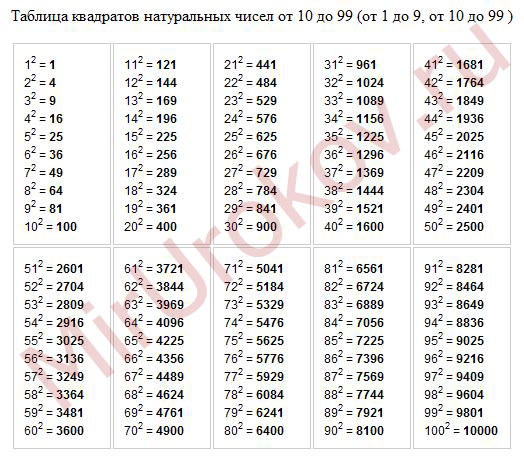
Как решаем:
52 × 53 = 52+3 = 55 = 3125
Задание 2. Упростить и решить выражение 24 × 33 × 25.
Как решаем:
24 × 33 × 25 = 24+5 × 33 = 29 × 33 = 512 × 27 = 13 824
Задание 3. Найти 364.
Как решаем:
При условии, что у нас есть только таблица до 10, разложим основание степени на множители:
364 = 64 × 64 = 1296 × 1296 = 1 679 616
364 = 64 × 64 = 6 8 = 1 679 616
Шпаргалки по математике родителей
Все формулы по математике под рукой
Используйте закономерности таблицы
Очень важно, чтобы ребенок не занимался простым механическим заучиванием, а понимал смысл выполнения умножения. Рекомендуем для понимания физического смысла, использовать следующий метод:
- Разделите таблицу на прямоугольники, каждая сторона которых соответствует цифрам, которые будете умножать друг на друга.
- Выделите первые клеточки – 2х4, обведите их красным маркером.
- Сосчитайте, сколько клеток совмещается внутри одного полученного прямоугольника. Так вы поймете, что количество клеток – 8.
Это работает, если обвести любое количество цифр и сложить их между собой. Физический смысл умножения кроется именно в этом.
Еще одно важное понимание заключается в том, что в таблице есть закономерности. Это значительно ускоряет изучение
Среди главных закономерностей есть следующие:
- Любая цифра останется прежней, если умножить ее на 1.
- При умножении на 2 к цифре прибавляется еще одна такая же.
- При любом умножении на 5 получается число, в конце которого стоит либо 5 либо 0.
- Если умножать на 9, то сумма всех чисел полученного результата будет также 9.
- Умножение на 10 самое простое – достаточно просто приписать к числу 0.
Все это показывает ребенку, что в математике есть много закономерностей и главное – научиться ими правильно пользоваться, чтобы быстро решать практически любые примеры.
 Изучение классической таблицы умножения занимает больше времени, чем варианта Пифагора.
Изучение классической таблицы умножения занимает больше времени, чем варианта Пифагора.
Понять суть умножения
После того, как заложена база, важно понять суть умножения.
Для этого нам необходимы:
• Одинаковые коробки или пеналы -10 шт (пеналы в виде пластиковых тубусов);
• Много незаточенных карандашей — 100 шт;
• Коробки из-под яиц;
• Яйца от киндер сюрпризов;
• Любые идентичные ёмкости и множество.
• Множество чего?
Вопрос: сколько тут карандашей?
Ответ (вариант 1): 1+1+1+1+1+1+1+1+1+1=10 (это очень долго).
Ответ (вариант 2): 2+2+2+2+2=10 (это быстрее).
ОЧЕНЬ ВАЖНО, что к выводу о том, что считать группами быстрее, ребёнок должен прийти сам. Для этого у него в быту или в игре уже должен быть продолжительный опыт (см
Все игры и задания с делением целого).
Ответ (вариант 1): 1+1+1+…+1=15 (это очень долго).
Ответ (вариант 2): 3+3+3+3+3=15 (это быстрее).
Умножение быстрее, чем сложение.
Рассмотрев на карандашах и других предметах, можно переносить на схематичное, условное или символически обозначение на карточках, и т.д.
Как запоминать таблицы умножения [с подсказками зрительной памяти]
Математика
По Джен Уинтерс
Когда дело доходит до изучения таблицы умножения, стандартный способ преподавания этого предмета состоит в том, чтобы использовать механическое заучивание для быстрого запоминания математических фактов.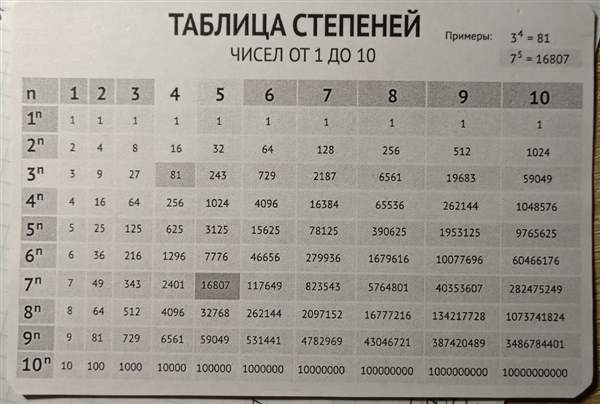
настолько эффективно без особых усилий повторять заглавные буквы таблицы умножения
Раскрытие информации: этот пост был написан членом команды Trigger Memory — основателями Times Tales, Pet Math и Kids Chore Chart.
Когда мы обычно думаем об умножении, мы представляем себе набор чисел на сетке.![]()
запоминание ключа t
Сила мнемотехники!
Существует новый способ запоминания фактов старшего умножения с помощью системы, использующей мнемонику для запоминания. Для тех, кто не знаком с мнемоникой, в самых простых терминах это «привязка» памяти, которая заставляет мозг что-то вспомнить. Например, когда вы встречаете кого-то нового, вы связываете его имя с кем-то, чье имя вы уже знаете, например, с вашим соседом Джо. Когда ты увидишь новый Джо, вы изобразили старого соседа Джо вместе с ним.
Так какое отношение старый сосед Джо имеет к таблицам умножения?
Оба Джо могут быть сохранены в банке памяти, который не настроен на удаление сразу после сохранения информации. Как только вы объединяете математические факты с правым полушарием мозга, визуальными эффектами и привязываете историю к числам (с небольшим количеством эмоций по поводу этой истории), этот математический факт сохраняется в памяти на неопределенное время. Это как магия умножения!
Times Tales — это один из новых способов, с помощью которых школы обучают таблице умножения с помощью системы мнемонического запоминания. Многие учителя, которые перешли от механического заучивания к мнемоническому заучиванию , обнаружили, что время в классе, традиционно затрачиваемое учащимися на изучение таблицы умножения, сокращается до дроби .
Изучение таблиц умножения в течение многих лет было тем, что мы бы назвали обучением левого полушария, таким как: обработка чисел, аналитическое мышление и язык.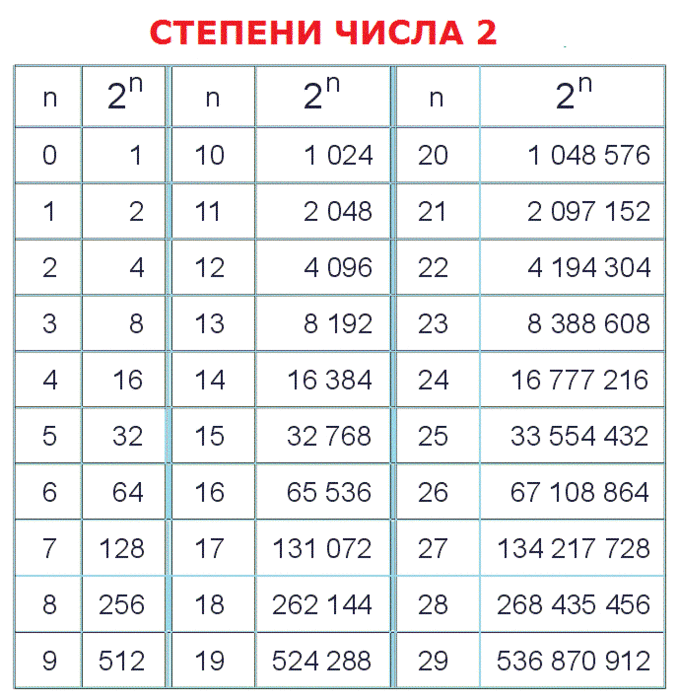
Times Tales работает в школах
Этот мнемонический метод изучения таблицы умножения оказался настолько эффективным, что многие школы в США переходят на этот способ обучения своему классу таблице умножения. Узнайте больше о школьных изданиях Times Tales.
Multiplication_Chart_Drills_Printables
Закрепить!
Первые шаги в изучении таблицы: самые легкие числа и освоение принципа
Как помочь выучить таблицу умножения? Обучение ребенка таблице умножения должно происходить по определенному плану. Маме или папе следует составить индивидуальную программу изучения таблицы для своего ребенка: наиболее рационально было бы начать занятия с самых легких примеров, на них необходимо объяснить суть действия умножения, то есть, что первое число необходимо прибавить столько раз, сколько указано во втором числе, и то, что можно менять эти числа местами — результат будет тот же. После того, как малыш поймет смысл умножения, запоминание будет происходить быстрее и проще. При этом не следует сразу нагружать малыша информацией о делении, о взаимосвязи этих двух действий, это можно отложить на более позднее время.
Необходимо разъяснить ребенку, что между первым и вторым множителем может стоять точка либо диагональный крестик, и оба знака обозначают действие «умножить».
Обратите внимание! Педагоги советуют сразу знакомить школьников с профессиональной терминологией, то есть после объяснения базовых принципов следует показать на множестве примеров, что такое множитель и произведение. Если не упоминать данные понятия во время обучения в летние каникулы, то в сентябре во время первых уроков и проверки заданий на лето такие термины могут сбить ребенка с толку
Как легко и быстро помочь ребенку выучить таблицу умножения наизусть
Сначала ребенок должен запомнить, что:
- При умножении на 1 любое число останется прежним.
- Если один из множителей — 5, то искомое число всегда будет заканчиваться на 0 или 5.
- Четное число 4 можно заменить двойным умножением на 2.
Помните, что умножение можно заменить сложением (4х3=4+4+4=12).
Еще одно правило, облегчающее умножение:
И самое важное правило: при перестановке умножаемых друг на друга чисел местами результат не изменится
Заниматься с ребенком математикой нужно регулярно, желательно повторять пройденный материал несколько раз. Не нужно принуждать школьника к занятиям: его должен заинтересовать сам процесс. Лучший метод запоминания — это игровой. Играючи, детки не замечают, что их обучают.
Продолжаем осваивать и составлять таблицу Пифагора
Если ребёнок может считать двойками, то есть знает ряд чётных чисел, то он знает таблицу на 2, 4, 6, 8. Главное научить прыгать разными интервалами и показать, что одинаковые числа есть в разных столбцах. Чётные числа очень пригодятся, для того чтобы показать признаки деления на пять. Десяток, полдесятка.
Если пятёрки брать чётное количество раз, то это тоже самое, что брать десятки по количеству пар (чёт) в числе. 5*6. Быстренько парами считаем: 2, 4, 6. Три пары, значит 3 десятка.
Самые интересные открытия можно делать в ряду 9. Кроме того, что это основной пример умножения на пальцах, ещё очень интересно наблюдать, что количество десятков в числе на 1 меньше, чем количество раз, которое мы берём число. А количество единиц дополняет это значение до 9.
9*2=18 1 меньше, чем 2 на 1, 1+8=9
9*3=27 2 меньше, чем 3 на 1, 2+7=9…
Таблица на 3: о чудо!
При умножении на чётные значения совпадают с таблицей на 6.
Самая заковыристый столбец — это семёрка.
Обязательно нужно показать, что диагональ квадратов числа делит таблицу как зеркало. Сразу можно показать переместительный закон умножения. Для детей, которым сложно следить за столбом и строкой можно использовать тве полоски из полупрозрачной плёнки разных цветов, например красную и зелёную. Красная — на столбцы, зелёная — на строки. Точка пересечения — это произведение. Полоски можно подписать: «первый множитель» и «второй множитель». Ребёнок выполняет двумя руками действие перемещение множителей. Можно использовать разные игры с помощью прозрачных окошек. Найди в столбце умножения на 3, такие же числа, которые есть в столбце на 6.
После выполнения всех шагов необходимо закреплять навык использования самостоятельно созданной таблицы при решении бытовых задач.
Отлично подходят игры в лото, когда на пример накладывается ответ, и наоборот.
Можно при закреплении темы про примеры-братья сделать лото с обратным выражениями. По этому же принципу подойдёт и домино, и мемори.
Обязательно нужно закреплять навык применяя умножение в магазине, в вопросах, связанных с временными интервалами. Одну страницу я читаю за 5 минут, сколько потребуется времени, чтобы прочитать 5 страниц?
Нет предела совершенству, но с этой темой закругляемся!
Психотипы детей: кто и как запоминает
Просматривая варианты методик, как легко и быстро выучить таблицу умножения, сначала определяют психотип ребенка. Люди разные, информацию воспринимают и запоминают проговариванием, записыванием или внимательным просмотром. В зависимости от восприятия выбирают тип обучения первоклассника.

Различают следующие психотипы:
- Аудиалы. Это люди, которые запоминают услышанное. Песенки, стишки, разговоры – способы, как можно быстро выучить таблицу умножения с аудиалом.
- Визуалы. Им проще видеть яркие образы. Помогут раскраски в виде буквенного изображения или цифр. Визуальное восприятие подкрепляют рисунками, мультфильмами, в работу задействуют образное мышление.
- Киненстетики. Таким детям нужны тактильные ощущения. Для обучения готовят карточки, кубики с числами, чтобы ребенок их перемещал, складывал.
Учим таблицу умножения: лайфхаки и видео
Важно понять, как ребенку комфортнее воспринимать информацию, чтобы процесс не превратился в «зубрежку». Все очень просто:. Дети-аудиалы
лучше учатся новому в разговоре
Им нравится заучивать цифры, повторяя примеры вслух. Хороший вариант запомнить таблицу умножения — разучивать стихи, песенки или смотреть обучающие видео
Дети-аудиалы
лучше учатся новому в разговоре. Им нравится заучивать цифры, повторяя примеры вслух. Хороший вариант запомнить таблицу умножения — разучивать стихи, песенки или смотреть обучающие видео.
Учим таблицу умножения (видео)
Ребенок-визуал
легче обучается, если задействованы зрение и образы. Они усваивают информацию с помощью ярких рисунков, игр-раскрасок, в которых есть крупные цветные шрифты и цифры.
Таблица умножения игра-раскраска (картинка)
Также с ребенком-визуалом можно смотреть обучающие мультфильмы, в которых любимые персонажи выступают в роли учителя.
Таблица умножения на 9
с Фиксиками (видео)
Дети-кинестетики
учатся через ощущения и чувства, которые у них возникают при контакте с новым предметом и информацией. В этом случае можно попробовать метод карточек.
Учим таблицу умножения с помощью карточек (видео)
Важно учитывать, как ваш ребенок лучше всего обучается, тогда процесс заучивания таблицы умножения пройдет весело и легко
План изучения таблицы
Самые простые столбцы таблицы можно учить по 1-2 дня, к более трудным необходимо подойти основательнее. Наиболее рациональной представляется следующая последовательность изучения таблицы:
- Итак, начать обучение следует с единицы и десятки. Достаточно объяснить ребенку, что какое-то число берется один раз — ответом является изначальное число, а при умножении на 10 — достаточно дописать ноль к первому множителю.
- Следующий этап — цифра 2. Поскольку школьник уже умеет складывать числа, следует объяснить, что для умножения числа на 2 нужно лишь сложить значение первого числа с ним же.
- Значения таблицы у еще одного несложного множителя — 4 — проще понять, когда малыш усвоит, что произведение можно получить при помощи повторного умножения на 2, т. е. здесь также нет необходимости заучивать.
- Для того чтобы научить малыша умножению на цифру 3, можно использовать вспомогательные средства, поскольку данный множитель не имеет секретных и легко запоминающихся приемов. Поспособствовать могут стихи, ассоциации с окружающими предметами.
- Изучение цифры 5 не должно вызвать особенных затруднений. Выучить просто — при умножении на четное число произведение заканчивается на ноль, на нечетное — вторая цифра в ответе будет 5.
- Умножение на 9 также нетрудно запомнить, поскольку существует техника, облегчающая этот процесс, — необходимо вытянуть перед собой руки ладонями вверх, представить порядковые номера пальцев слева направо. Когда будет назван второй множитель, нужно согнуть соответствующий палец, и количество пальцев слева будет означать первую цифру полученного произведения, а пальцы справа — вторую цифру. Помочь школьнику с умножением на 9 также может знание факта, что сумма чисел в произведении всегда равна 9. Так, если он помнит, что при умножении на 4 первая цифра в произведении — 3, то вторая = 9 – 3 = 6, ответ: 36.
Для того чтобы упростить запоминание умножения на цифру 9, можно раскрыть математический секрет — необычное сочетание значений умножения в столбце произведения.
Умножение на 9
- Столбики произведения на 6, 7 и 8 придется заучить, хотя многие значения ребёнку будут известны благодаря уже изученному материалу. Для общего развития можно показать школьнику принцип умножения на число 11.






























